当前位置：首页 > news >正文

【题解-Acwing】798. 差分矩阵

news 来源：原创 2025/5/18 7:20:28

题目：798. 差分矩阵

题目描述

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1)和 (x2,y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入

第一行包含整数 n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数 x1,y1,x2,y2,c，表示一个操作。

输出

共n行，每行m个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

时空限制

2s / 64MB

代码

#include<iostream>

using namespace std;

const int MaxNM = 1010;

int n,m,q;
int a[MaxNM][MaxNM];
int b[MaxNM][MaxNM];

void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;
}

int main(){
    scanf("%d%d%d", &n,&m,&q);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d", &a[i][j]);
            insert(i, j, i, j, a[i][j]);
        }
    }
    while(q--){
        int x1,y1,x2,y2,c;
        scanf("%d%d%d%d%d", &x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];
            printf("%d ",b[i][j]);
        }
        printf("\n");
    }
    return 0;
}

结果

在这里插入图片描述

解析

差分这块重点在于利用差分求前缀和从而实现原矩阵的区间值的改变。首先，我们来看差分矩阵中区间值得修改操作原理。

1、差分矩阵值的修改

如图（表示的是差分矩阵，每个格子表示一个数）。要实现对红色块区域+c（c为一个常数）。
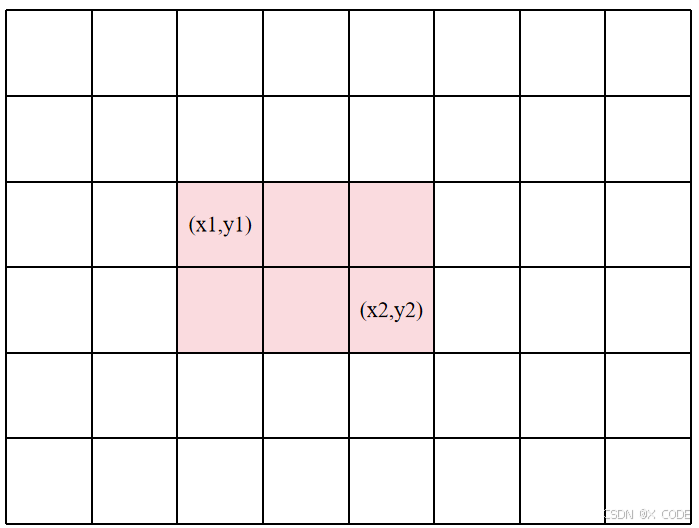
在这里插入图片描述
需要将b[x1][y1]+c，这样会使得蓝框的值都改变，因此，还需要将绿色斜线和橙色斜线部分的值-c，并将绿色斜线和橙色斜线重叠部分的值+c。

根据差分的原理，接下去，可以用差分矩阵来表示。