因果推断【Causal Inference】（一）

---

1. 什么是因果推断？

所谓因果推断，就是寻找变量间的因果关系，并估计由于因对果造成的效应大小。
它之所以重要，是因为因果关系一旦被准确衡量，那么只要控制了原因，我们就能得到想要的结果。

---

2. 为什么要提出因果推断？Motivation：辛普森悖论

先来看一个非常经典的例子，假设今天出现了一个新的病毒COVID-27，现在有两种治疗方案：A和B，其中 B 比 A 更稀缺（耗费的医疗资源更多），应该选择哪种方案才能尽量减少死亡？

现在有一组实验数据，分别对 轻症(Mild) 和 重症(Severe) 患者给予两种治疗，其结果如下图所示。

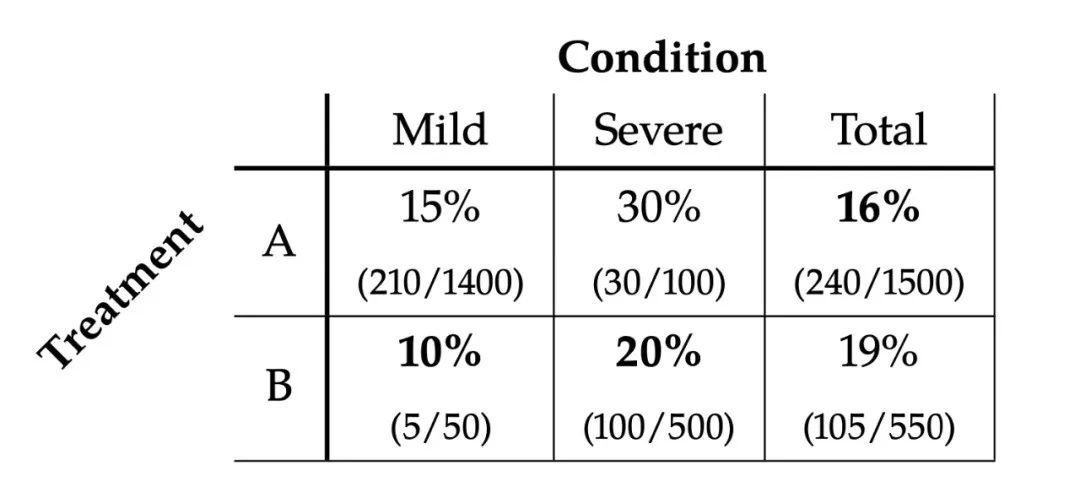
• 对于方案A：15%的轻症病人死亡，30%的重症病人死亡，总死亡率为16%.
• 对于方案B：10%的轻症病人死亡，20%的重症病人死亡，总死亡率为19%.

我们应该选择哪个方案对整个国家的人进行治疗呢？

明显的悖论源于这样一个事实：从总死亡率来说，方案A的死亡率更低（16%<19%），应该选择方案A。但是，从轻度和重度两个组来看，方案B的死亡率都更低（15%>10%，30%>20%），应该选择方案B。
这就是辛普森悖论，从轻度和重度两个视角看，方案B的死亡率都是更低的，然而其总死亡率却高于方案A。

出现辛普森悖论的关键因素是各个类别的非均匀性。
接受方案A治疗的1500人中有1400人是轻症病人，而接受方案B治疗的550人中有500人是重症病人，即方案A治疗的大部分都是轻症病人，而方案B治疗的大部分是重症病人，因为轻症病人的死亡可能性本来就比较小，所以方案A的总死亡率更低。

其次，方案A和方案B都有可能是正确答案，这取决于数据的因果结构。换句话说，因果关系是解决辛普森悖论的关键。

下面首先从从直觉上给出什么时候应该偏向于方案 A，什么时候应该偏向于方案 B。

Scenario 1

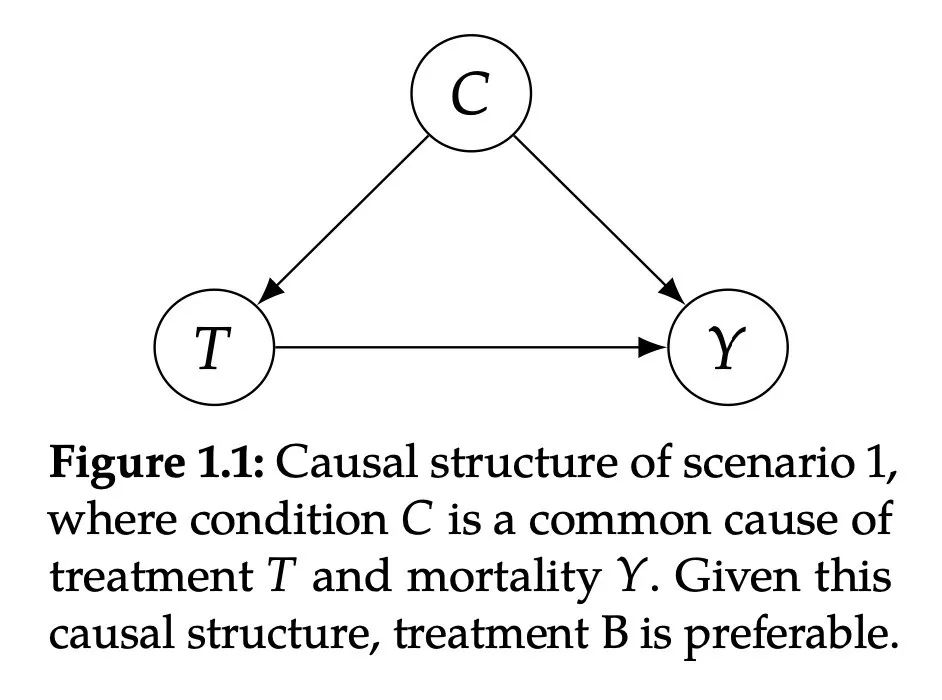
如图所示，其中 C (Condition) 代表病情轻重，T (Treatment) 代表治疗方案，Y (outcome) 代表是否死亡。C是T和Y的共同原因。 即，病情轻重C会影响选择哪种治疗方案T，并且病情轻重C也会导致是否死亡Y。

在这种情况下，医生会给大多数病情轻微的人提供方案A，而对病情较严重的人使用方案B治疗。因为病情严重的人更有可能死亡(C→Y)，并且病情严重更有可能接收方案B治疗(C→T)。

因此，方案B的总体死亡率更高的原因是因为选择方案B中的人大多数（500/550）是重症，即使选了方案B其死亡率100/500=20%也比轻症用方案B的死亡率5/50=10%要高，最终混合的总结果会更偏向于重症的结果。

在这里，病情 C 混淆了治疗 T 对死亡率 Y 的影响。为了纠正这种混杂因素，我们必须研究相同条件的病人的 T 和 Y 的关系。这意味着，最好的治疗方法是在每个子群体（图中的“mild”和“severe”列）中选择低死亡率的治疗方法：即方案 B。

Scenario 2

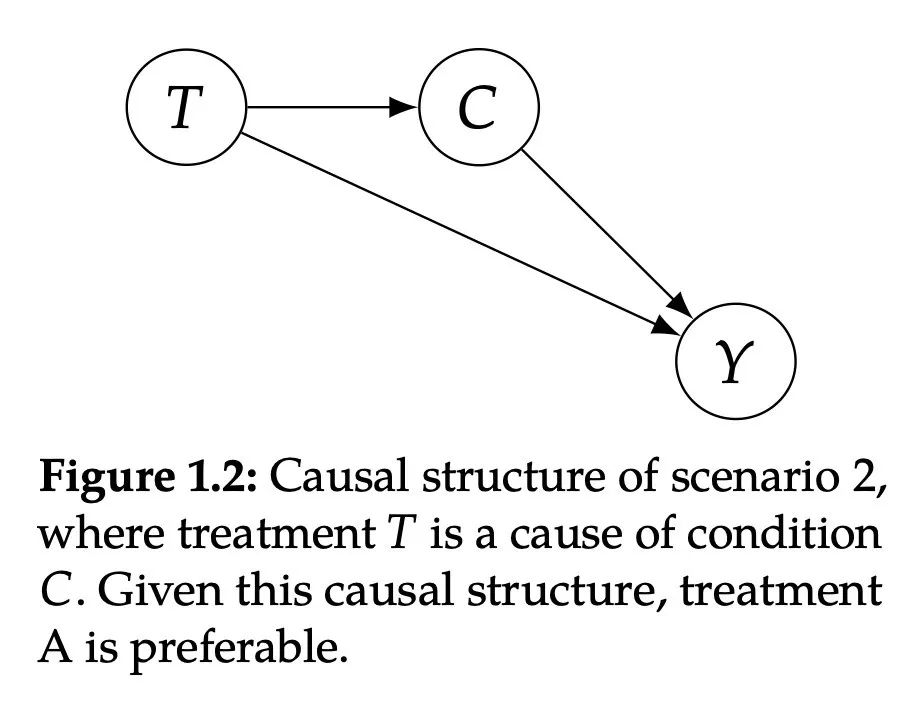
T是C的原因，而C又是Y的原因。即治疗方案T是病情轻重C的原因，而病情轻重C又是是否死亡Y的原因。

这种情况的实际场景是，方案B非常稀缺，需要病人在被开出治疗处方之后，等待很长时间才能接受治疗，而选择方案A的患者则不存在这个问题。

因为COVID-27患者的病情会随着时间的推移而恶化，开出治疗B实际上会使病情轻微的患者发展为严重的病情，造成更高的死亡率。因此，即使方案B一旦用药就比方案A更有效（正面作用T→Y），由于选择方案B会导致病情恶化（因为等待时间更长，负面作用T→C→Y），因此方案B总的来说效果较差。考虑到这种因果结构，方案A是比较好的。

总之，更有效的方案完全取决于问题的因果结构。

---

3. 【Note】相关性≠因果

在平时使用的机器学习模型中，得到的估计结果反映的是变量间的相关性。然而，相关并不意味着因果（Correlation does not Imply Causation）。

事实上，因果关系只是相关关系的一种。除了因果(Causation)，相关性的主要来源还有 混淆(Confounding) 和 样本选择偏差(Selection bias) 。三类分别对应以下三种结构：

下面通过一个例子来直观地理解相关性≠因果的含义。

3.1 混淆(Confounding)——共同原因

混淆(Confounding)是指存在一个变量 $X$（混淆因子），该变量构成了 $T$ 和 $Y$ 的共同原因；如果忽略了 $X$ 的影响，那么 $T$ 和 $Y$ 之间就存在假性相关关系：即 $T$ 并非 $Y$ 产生的直接原因。

【E.g.】例如：在夏天，由于天气热，所以买雪糕的人多；同样地，由于天气热，游泳溺水的人数增加。如果忽略了气温的影响，仅凭冰激凌销量与溺水人数呈现出来的正向相关关系，则可能会得出吃冰淇淋会导致游泳溺水的错误结论。

3.2 样本选择偏差(Selection Bias)——共同结果

样本选择偏差(Selection Bias)是指，当两个相互独立的变量 $T$ 和 $Y$ 产生了一个共同结果变量 $S$ （对撞因子），引入 $S$ 则为 $T$ 和 $Y$ 之间打开了一条通路 $T\to S\leftarrow Y$，从而误以为 $T$ 和 $Y$ 之间存在关联关系，以共同结果为条件造成估计结果的偏差，这种现象也被称为“伯克森悖论”。

伯克森悖论揭示了一个现象：样本的选择会导致因果分析的误差。

【E.g.】例如，在一项研究中发现，一般人群中大约有5%的肩周炎，这一比例与眼镜度数无关。但是当只关注过去3个月患肩周炎的患者时，发现患有肩周炎，其眼镜度数平均提升250度，两者之间有很强的相关性。这是因为在研究时可能限制了对象都是一些平时用电脑较多的患者，因此他们用眼过度，导致眼镜度数增加。

---

4. 潜在结果(Potential Outcome)

潜在结果可以理解为，在每一种干预下可能的结果，任何一个干预都存在一个潜在结果。

场景1：一个人头疼，考虑是否吃药来帮助缓解头疼。如果吃药后头疼好了，是否意味着吃药能够治愈头疼？假设没有吃药头疼也会好怎么办？在这种情况下，吃药并不是头疼治愈所必需的，所以吃药能治好头疼的因果关系的说法是站不住脚的。

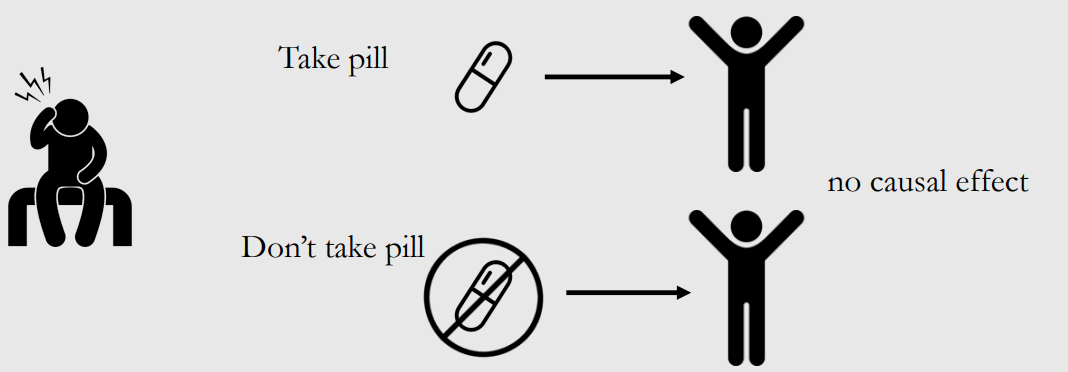
场景2：稍微改变一下，如果吃药后头疼好了，没有吃药仍然头疼，在这种情况下，吃药对头疼缓解有因果关系。

在上述两种情况下，都使用了称为潜在结果的因果概念。治疗 $T$ 代表是否吃药：$T=1$ 代表吃药，$T=0$ 代表不吃药；结果 $Y$ 代表是否头疼，$Y=1$ 代表不头疼，$Y=0$ 代表头疼。

• $do(T=i)$ 代表进行某种干预
• $Y_i(1)$ 表示吃药后的潜在结果；$Y_i(0)$ 表示没有吃药后的潜在结果
• $Y_i(1)-Y_i(0)$ 表示个人因果效应(Casual Effect)

补充概念：

• 单元（Unit）：干预作用的最小单元，可以是乘客、订单、时间片等，一个单元可以视为数据集中的一个样本点。
• 干预（Treatment）：作用于Unit的动作，假设投放广告、优化策略等；干预可以是二元，也可以是多元，例如多个实验室有不同的干预水平。
• 事实结果（Factual Outcome）：实际实施某种干预后所观测到的结果，也称为观测结果，是潜在结果的一种实际表现。
• 反事实结果（Counterfactual Outcome）：对于一个单元来说，除了它被实施的干预以外，其他所有干预的潜在结果都是反事实结果。

在场景1中：casual effect=1-1=0，在场景2中：casual effect=1-0=1。

然而，在实际场景中，我们只能得到一个干预后的潜在结果，因为我们不能同时让一个人吃药又不吃药。例如，一个人吃药了，那么无法观测到未吃药的反事实结果。而某一个单位的反事实结果是不能直接得到的。对于这种情况，就需要考虑一个群体的因果效应。

$$\text{Average Treatment Effect (ATE)}:E(Y_i(1)-Y_i(0))=E(Y(1))-E(Y(0))$$

想要直接得到 $E(Y(1))$ 不好计算，那能通过条件期望 $E(Y|T=1)-E(Y|T=0)$得到吗？答案是否定的。因为在很多情况下，这两个是不相等的，还记得嘛：相关性不等于因果。

当存在一个混淆变量 $C$ 时，$C$ 会对 $T$ 有影响。如果能够得到一个随机控制实验，使得 $C$ 与 $T$ 无关，则上述两个等式是相等的。

我们可以得到随机实验，使得控制组和对照组之间是可比的。但是在实际中，某些情况无法做随机实验，我们就只能使用观测数据来进行因果推断。

---

5. 观测数据下的因果推断

虽然AB随机试验是评估因果效应最科学的方法之一，但是在一些实际情况中，AB实验并不适用，例如：

• 样本之间存在一些关系
  • 样本之间存在社交网络关系（营销策略）
  • 样本之间存在竞争观察（分单策略）
• 样本被稀释（例如发券策略）
• 不存在可以分开的样本
  • 例如双十一，无法干预哪些用户参与，哪些用户不参与，这个时候就无法将用户分流
• …

那么如何根据观测数据来估计因果效应呢？这里先介绍一个最简单的方法。

假设有一个变量 $W$，它能够充分控制混淆(Confounding)，使得当给定 $W=w$ 时，$E(Y(t)\mid W=w)=E(Y\mid T=t,W=w)$，也就是说通过这个 $W$，阻断了其他变量对 $T$ 的影响，此时就只有 $Y$ 和 $T$ 之间的关系，因此我们可以得到：

这样就可以测量不同干预下潜在结果的期望。回到一开始的例子，此时 $C$ 相当于 $W$，根据上面的公式，可以计算结果如下：

从直觉上来看，此时在给定 $C$ 的情况下，$C$ 即不是 $T$ 的因，也不是 $T$ 的果，因此我们要计算的应该是两种方案整体的治疗效果，因此，我们将两种病情的比例来作为权重，且两种方案权重应该一致，因为我们面对的就是整体对象！

---

References

1. 【动手学因果推断】(一)：因果推断入门
2. 万字因果推断入门：为什么要做因果推断？
3. 【因果推断】一因果图模型与选择偏差