当前位置：首页 > news >正文

10天速通强化学习-009--DDPG、SAC、TD3

news 来源：原创 2025/6/22 1:55:28

DDPG

deterministic policy gradient theorem - 确定性

在线策略：TRPO 和 PPO

(样本效率高)离线策略：DQN--动作空间离散化，无法精细控制

DDPG--解决连续空间的控制问题，直接输出具体的动作值，不是概率分布。

原理

先来理解一下公式

$\nabla_\theta J(\pi_\theta)=\mathbb{E}_{s\sim\nu^{\pi_\beta}} \begin{bmatrix} \nabla_\theta\mu_\theta(s)\nabla_aQ_\omega^\mu(s,a)|_{a=\mu_\theta(s)} \end{bmatrix}$

左边：

$\nabla_\theta J(\pi_\theta)$ ：表示策略（有参数定义的确定性策略）的期望回报关于参数的梯度，目标是通过梯度调整参数以最大化期望回报。

右边：

$\mathbb{E}_{s\sim\nu^{\pi_\beta}}$ ：对状态按照分布（由策略和行为策略决定的状态分布）求期望

$\nabla_\theta\mu_\theta(s)$ ：确定性策略（输入状态，输出动作）关于参数的梯度

$\nabla_aQ_\omega^\mu(s,a)|_{a=\mu_\theta(s)}$ ：价值函数对动作的梯度（就相当于评估状态下动作的价值），这个动作是确定性策略输出的动作

整体：

通过在状态分布 v 下，对策略梯度（ $\nabla_\theta\mu_\theta(s)$ ）和 Q函数对动作的梯度（ $\nabla_aQ_\omega^\mu(s,a)|_{a=\mu_\theta(s)}$ ）的乘积求期望，得到参数 $\theta$ 的更新方向，从而引导策略向提升 Q 值得方向优化。

思考一下这个算法框架;

假设现在已经由函数Q，给定一个状态s，由于动作空间无线，无法通过遍历所有动作来得到Q值最大的动作，因此想用策略u 找到 Q 最大的动作 a ，即： $\mu (s) = argmax_{a}Q(s,a)$ 。

所以说 Q是 Critic , u是 Actor.

网络

包括四个网络，结合 DQN 使用目标网络（防止Q值波动），这就变成四个了，又使用double DQN （使用软更新）防止过高估计，还是四个。

Actor -- 策略网络

当前策略：输入当前状态 s ，通过网络计算输出当前状态下认为的最优动作 a ，用于与环境进行交互探索，其参数通常记为 θ 。

目标策略：结构与当前策略网络相同，参数记为 θ′ 。它以相对滞后、缓慢的方式更新（一般通过软更新，如 θ′←τθ+(1−τ)θ′ ，τ 是较小的更新系数）。主要作用是在计算目标 Q 值时，为目标 Critic 网络提供相对稳定的动作输入，减少训练过程中的波动，提高学习稳定性。

Critic - 价值评估网络

当前价值：输入状态 s 和动作 a ，评估该动作在当前状态下的价值，即输出 Q 值，反映从状态 s 执行动作 a 后能获得的期望累计回报，其参数记为 ω 。

目标价值：结构与当前价值网络相同，参数记为 ω′ ，同样采用软更新（如 ω′←τω+(1−τ)ω′ ）。在计算目标 Q 值时使用，依据贝尔曼方程，结合奖励 r 、下一状态 s′ 以及目标策略网络输出的动作来计算目标 Q 值，为当前价值网络的训练提供稳定的目标，辅助当前价值网络更好地收敛。

这里面有一个更新公式

$w^{-}\leftarrow \tau w+(1-\tau )w^{-}$

$\tau$ = 1 就是DQN的更新方式了， $\tau$ 很小的时候一次更新一点点

还有一点不同

探索方式引入噪声

伪代码

目标网络均采用软更新的方式来更新（最小化损失函数），策略网络使用梯度更新

随机噪声可以用 N 来表示，用随机的网络参数 ω 和 θ 分别初始化 Critic 网络 Qω(s,a) 和 Actor 网络 μθ(s)
复制相同的参数 ω−←ω 和 θ−←θ，分别初始化目标网络 Qω− 和 μθ−
初始化经验回放池 R
for 序列 e=1→E do:
- 初始化随机过程 N 用于动作探索
- 获取环境初始状态 s1
  - for 时间步 t=1→T do:
    - 根据当前策略和噪声选择动作
    - 执行动作 at，获得奖励 rt，环境状态变为 st+1
    - 将 (st,at,rt,st+1) 存储进回放池 R
    - 从 R 中采样 N 个元组 {(si,ai,ri,si+1)}i=1,…,N
    - 对每个元组，用目标网络计算
    - 最小化目标损失，以此更新当前 Critic 网络
    - 计算采样的策略梯度，以此更新当前 Actor 网络:
    - 更新目标网络:
- end for
end for

代码

以倒立摆环境为例

import random
import gym
import numpy as np
from tqdm import tqdm
import torch
from torch import nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils

四套神经网络，使用一层隐藏层的神经网络

PolicyNet类：
- 继承自torch.nn.Module，用于定义策略网络。
- __init__方法：初始化网络的结构，包括两个全连接层和动作最大值。
- forward方法：定义前向传播过程，将状态输入网络，输出一个在环境可接受范围内的动作。
QValueNet类：
- 继承自torch.nn.Module，用于定义 Q 值网络。
- __init__方法：初始化网络的结构，包括三个全连接层，输入维度为状态维度和动作维度之和。
- forward方法：定义前向传播过程，将状态和动作拼接后输入网络，输出对应的 Q 值。

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
        super(PolicyNet, self).__init__()
        # 定义第一个全连接层，将状态维度映射到隐藏层维度
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        # 定义第二个全连接层，将隐藏层维度映射到动作维度
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
        self.action_bound = action_bound  # action_bound是环境可以接受的动作最大值

    def forward(self, x):
        x = F.relu(self.fc1(x))
        # 通过第二个全连接层并使用tanh激活函数将输出限制在[-1, 1]之间
        # 再乘以动作最大值，将动作范围映射到环境可接受的范围
        return torch.tanh(self.fc2(x)) * self.action_bound


class QValueNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNet, self).__init__()
        # 定义第一个全连接层，输入维度为状态维度和动作维度之和
        self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
        # 定义第二个全连接层，将隐藏层维度映射到隐藏层维度
        self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
        # 定义输出层，将隐藏层维度映射到1维（Q值）
        self.fc_out = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x, a):
        cat = torch.cat([x, a], dim=1) # 拼接状态和动作
        x = F.relu(self.fc1(cat))
        x = F.relu(self.fc2(x))
        return self.fc_out(x)

接下来是主要部分，噪声项：使用正态分布的噪声

（有的地方使用OU随机过程噪声，特点是在均值附近做线性负反馈。）

class DDPG:
    ''' DDPG算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device):
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
        self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        # 初始化目标价值网络并设置和价值网络相同的参数
        self.target_critic.load_state_dict(self.critic.state_dict())
        # 初始化目标策略网络并设置和策略相同的参数
        self.target_actor.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
        self.gamma = gamma
        self.sigma = sigma  # 高斯噪声的标准差,均值直接设为0
        self.tau = tau  # 目标网络软更新参数
        self.action_dim = action_dim
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        action = self.actor(state).item()
        # 给动作添加噪声，增加探索
        action = action + self.sigma * np.random.randn(self.action_dim)
        return action

    def soft_update(self, net, target_net):
        for param_target, param in zip(target_net.parameters(), net.parameters()):
            param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)

        next_q_values = self.target_critic(next_states, self.target_actor(next_states))
        q_targets = rewards + self.gamma * next_q_values * (1 - dones)
        critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), q_targets))
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()

        actor_loss = -torch.mean(self.critic(states, self.actor(states)))
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        self.soft_update(self.actor, self.target_actor)  # 软更新策略网络
        self.soft_update(self.critic, self.target_critic)  # 软更新价值网络

倒立摆环境中训练

actor_lr = 3e-4
critic_lr = 3e-3
num_episodes = 200
hidden_dim = 64
gamma = 0.98
tau = 0.005  # 软更新参数
buffer_size = 10000
minimal_size = 1000
batch_size = 64
sigma = 0.01  # 高斯噪声标准差
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'Pendulum-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0]  # 动作最大值
agent = DDPG(state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device)

return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size)

结果

可视化

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()

学习速度快，样本数量少，训练波动大，对超参数敏感

总结

相较于DPG（确定性梯度算法）来说，加入了目标网络和软更新的方法，使得训练更稳定。

SAC

soft Actor-Critic,简单来说SAC就是一个既贪心（追求高回报）又好奇（探索新动作）的学习者

离线策略可以更好的使用样本，采样效率高。所以离线策略SAC出现了，特点---无模型，学习随机策略，无显式的策略函数，使用Actor 表示策略函数，求解连续空间的问题。

核心思想是通过引入熵正则化（Entropy Regularization）来平衡策略的探索与利用，同时结合 Actor-Critic 框架优化策略。

原理

熵（entropy）

对一个随机变量的随即程度的度量。

熵越大，变量的不确定性越高。这个公式

离散情况下等价于，十分重要。离散环境就是这样搞的

连续情况下求积分。

$H(\pi (.|s))$ ：表示策略 $\pi$ 在状态 s 下的随机程度

不难理解：注意有负号

最大熵强化学习：不仅最大化累计奖励，还要使得策略更加随机（避免陷入局部最优）.所以公式修改

左边：

优化后的最优策略

右边：最大化的期望

（利用-追求高奖励）第一项：对时间步上的即时奖励求和（并没有设计下一个状态，相当于一条序列的即时奖励算完），对环境奖励的最大化追求。

（探索-保持策略随机性）第二项：表示策略 $\pi$ 在状态 $S_{t}$ 下的熵，衡量随即程度，a 是权重参数（温度参数）---平均奖励和熵的贡献。熵最大，策略探索更多动作，避免陷入局部最优

讨论一个与算法无关的东西

为什么SAC要有soft这个词？

强调柔软也就是强调加入了熵，与硬不同（仅仅追求最大奖励，忽略探索的策略）
软更新网络

Soft 策略迭代

既然最终的策略也就是目标函数发生了变化，其他的变化也有，soft贝尔曼方程

这个又称为 soft Q函数

里面的状态价值函数发生了变化：

只看公式的左右两端

左边：状态价值函数

右边;

第一项：动作价值函数，之前的做法是到这里就截止了

第二项：策略 π 在状态 st 下动作分布的熵，衡量策略的随机性（熵越大，动作越随机，探索性越强）

之前介绍过KL散度，那么这里就用了在进行策略迭代的时候

左边：更新后的新策略

右边：使得（）里的KL散度最小，也就是概率分布最接近

第一项：待优化的新策略在状态 s 下的动作分布（策略提升得来的）

第二项：可以看作是由旧策略的Q值导出的分布（旧策略计算得来的）

准备工作做完了

SAC算法-网络

使用三个网络，两个Q网络-策略评估网络（double DQN 思想，取小值，缓解高），一个策略提升网络

实际上还有两个目标网络（和Q网络对应，更新方式软更新），使得Q值更稳定，一共五个

Critic--Q网络得损失函数--R经验回放池

这一行好理解

很好理解，把V拆开后，增加了对下个动作的期望

min()里面表示双Q网络求最小值的取值，后一项表示当前状态当前动作的熵

Actor--策略网络的损失函数

本质是最大化：熵+ 动作价值（因为负号变成减法）

最小化：

需要注意的是：

对于连续动作空间的环境，SAC算法的策略输出是高斯分布的均值和标准差，但是高斯分布采样动作的过程是不可导的。

因此，我们需要用到重参数化技巧（reparameterization trick）。

重参数化的做法是先从一个单位高斯分布采样，再把采样值乘以标准差后加上均值。这样就可以认为是从策略高斯分布采样，并且这样对于策略函数是可导的。

函数表示：，其中多余的参数 $\varepsilon _{t}$ 是噪声随机变量，考虑两个Q函数

自动调整熵正则项

熵的系数：在 SAC 算法中，如何选择熵正则项的系数非常重要。在不同的状态下需要不同大小的熵：在最优动作不确定的某个状态下，熵的取值应该大一点；而在某个最优动作比较确定的状态下，熵的取值可以小一点。

所以强化学习的目标：

左边：

在策略 $\pi$ 下，最大化期望累积回报，也即是让智能体在长期运行中获得尽可能多的奖励

右边：约束条件

其中 $\rho _{\pi}$ 是策略 $\pi$ 诱导的状态-动作分布，后面那个是熵。该约束要求策略的熵均值不小于 H ,确保有足够的随机性（探索性），避免陷入局部最优。

所以可以得到权重参数（温度参数）的损失函数---服务于整个SAC。并不局限于哪个网络

通过拉格朗日乘数法将约束优化转化为无约束优化，a是朗格朗日系数（温度参数）

右边第一项：与策略的熵相关，a控制对熵的重视程度。当熵不足时（小于H）,该项促使a调整增加熵

右边第二项：对约束H的惩罚项。通过最小化 L(a) ，动态调整a, 使得策略的熵均值满足H(朗格朗日乘数法的函数，最常见与两个函数图形求交点)，平衡利用（高回报）和探索（熵正则化）。

即当策略的熵低于目标值时，训练目标会使a的值增大，进而在上述最小化损失函数 $L_{\pi}(\theta )$ 的过程中增加了策略熵对应项的重要性；

而当策略的熵高于目标值时，训练目标会使a的值减小，进而使得策略训练时更专注于价值提升

损失函数有两项：1--价值函数，2--策略熵

伪代码

用随机的网络参数 ω1,ω2 和 θ 分别初始化 Critic 网络 Qω1(s,a), Qω2(s,a) 和 Actor 网络 πθ(s)
复制相同的参数 ω1−←ω1, ω2−←ω2，分别初始化目标网络 Qω1− 和 Qω2−
初始化经验回放池 R
for 序列 e=1→E do
- 获取环境初始状态 s1
- for 时间步 t=1→T do
  - 根据当前策略选择动作 at=πθ(st)
  - 执行动作 at，获得奖励 rt，环境状态变为 st+1
  - 将 (st,at,rt,st+1) 存入回放池 R
  - for 训练轮数 k=1→K do
    - 从 R 中采样 N 个元组 {(si,ai,ri,si+1)}i=1,…,N
    - 对每个元组，用目标网络计算
    - 对两个 Critic 网络都进行如下更新：对 j=1,2，最小化损失函数
    - 用重参数化技巧采样动作 a~i，然后用以下损失函数更新当前 Actor 网络：
    - 更新熵正则项的系数 α
    - 更新目标网络
  - end for
- end for
end for

理解一点：Actor-Critic算法其实是就是策略评估和策略提升

Q网络-Critic网络：Q值大不大

策略网络--Actor : 策略好不好

其实就是策略评估和策略提升的循环迭代，高效地在策略空间中搜索最优策略，同时结合价值函数（策略评估）和策略梯度（策略提升）的方法。

代码

import random
import gym
import numpy as np
from tqdm import tqdm
import torch
import torch.nn.functional as F
from torch.distributions import Normal
import matplotlib.pyplot as plt
import rl_utils

定义策略网络和价值网络

连续动作交互环境，策略网络输出一个高斯分布的均值和标准差来表示动作分布

价值网络的输入是状态和动作的拼接向量，输出一个实数来表示动作价值

class PolicyNetContinuous(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
        super(PolicyNetContinuous, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
        self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
        #动作的边界
        self.action_bound = action_bound

    def forward(self, x):
        x = F.relu(self.fc1(x))
        mu = self.fc_mu(x)
        std = F.softplus(self.fc_std(x))
        dist = Normal(mu, std)
        normal_sample = dist.rsample()  # rsample()是重参数化采样
        log_prob = dist.log_prob(normal_sample)
        action = torch.tanh(normal_sample)
        # 计算tanh_normal分布的对数概率密度
        log_prob = log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)
        action = action * self.action_bound

        #将动作缩放到实际的动作边界范围内
        return action, log_prob


class QValueNetContinuous(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNetContinuous, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
        self.fc_out = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x, a):
        #将状态和动作拼接在一起
        cat = torch.cat([x, a], dim=1)
        x = F.relu(self.fc1(cat))
        x = F.relu(self.fc2(x))
        return self.fc_out(x)

分别使用5个网络，一个策略网络，两个价值网络，两个对应的目标价值网络，

使用优化器来更新温度参数

class SACContinuous:
    ''' 处理连续动作的SAC算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, action_bound,
                 actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma,
                 device):
        #五个网络
        self.actor = PolicyNetContinuous(state_dim, hidden_dim, action_dim,
                                         action_bound).to(device)  # 策略网络
        self.critic_1 = QValueNetContinuous(state_dim, hidden_dim,
                                            action_dim).to(device)  # 第一个Q网络
        self.critic_2 = QValueNetContinuous(state_dim, hidden_dim,
                                            action_dim).to(device)  # 第二个Q网络
        self.target_critic_1 = QValueNetContinuous(state_dim,
                                                   hidden_dim, action_dim).to(
                                                       device)  # 第一个目标Q网络
        self.target_critic_2 = QValueNetContinuous(state_dim,
                                                   hidden_dim, action_dim).to(
                                                       device)  # 第二个目标Q网络
        # 令目标Q网络的初始参数和Q网络一样
        self.target_critic_1.load_state_dict(self.critic_1.state_dict())
        self.target_critic_2.load_state_dict(self.critic_2.state_dict())

        #定义优化器--更新模型参数的方法
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
                                                lr=actor_lr)
        self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(),
                                                   lr=critic_lr)
        self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(),
                                                   lr=critic_lr)
        # 使用alpha的log值,可以使训练结果比较稳定
        self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float)
        self.log_alpha.requires_grad = True  # 可以对alpha求梯度
        self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha],
                                                    lr=alpha_lr)

        
        self.target_entropy = target_entropy  # 目标熵的大小
        self.gamma = gamma
        self.tau = tau
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        action = self.actor(state)[0]
        return [action.item()]

    def calc_target(self, rewards, next_states, dones):  # 计算目标Q值
        next_actions, log_prob = self.actor(next_states)
        entropy = -log_prob
        q1_value = self.target_critic_1(next_states, next_actions)
        q2_value = self.target_critic_2(next_states, next_actions)
        next_value = torch.min(q1_value,
                               q2_value) + self.log_alpha.exp() * entropy
        td_target = rewards + self.gamma * next_value * (1 - dones)
        return td_target

    def soft_update(self, net, target_net):
        for param_target, param in zip(target_net.parameters(),
                                       net.parameters()):
            param_target.data.copy_(param_target.data * (1.0 - self.tau) +
                                    param.data * self.tau)

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)
        # 和之前章节一样,对倒立摆环境的奖励进行重塑以便训练
        rewards = (rewards + 8.0) / 8.0

        # 更新两个Q网络
        td_target = self.calc_target(rewards, next_states, dones)
        critic_1_loss = torch.mean(
            F.mse_loss(self.critic_1(states, actions), td_target.detach()))
        critic_2_loss = torch.mean(
            F.mse_loss(self.critic_2(states, actions), td_target.detach()))
        self.critic_1_optimizer.zero_grad()
        critic_1_loss.backward()
        self.critic_1_optimizer.step()
        self.critic_2_optimizer.zero_grad()
        critic_2_loss.backward()
        self.critic_2_optimizer.step()

        # 更新策略网络
        new_actions, log_prob = self.actor(states)
        entropy = -log_prob
        q1_value = self.critic_1(states, new_actions)
        q2_value = self.critic_2(states, new_actions)
        actor_loss = torch.mean(-self.log_alpha.exp() * entropy -
                                torch.min(q1_value, q2_value))
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # 更新alpha值，使用优化器来更新
        alpha_loss = torch.mean(
            (entropy - self.target_entropy).detach() * self.log_alpha.exp())
        self.log_alpha_optimizer.zero_grad()
        alpha_loss.backward()
        self.log_alpha_optimizer.step()

        self.soft_update(self.critic_1, self.target_critic_1)
        self.soft_update(self.critic_2, self.target_critic_2)

倒立摆环境使用SAC算法

env_name = 'Pendulum-v0'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0]  # 动作最大值
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)

actor_lr = 3e-4
critic_lr = 3e-3
alpha_lr = 3e-4
num_episodes = 100
hidden_dim = 128
gamma = 0.99
tau = 0.005  # 软更新参数
buffer_size = 100000
minimal_size = 1000
batch_size = 64
target_entropy = -env.action_space.shape[0]
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
    "cpu")

replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = SACContinuous(state_dim, hidden_dim, action_dim, action_bound,
                      actor_lr, critic_lr, alpha_lr, target_entropy, tau,
                      gamma, device)

return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes,
                                              replay_buffer, minimal_size,
                                              batch_size)

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()

我们要理解的是，SAC原本是为了连续动作的环境提出的，那么SAC是否可以处理离散动作

思考变化：

策略网络的输出修改：在离散动作空间上的softmax分布
价值网络直接接收状态和离散动作空间的分布作为输入

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return F.softmax(self.fc2(x), dim=1)


class QValueNet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(QValueNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

class SAC:
    ''' 处理离散动作的SAC算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
                 alpha_lr, target_entropy, tau, gamma, device):
        # 策略网络
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        # 第一个Q网络
        self.critic_1 = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        # 第二个Q网络
        self.critic_2 = QValueNet(state_dim, hidden_dim, action_dim).to(device)
        self.target_critic_1 = QValueNet(state_dim, hidden_dim,
                                         action_dim).to(device)  # 第一个目标Q网络
        self.target_critic_2 = QValueNet(state_dim, hidden_dim,
                                         action_dim).to(device)  # 第二个目标Q网络
        # 令目标Q网络的初始参数和Q网络一样
        self.target_critic_1.load_state_dict(self.critic_1.state_dict())
        self.target_critic_2.load_state_dict(self.critic_2.state_dict())
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
                                                lr=actor_lr)
        self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(),
                                                   lr=critic_lr)
        self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(),
                                                   lr=critic_lr)
        # 使用alpha的log值,可以使训练结果比较稳定
        self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float)
        self.log_alpha.requires_grad = True  # 可以对alpha求梯度
        self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha],
                                                    lr=alpha_lr)
        self.target_entropy = target_entropy  # 目标熵的大小
        self.gamma = gamma
        self.tau = tau
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.actor(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    # 计算目标Q值,直接用策略网络的输出概率进行期望计算
    def calc_target(self, rewards, next_states, dones):
        next_probs = self.actor(next_states)
        next_log_probs = torch.log(next_probs + 1e-8)
        entropy = -torch.sum(next_probs * next_log_probs, dim=1, keepdim=True)
        q1_value = self.target_critic_1(next_states)
        q2_value = self.target_critic_2(next_states)
        min_qvalue = torch.sum(next_probs * torch.min(q1_value, q2_value),
                               dim=1,
                               keepdim=True)
        next_value = min_qvalue + self.log_alpha.exp() * entropy
        td_target = rewards + self.gamma * next_value * (1 - dones)
        return td_target

    def soft_update(self, net, target_net):
        for param_target, param in zip(target_net.parameters(),
                                       net.parameters()):
            param_target.data.copy_(param_target.data * (1.0 - self.tau) +
                                    param.data * self.tau)

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)  # 动作不再是float类型
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        # 更新两个Q网络
        td_target = self.calc_target(rewards, next_states, dones)
        critic_1_q_values = self.critic_1(states).gather(1, actions)
        critic_1_loss = torch.mean(
            F.mse_loss(critic_1_q_values, td_target.detach()))
        critic_2_q_values = self.critic_2(states).gather(1, actions)
        critic_2_loss = torch.mean(
            F.mse_loss(critic_2_q_values, td_target.detach()))
        self.critic_1_optimizer.zero_grad()
        critic_1_loss.backward()
        self.critic_1_optimizer.step()
        self.critic_2_optimizer.zero_grad()
        critic_2_loss.backward()
        self.critic_2_optimizer.step()

        # 更新策略网络
        probs = self.actor(states)
        log_probs = torch.log(probs + 1e-8)
        # 直接根据概率计算熵
        entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True)  #
        q1_value = self.critic_1(states)
        q2_value = self.critic_2(states)
        min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value),
                               dim=1,
                               keepdim=True)  # 直接根据概率计算期望
        actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue)
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()

        # 更新alpha值
        alpha_loss = torch.mean(
            (entropy - target_entropy).detach() * self.log_alpha.exp())
        self.log_alpha_optimizer.zero_grad()
        alpha_loss.backward()
        self.log_alpha_optimizer.step()

        self.soft_update(self.critic_1, self.target_critic_1)
        self.soft_update(self.critic_2, self.target_critic_2)

actor_lr = 1e-3
critic_lr = 1e-2
alpha_lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
tau = 0.005  # 软更新参数
buffer_size = 10000
minimal_size = 500
batch_size = 64
target_entropy = -1
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
    "cpu")

env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = SAC(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, alpha_lr,
            target_entropy, tau, gamma, device)

return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes,
                                              replay_buffer, minimal_size,
                                              batch_size)

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()

可以发现，在离散环境下，SAC具有完美的收敛性能，并且其策略回报的曲线十分稳定。

区别

离散环境和连续环境

对比项	离散动作版本	连续动作版本
策略网络输出	动作概率分布（Categorical）	动作均值和标准差（Normal 分布）
Q 网络输入	仅状态（输出所有动作的 Q 值）	状态 + 动作（输出单个 Q 值）
动作选择	直接采样概率分布（`Categorical.sample()`）	重参数化采样（`Normal.rsample()`）
Q 值期望计算	概率加权求和（`torch.sum(probs * q_values)`）	采样动作后计算（`Q(s, a)`）
熵计算	直接基于概率分布（`-sum(p * log p)`）	基于采样动作的对数概率（`log_prob`）

TD3

介绍

Twin Delayed Deep Deterministic policy gradient(几个关键字：双延迟，深度，确定性策略，梯度)

在DDPG的基础上改进的用于解决连续控制问题的在线（on -line）异策（off-policy）的深度强化学习算法。本质上，TD3算法就是将DQN算法的思想融入到DDPG中。

所以说TD3一共6个网络

1. Actor网络（策略网络）

在线Actor网络（Online Actor）：实时与环境交互，生成动作策略。
目标Actor网络（Target Actor）：用于计算目标Q值的动作生成，参数通过软更新（Polyak平均）从在线Actor同步。

2. Critic网络（价值评估网络）

双在线Critic网络（Critic1 & Critic2）：两个独立网络分别评估Q值，取较小值避免过估计。
双目标Critic网络（Target Critic1 & Target Critic2）：对应在线Critic的延迟版本，用于计算目标Q值。

总计：2（Actor） + 4（Critic） = 6个网络。

核心差异:

维度	DDPG	TD3
Q 网络数量	主网络 1 个，目标网络 1 个	主网络 2 个，目标网络 2 个
目标 Q 计算	单一 Q 网络估计值	双 Q 网络最小值
策略更新频率	与 Q 网络同步更新	延迟更新（例如每两步一次）
探索机制	依赖 OU 噪声或高斯噪声	目标策略平滑（噪声 + 剪辑）
过估计控制	弱（依赖目标网络延迟）	强（双 Q 网络 + 策略平滑）

三个关键技术

双重网络：两套Critic网络，计算时取最小值，抑制网络过估计问题，实验证明：两套就够了，再多的也没有用。
目标策略平滑正则化：计算目标值时，在下一个状态的动作上加入扰动，从而使得价值评估更加准确。因为如果某个动作偶然获得高奖励，Q网络可能将其附近的状态价值估计推向极端
延迟更新：Critic网络更新多次后，在更新Actor网络，从而保证Actor网络的训练更加稳定（Q网络估计不准确导致的策略震荡，提升训练稳定性，也就是说Critic网络不稳定，那么Actor网络也不会稳定。）

目标策略正则化处理-针对Q网络（Critic网络）

正则化：简单来说，就是在模型的损失函数中额外增添一个附加项，借助这个附加项对模型参数的数值进行约束，避免模型过度关注训练数据里的噪声或者细节。

理论上来说，应该利用目标动作周围的区域来计算目标，从而有利于平滑估计值。

在实际操作中，通过向目标动作中添加少量随噪声，并在小批量中求平均值，来近似动作的期望。

注意：添加的噪声是服从正态分布的，并且对采样的噪声做了裁剪，以保持目标接近原始动作。

更新过程-伪代码

和DDPG相差不大，主要区别在于目标值的计算方式

Actor网络通过最大化累积期望回报来更新
Critic1和Critic2网络通过最小化评估值和目标值之间的误差来更新
所有目标网络都采用软更新的方式来更新

具体而言

Critic1和 Critic 2 网络：

利用Target Actor 网络计算出状态下的动作
然后基于目标策略平滑正则化，在目标动作上加入噪声
接着基于双重网络的思想，计算目标值
最后利用梯度下降法最小化评估值和目标值之间的误差，从而对Critic 1 和 Critic 2网络中的参数进行更新

Actor 网络：

在Critic 1 和 Critic 2网络更新 d 步之后，启动Actor网络更新，利用Actor网络计算状态下的动作-------注意：这里计算出的动作不需要加入噪声，因为这里希望Actor网络能够朝着最大值方向更新，加入噪声没有任何意义
然后利用Critic 1 和 Critic 2网络计算状态动作对的评估值
最后梯度上升最大化Q

目标网络的更新过程：

采用软更新方式对目标网络进行更新
引入学习率，将旧的目标网络参数和新的网络参数做加权平均，然后赋值给目标网络，学习率通常取值0.005

伪代码：

初始化:
    初始化策略网络 π(s; θ_π) 和目标策略网络 π'(s; θ_π')，且 θ_π' ← θ_π
    初始化两个 Q 网络 Q1(s, a; θ_Q1) 和 Q2(s, a; θ_Q2)，以及对应的目标 Q 网络 Q1'(s, a; θ_Q1') 和 Q2'(s, a; θ_Q2')，且 θ_Q1' ← θ_Q1，θ_Q2' ← θ_Q2
    初始化经验回放缓冲区 R
    初始化超参数:
        折扣因子 γ
        软更新系数 τ
        策略更新延迟频率 d
        噪声标准差 σ
        噪声截断值 c
        批量大小 N
        学习率 α_π（策略网络），α_Q（Q 网络）

for 每个回合 do
    初始化环境状态 s
    for 回合中的每个时间步 t do
        从策略网络 π 中选择动作 a = π(s; θ_π)，并添加噪声：
            a = a + clip(ϵ, -c, c)，其中 ϵ ~ N(0, σ²)
        执行动作 a，观察奖励 r 和下一个状态 s'
        将转移 (s, a, r, s', done) 存储到经验回放缓冲区 R 中
        s ← s'
        
        从经验回放缓冲区 R 中随机采样一个批量大小为 N 的转移集合 B = {(s, a, r, s', done)}
        for 转移 (s, a, r, s', done) in B do
            计算目标动作 a'：
                a' = π'(s'; θ_π') + clip(ϵ', -c, c)，其中 ϵ' ~ N(0, σ²)
            计算目标 Q 值：
                y = r + γ * (1 - done) * min(Q1'(s', a'; θ_Q1'), Q2'(s', a'; θ_Q2'))
            更新 Q 网络：
                计算 Q1 的损失 L_Q1 = MSE(Q1(s, a; θ_Q1), y)
                计算 Q2 的损失 L_Q2 = MSE(Q2(s, a; θ_Q2), y)
                计算总的 Q 网络损失 L_Q = L_Q1 + L_Q2
                通过梯度下降更新 θ_Q1 和 θ_Q2：
                    θ_Q1 ← θ_Q1 - α_Q * ∇θ_Q1 L_Q
                    θ_Q2 ← θ_Q2 - α_Q * ∇θ_Q2 L_Q
        
        如果 t % d == 0 then
            更新策略网络：
                计算策略网络损失 L_π = -mean(Q1(s, π(s; θ_π); θ_Q1))
                通过梯度下降更新 θ_π：
                    θ_π ← θ_π - α_π * ∇θ_π L_π
            软更新目标网络：
                θ_π' ← τ * θ_π + (1 - τ) * θ_π'
                θ_Q1' ← τ * θ_Q1 + (1 - τ) * θ_Q1'
                θ_Q2' ← τ * θ_Q2 + (1 - τ) * θ_Q2'
    end for
end for

代码

Replay Buffer 实现

import numpy as np
 
 
class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim, batch_size):
        self.mem_size = max_size
        self.batch_size = batch_size
        self.mem_cnt = 0
 
        self.state_memory = np.zeros((max_size, state_dim))
        self.action_memory = np.zeros((max_size, action_dim))
        self.reward_memory = np.zeros((max_size, ))
        self.next_state_memory = np.zeros((max_size, state_dim))
        self.terminal_memory = np.zeros((max_size, ), dtype=np.bool)
 
    def store_transition(self, state, action, reward, state_, done):
        #存储状态
        mem_idx = self.mem_cnt % self.mem_size
 
        self.state_memory[mem_idx] = state
        self.action_memory[mem_idx] = action
        self.reward_memory[mem_idx] = reward
        self.next_state_memory[mem_idx] = state_
        self.terminal_memory[mem_idx] = done
 
        self.mem_cnt += 1
 
    def sample_buffer(self):
        #采样
        mem_len = min(self.mem_cnt, self.mem_size)
        batch = np.random.choice(mem_len, self.batch_size, replace=False)
 
        states = self.state_memory[batch]
        actions = self.action_memory[batch]
        rewards = self.reward_memory[batch]
        states_ = self.next_state_memory[batch]
        terminals = self.terminal_memory[batch]
 
        return states, actions, rewards, states_, terminals
 
    def ready(self):
        #检查是否准备就绪
        return self.mem_cnt >= self.batch_size

Actor 和 Critic 网络的实现

import torch as T
import torch.nn as nn
import torch.optim as optim
 
device = T.device("cuda:0" if T.cuda.is_available() else "cpu")
 
 
class ActorNetwork(nn.Module):
    def __init__(self, alpha, state_dim, action_dim, fc1_dim, fc2_dim):
        super(ActorNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, fc1_dim)
        self.ln1 = nn.LayerNorm(fc1_dim)
        self.fc2 = nn.Linear(fc1_dim, fc2_dim)
        self.ln2 = nn.LayerNorm(fc2_dim)
        self.action = nn.Linear(fc2_dim, action_dim)
 
        self.optimizer = optim.Adam(self.parameters(), lr=alpha)
        self.to(device)
 
    def forward(self, state):
        x = T.relu(self.ln1(self.fc1(state)))
        x = T.relu(self.ln2(self.fc2(x)))
        action = T.tanh(self.action(x))
 
        return action
 
    def save_checkpoint(self, checkpoint_file):
        #保存模型方法--保存到指定文件
        T.save(self.state_dict(), checkpoint_file, _use_new_zipfile_serialization=False)
 
    def load_checkpoint(self, checkpoint_file):
        #加载模型方法--从指定文件加载网络参数
        self.load_state_dict(T.load(checkpoint_file))
 
 
class CriticNetwork(nn.Module):
    def __init__(self, beta, state_dim, action_dim, fc1_dim, fc2_dim):
        super(CriticNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim+action_dim, fc1_dim)
        self.ln1 = nn.LayerNorm(fc1_dim)
        self.fc2 = nn.Linear(fc1_dim, fc2_dim)
        self.ln2 = nn.LayerNorm(fc2_dim)
        self.q = nn.Linear(fc2_dim, 1)
 
        self.optimizer = optim.Adam(self.parameters(), lr=beta)
        self.to(device)
 
    def forward(self, state, action):
        x = T.cat([state, action], dim=-1)
        x = T.relu(self.ln1(self.fc1(x)))
        x = T.relu(self.ln2(self.fc2(x)))
        q = self.q(x)
 
        return q
 
    def save_checkpoint(self, checkpoint_file):
        T.save(self.state_dict(), checkpoint_file, _use_new_zipfile_serialization=False)
 
    def load_checkpoint(self, checkpoint_file):
        self.load_state_dict(T.load(checkpoint_file))

实现TD3算法

import torch as T
import torch.nn.functional as F
import numpy as np
from networks import ActorNetwork, CriticNetwork
from buffer import ReplayBuffer
 
device = T.device("cuda:0" if T.cuda.is_available() else "cpu")
 
 
class TD3:
    def __init__(self, alpha, beta, state_dim, action_dim, actor_fc1_dim, actor_fc2_dim,
                 critic_fc1_dim, critic_fc2_dim, ckpt_dir, gamma=0.99, tau=0.005, action_noise=0.1,
                 policy_noise=0.2, policy_noise_clip=0.5, delay_time=2, max_size=1000000,
                 batch_size=256):
        self.gamma = gamma
        self.tau = tau
        self.action_noise = action_noise
        self.policy_noise = policy_noise
        self.policy_noise_clip = policy_noise_clip
        self.delay_time = delay_time
        self.update_time = 0
        self.checkpoint_dir = ckpt_dir
 
        self.actor = ActorNetwork(alpha=alpha, state_dim=state_dim, action_dim=action_dim,
                                  fc1_dim=actor_fc1_dim, fc2_dim=actor_fc2_dim)
        self.critic1 = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
                                     fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
        self.critic2 = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
                                     fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
 
        self.target_actor = ActorNetwork(alpha=alpha, state_dim=state_dim, action_dim=action_dim,
                                         fc1_dim=actor_fc1_dim, fc2_dim=actor_fc2_dim)
        self.target_critic1 = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
                                            fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
        self.target_critic2 = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
                                            fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
 
        self.memory = ReplayBuffer(max_size=max_size, state_dim=state_dim, action_dim=action_dim,
                                   batch_size=batch_size)
 
        self.update_network_parameters(tau=1.0)
 
    def update_network_parameters(self, tau=None):
        #软更新
        if tau is None:
            tau = self.tau
 
        for actor_params, target_actor_params in zip(self.actor.parameters(),
                                                     self.target_actor.parameters()):
            target_actor_params.data.copy_(tau * actor_params + (1 - tau) * target_actor_params)
 
        for critic1_params, target_critic1_params in zip(self.critic1.parameters(),
                                                         self.target_critic1.parameters()):
            target_critic1_params.data.copy_(tau * critic1_params + (1 - tau) * target_critic1_params)
 
        for critic2_params, target_critic2_params in zip(self.critic2.parameters(),
                                                         self.target_critic2.parameters()):
            target_critic2_params.data.copy_(tau * critic2_params + (1 - tau) * target_critic2_params)
 
    def remember(self, state, action, reward, state_, done):
        #经验存储方法
        self.memory.store_transition(state, action, reward, state_, done)
 
    def choose_action(self, observation, train=True):
        #动作选择方法
        self.actor.eval()
        state = T.tensor([observation], dtype=T.float).to(device)
        action = self.actor.forward(state)
 
        if train:
            # exploration noise
            noise = T.tensor(np.random.normal(loc=0.0, scale=self.action_noise),
                             dtype=T.float).to(device)
            action = T.clamp(action+noise, -1, 1)
        self.actor.train()
 
        return action.squeeze().detach().cpu().numpy()
 
    def learn(self):
        if not self.memory.ready():
            return
 
        states, actions, rewards, states_, terminals = self.memory.sample_buffer()
        states_tensor = T.tensor(states, dtype=T.float).to(device)
        actions_tensor = T.tensor(actions, dtype=T.float).to(device)
        rewards_tensor = T.tensor(rewards, dtype=T.float).to(device)
        next_states_tensor = T.tensor(states_, dtype=T.float).to(device)
        terminals_tensor = T.tensor(terminals).to(device)
 
        with T.no_grad():
            next_actions_tensor = self.target_actor.forward(next_states_tensor)
            action_noise = T.tensor(np.random.normal(loc=0.0, scale=self.policy_noise),
                                    dtype=T.float).to(device)
            # smooth noise
            action_noise = T.clamp(action_noise, -self.policy_noise_clip, self.policy_noise_clip)
            next_actions_tensor = T.clamp(next_actions_tensor+action_noise, -1, 1)
            q1_ = self.target_critic1.forward(next_states_tensor, next_actions_tensor).view(-1)
            q2_ = self.target_critic2.forward(next_states_tensor, next_actions_tensor).view(-1)
            q1_[terminals_tensor] = 0.0
            q2_[terminals_tensor] = 0.0
            critic_val = T.min(q1_, q2_)
            target = rewards_tensor + self.gamma * critic_val
        q1 = self.critic1.forward(states_tensor, actions_tensor).view(-1)
        q2 = self.critic2.forward(states_tensor, actions_tensor).view(-1)
 
        critic1_loss = F.mse_loss(q1, target.detach())
        critic2_loss = F.mse_loss(q2, target.detach())
        critic_loss = critic1_loss + critic2_loss
        self.critic1.optimizer.zero_grad()
        self.critic2.optimizer.zero_grad()
        critic_loss.backward()
        self.critic1.optimizer.step()
        self.critic2.optimizer.step()
 
        self.update_time += 1
        if self.update_time % self.delay_time != 0:
            return
 
        new_actions_tensor = self.actor.forward(states_tensor)
        q1 = self.critic1.forward(states_tensor, new_actions_tensor)
        actor_loss = -T.mean(q1)
        self.actor.optimizer.zero_grad()
        actor_loss.backward()
        self.actor.optimizer.step()
 
        self.update_network_parameters()
 
    def save_models(self, episode):
        self.actor.save_checkpoint(self.checkpoint_dir + 'Actor/TD3_actor_{}.pth'.format(episode))
        print('Saving actor network successfully!')
        self.target_actor.save_checkpoint(self.checkpoint_dir +
                                          'Target_actor/TD3_target_actor_{}.pth'.format(episode))
        print('Saving target_actor network successfully!')
        self.critic1.save_checkpoint(self.checkpoint_dir + 'Critic1/TD3_critic1_{}.pth'.format(episode))
        print('Saving critic1 network successfully!')
        self.target_critic1.save_checkpoint(self.checkpoint_dir +
                                            'Target_critic1/TD3_target_critic1_{}.pth'.format(episode))
        print('Saving target critic1 network successfully!')
        self.critic2.save_checkpoint(self.checkpoint_dir + 'Critic2/TD3_critic2_{}.pth'.format(episode))
        print('Saving critic2 network successfully!')
        self.target_critic2.save_checkpoint(self.checkpoint_dir +
                                            'Target_critic2/TD3_target_critic2_{}.pth'.format(episode))
        print('Saving target critic2 network successfully!')
 
    def load_models(self, episode):
        self.actor.load_checkpoint(self.checkpoint_dir + 'Actor/TD3_actor_{}.pth'.format(episode))
        print('Loading actor network successfully!')
        self.target_actor.load_checkpoint(self.checkpoint_dir +
                                          'Target_actor/TD3_target_actor_{}.pth'.format(episode))
        print('Loading target_actor network successfully!')
        self.critic1.load_checkpoint(self.checkpoint_dir + 'Critic1/TD3_critic1_{}.pth'.format(episode))
        print('Loading critic1 network successfully!')
        self.target_critic1.load_checkpoint(self.checkpoint_dir +
                                            'Target_critic1/TD3_target_critic1_{}.pth'.format(episode))
        print('Loading target critic1 network successfully!')
        self.critic2.load_checkpoint(self.checkpoint_dir + 'Critic2/TD3_critic2_{}.pth'.format(episode))
        print('Loading critic2 network successfully!')
        self.target_critic2.load_checkpoint(self.checkpoint_dir +
                                            'Target_critic2/TD3_target_critic2_{}.pth'.format(episode))
        print('Loading target critic2 network successfully!')

训练脚本

import gym
import numpy as np
import argparse
from TD3 import TD3
from utils import create_directory, plot_learning_curve, scale_action
 
parser = argparse.ArgumentParser()
parser.add_argument('--max_episodes', type=int, default=1000)
parser.add_argument('--ckpt_dir', type=str, default='./checkpoints/TD3/')
parser.add_argument('--figure_file', type=str, default='./output_images/reward.png')
 
args = parser.parse_args()
 
 
def main():
    env = gym.make('LunarLanderContinuous-v2')
    agent = TD3(alpha=0.0003, beta=0.0003, state_dim=env.observation_space.shape[0],
                action_dim=env.action_space.shape[0], actor_fc1_dim=400, actor_fc2_dim=300,
                critic_fc1_dim=400, critic_fc2_dim=300, ckpt_dir=args.ckpt_dir, gamma=0.99,
                tau=0.005, action_noise=0.1, policy_noise=0.2, policy_noise_clip=0.5,
                delay_time=2, max_size=1000000, batch_size=256)
    create_directory(path=args.ckpt_dir, sub_path_list=['Actor', 'Critic1', 'Critic2', 'Target_actor',
                                                        'Target_critic1', 'Target_critic2'])
 
    total_reward_history = []
    avg_reward_history = []
    for episode in range(args.max_episodes):
        total_reward = 0
        done = False
        observation = env.reset()
        while not done:
            action = agent.choose_action(observation, train=True)
            action_ = scale_action(action, low=env.action_space.low, high=env.action_space.high)
            observation_, reward, done, info = env.step(action_)
            agent.remember(observation, action, reward, observation_, done)
            agent.learn()
            total_reward += reward
            observation = observation_
        total_reward_history.append(total_reward)
        avg_reward = np.mean(total_reward_history[-100:])
        avg_reward_history.append(avg_reward)
        print('Ep: {} Reward: {} AvgReward: {}'.format(episode+1, total_reward, avg_reward))
 
        if (episode + 1) % 200 == 0:
            agent.save_models(episode+1)
 
    episodes = [i+1 for i in range(args.max_episodes)]
    plot_learning_curve(episodes, avg_reward_history, title='AvgReward', ylabel='reward',
                        figure_file=args.figure_file)
 
 
if __name__ == '__main__':
    main()

训练脚本中有三个参数，max_episodes表示训练幕数，checkpoint_dir表示训练权重保存路径，figure_file表示训练结果的保存路径（其实是一张累积奖励曲线图），按照默认设置即可。

提供utils.py脚本

import os
import numpy as np
import matplotlib.pyplot as plt
 
 
def create_directory(path: str, sub_path_list: list):
    for sub_path in sub_path_list:
        if not os.path.exists(path + sub_path):
            os.makedirs(path + sub_path, exist_ok=True)
            print('Path: {} create successfully!'.format(path + sub_path))
        else:
            print('Path: {} is already existence!'.format(path + sub_path))
 
 
def plot_learning_curve(episodes, records, title, ylabel, figure_file):
    plt.figure()
    plt.plot(episodes, records, color='b', linestyle='-')
    plt.title(title)
    plt.xlabel('episode')
    plt.ylabel(ylabel)
 
    plt.show()
    plt.savefig(figure_file)
 
 
def scale_action(action, low, high):
    action = np.clip(action, -1, 1)
    weight = (high - low) / 2
    bias = (high + low) / 2
    action_ = action * weight + bias
 
    return action_

提供测试代码，用于测试训练效果和观察环境的动态渲染

import gym
import imageio
import argparse
from TD3 import TD3
from utils import scale_action
 
parser = argparse.ArgumentParser()
parser.add_argument('--ckpt_dir', type=str, default='./checkpoints/TD3/')
parser.add_argument('--figure_file', type=str, default='./output_images/LunarLander.gif')
parser.add_argument('--fps', type=int, default=30)
parser.add_argument('--render', type=bool, default=True)
parser.add_argument('--save_video', type=bool, default=True)
 
args = parser.parse_args()
 
 
def main():
    env = gym.make('LunarLanderContinuous-v2')
    agent = TD3(alpha=0.0003, beta=0.0003, state_dim=env.observation_space.shape[0],
                action_dim=env.action_space.shape[0], actor_fc1_dim=400, actor_fc2_dim=300,
                critic_fc1_dim=400, critic_fc2_dim=300, ckpt_dir=args.ckpt_dir, gamma=0.99,
                tau=0.005, action_noise=0.1, policy_noise=0.2, policy_noise_clip=0.5,
                delay_time=2, max_size=1000000, batch_size=256)
    agent.load_models(1000)
    video = imageio.get_writer(args.figure_file, fps=args.fps)
 
    done = False
    observation = env.reset()
    while not done:
        if args.render:
            env.render()
        action = agent.choose_action(observation, train=True)
        action_ = scale_action(action, low=env.action_space.low, high=env.action_space.high)
        observation_, reward, done, info = env.step(action_)
        observation = observation_
        if args.save_video:
            video.append_data(env.render(mode='rgb_array'))
 
 
if __name__ == '__main__':
    main()

测试脚本中包括五个参数，filename表示环境动态图的保存路径，checkpoint_dir表示加载的权重路径，save_video表示是否要保存动态图，fps表示动态图的帧率，rander表示是否开启环境渲染。大家只需要调整save_video和rander这两个参数，其余保持默认即可

总结

将这些算法进行一个总结

一、基于 Actor-Critic框架的算法

算法	网络数量	核心设计思想
SAC	5	最大化熵+双Critic保守估计
DDPG	4	确定性策略+目标网络稳定训练
TD3	6	双Critic+延迟更新+目标策略平滑
TRPO/PPO	2	约束策略更新幅度（TRPO）或目标函数（PPO）

1.SAC(soft actor-critic)

网络数量：5（Actor + 2 在线critic + 2 目标 Critic）
- Actor:输出含熵的随即策略，平衡探索和利用
- 在线critic1和critic2：独立评估Q值，取最小值避免过估计，但是还会波动
- 目标 crictic1 和 critic 2 ：通过软更新，稳定Q值计算按，不波动了
- 温度参数：自动调节熵权重（非网络，可以学习参数）

2.DDPG（Deep Deterministic Policy Gradient）

网络数量：4（在线Actor + 目标Actor + 在线 Critic +目标 Critic）
- 在线Actor : 生成确定性动作
- 目标Actor : 软更新策略，减少策略震荡
- 在线Critic : 评估动作Q值
- 目标 Critic：计算目标Q值（软更新）

3.TD3(Twin Delayed DDPG)

网络数量：6（在线Actor + 目标Actor + 2在线 Critic +2目标 Critic）
- 双在线Critic : 独立评估Q值，取最小值保守估计
- 双目标Critic : 延迟更新，与目标Actor配合计算目标Q值
- 目标Actor：生成平滑动作，添加噪声防止过拟合

4.TRPO/PPO（策略优化类，在AC框架上专攻策略更新的稳定性与效率，优化Critic网络）

网络数量：2 （策略网络 + 价值网络）
- 策略网络：输出动作分布，TRPO通过KL散度约束更新幅度，PPO通过剪切目标函数限制更新
- 价值网络：评估状态价值函数，辅助策略梯度更新

思考一下：为什么SAC,DDPG等算法的Critic网络不引入TRPO/PPO算法的思想？

SAC等相当于预测模型，而TRPO相当于控制器设计，前者追求预测准确，后者追求控制稳定
TRPO计算复杂度高，引入之后可能得不偿失
在SAC等中，Critic仅提供Q值梯度，Actor独立更新策略，TRPO的约束需要同时作用在策略和值函数，显然这样会不行
DDPG的软更新本质上就是延迟约束，过多约束并不太好

二、经典Actor-Critic与DQN系列

1.基础Actor-Critic

网络数量：2 （Actor + Critic）
- Actor：策略网络，输出动作概率分布
- Critic：价值网络，评估状态或动作价值，提供策略梯度方向

2.DQN (Deep Q-learning)

网络数量：2 （在线网络+目标网络）
- 在线网络：预测当前Q值，选择动作，进行采样
- 目标网络：软更新，经验放回池计算目标Q值： $y = =r + \gamma maxQ_{target}(s')$ ，这个公式就有两个意思，找到使Q最大的动作，计算Q值

3.Double DQN

网络数量：2 （结构同DQN）
- 改进点：用在线网络选择动作，目标网络评估Q值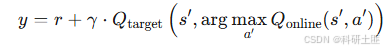，目标网络计算值（在经验放回池中进行在线网络和目标网络都在经验放回池中行进行，在线网络还需要和环境交互），解决DQN的Q值过估计问题

4.Dueling DQN

网络数量：2 （在线网络 + 目标网络）
- 结构特性：Q网络差分为价值流和优势流，组合 $Q = V +A$
- 优势：分离状态价值和动作优势，组成生成在线网络，目标网络也是这样的双流结构，提升稀疏奖励下的学习效率，更加关心动作的差异性
- Dueling DQN并未增加网络数量，而是重构了单网络的内部架构，双流计算共享部分底层特征（例如：卷积层），仅仅在高层分离为V和A分支。

算法	网络数量	核心设计思想
Actor-Critic	2	策略与价值评估解耦
DQN系列	2	目标网络稳定训练，结构改进降低估计偏差

关键点解析

目标网络的意义：通过延迟更新（如DDPG、TD3）或周期性复制（如DQN），减少自举法（Bootstrapping）带来的Q值震荡。
双Critic设计：TD3和SAC通过双Critic取最小/平均Q值，约束过估计问题。
策略优化核心：
- DDPG/TD3：确定性策略（适合连续动作空间）。
- SAC：随机策略+熵最大化（平衡探索与利用）。
- TRPO/PPO：基于重要性采样的策略梯度（适合高维离散动作）