数据结构：队列

目录

队列的概念和结构

队列的实现

结构定义

初始化

判空

入队列

出队列

返回队头元素

返回队尾元素

返回size

销毁 

---

队列的概念和结构

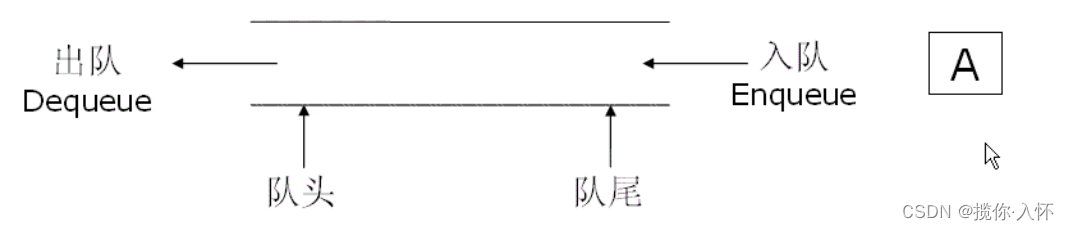
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头

队列的实现

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，牵扯挪动数据覆盖，效率会比较低。

结构定义

typedef int QueueDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QueueDataType data;
}QNode;

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;

初始化

void QueueInit(Queue* pq)
{
	assert(pq);

	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}

判空

删除元素和返回队列元素需要判空。

bool QueueEmpty(Queue* pq)
{
	assert(pq);

	return pq->phead == NULL && pq->ptail == NULL;
}

入队列

void QueuePush(Queue* pq, QueueDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("maoolc fail");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;
	//无节点
	if (pq->phead == NULL)
	{
		assert(pq->ptail == NULL);
		pq->phead = pq->ptail = newnode;
	}
	//多个节点
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

出队列

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	//一个节点
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else
	{
		QNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}

	pq->size--;
}

返回队头元素

QueueDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}

返回队尾元素

QueueDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

返回size

int Queuesize(Queue* pq)
{
	assert(pq);

	return pq->size;
}

销毁 

void QueueDestroy(Queue* pq)
{
	assert(pq);

	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

队列oj

1.用队列实现栈

oj链接

 这道题目利用两个队列实现栈，栈的特点是先进后出。所以出栈就用两个队列来回倒数据。倒到最后一个数据就是要出栈的数据。至于入栈就交给有数据的队列即可。

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() {
    MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
    if(NULL == obj)
    {
        perror("malloc fail");
        return NULL;
    }
    QueueInit(&obj->q1);
    QueueInit(&obj->q2);

    return obj;
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

int myStackPop(MyStack* obj) {
    Queue* qEmptyp = &obj->q1;
    Queue* qNonEmptyp = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
         qEmptyp = &obj->q2;
        qNonEmptyp = &obj->q1;
    }

    //倒数据
    while(Queuesize(qNonEmptyp)>1)
    {
        QueuePush(qEmptyp,QueueFront(qNonEmptyp));
        QueuePop(qNonEmptyp);
    }

    int top = QueueFront(qNonEmptyp);
    QueuePop(qNonEmptyp);

    return top;
}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

2.用栈实现队列

 oj链接

图解：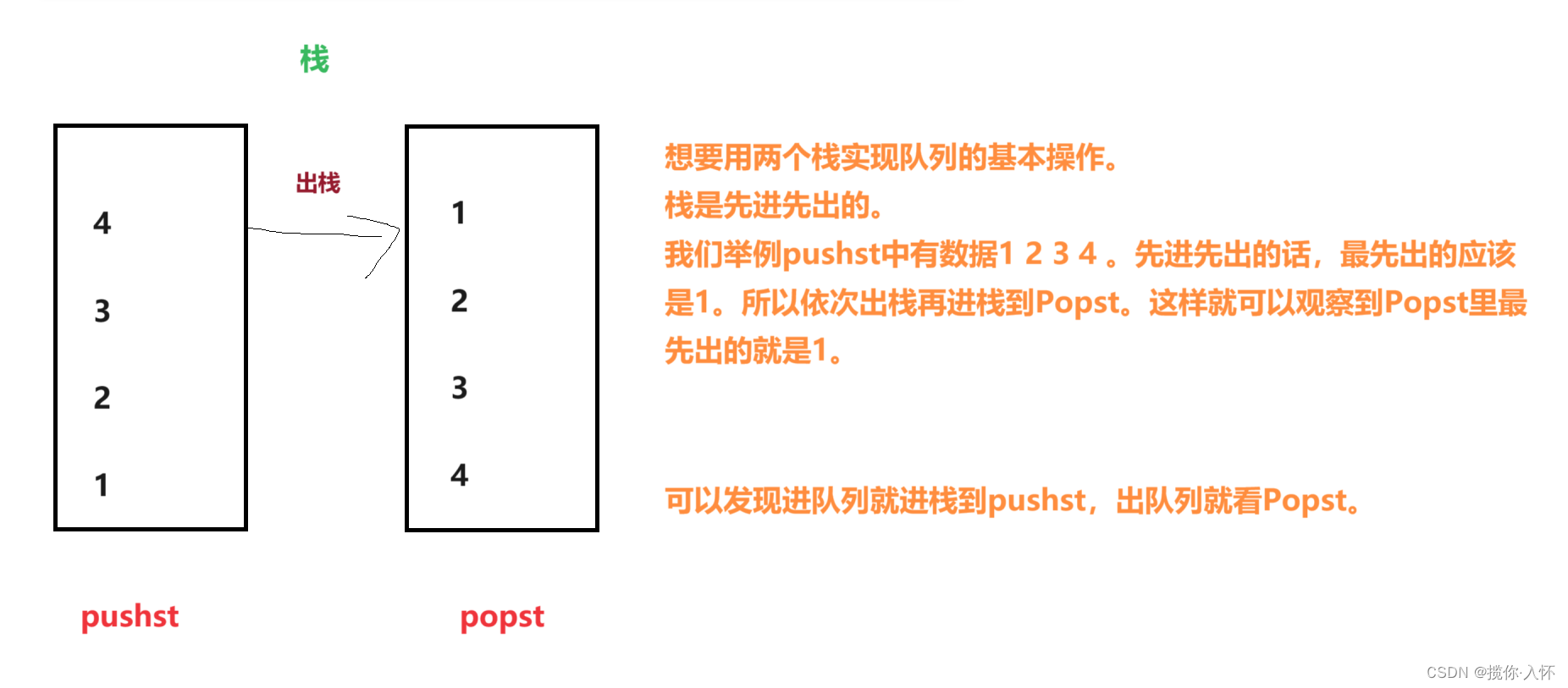

typedef struct {
    ST pushst;
    ST popst;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
    if(NULL == obj)
    {
        perror("malloc fail");
    }

    STInit(&obj->pushst);
    STInit(&obj->popst);

    return obj; 
}

void myQueuePush(MyQueue* obj, int x) {
    STPush(&obj->pushst,x);
}

int myQueuePeek(MyQueue* obj) {
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->popst,STTop(&obj->pushst));
            STPop(&obj->pushst);       
        }
    }

    return STTop(&obj->popst);
}

int myQueuePop(MyQueue* obj) {
    int top = myQueuePeek(obj);
    STPop(&obj->popst);
    return top;
}



bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->pushst) &&
   STEmpty(&obj->popst);
}

void myQueueFree(MyQueue* obj) {
    STDestroy(&obj->popst);
    STDestroy(&obj->pushst);

    free(obj);
}

 3.设计循环队列

oj链接

可以用数组实现循环队列，也可以使用链表。我是用的是数组。因为题目需要返回队尾数据，数组方便一些。

typedef struct {
    int k;
    int front;//头
    int rear;//尾
    int* a;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int)*(k+1));
    obj->front = obj->rear = 0;
    obj->k = k;
    return obj;                                                                                                   
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear+1)%(obj->k+1) == obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    else
    {
        obj->a[obj->rear] = value;
        obj->rear++;
        obj->rear %= (obj->k+1);

        return true;
    }

}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    else
    {
        obj->front++;
        obj->front %= (obj->k+1);

        return true;
    }
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    {
        return obj->a[obj->front];
    }
}

int myCircularQueueRear(MyCircularQueue* obj) {
     if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    {
        return obj->a[(obj->rear+obj->k)%(obj->k+1)];
    }
}


void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

总结

队列作为一种常见的数据结构，在计算机科学中有广泛的应用，通常运用于广度优先搜索、任务调度等场景。希望这篇文章可以帮助到你更好的学习和理解队列的知识。