文章目录
- 矩阵
-
- Solution73. 矩阵置零
- Solution54. 螺旋矩阵
- Solution48. 旋转图像
- Solution240. 搜索二维矩阵 II
- 二叉树
-
- 二叉树的四种遍历结果
- Solution94. 二叉树的中序遍历
- Solution104. 二叉树的最大深度
- Solution226. 翻转二叉树
- Solution101. 对称二叉树
- Solution543. 二叉树的直径
- Solution102. 二叉树的层序遍历
- Solution108. 将有序数组转换为二叉搜索树
- Solution98. 验证二叉搜索树
- Solution230. 二叉搜索树中第 K 小的元素
- Solution199. 二叉树的右视图
- Solution114. 二叉树展开为链表
- Solution105. 从前序与中序遍历序列构造二叉树
- Solution437. 路径总和 III
- Solution236. 二叉树的最近公共祖先
矩阵
Solution73. 矩阵置零
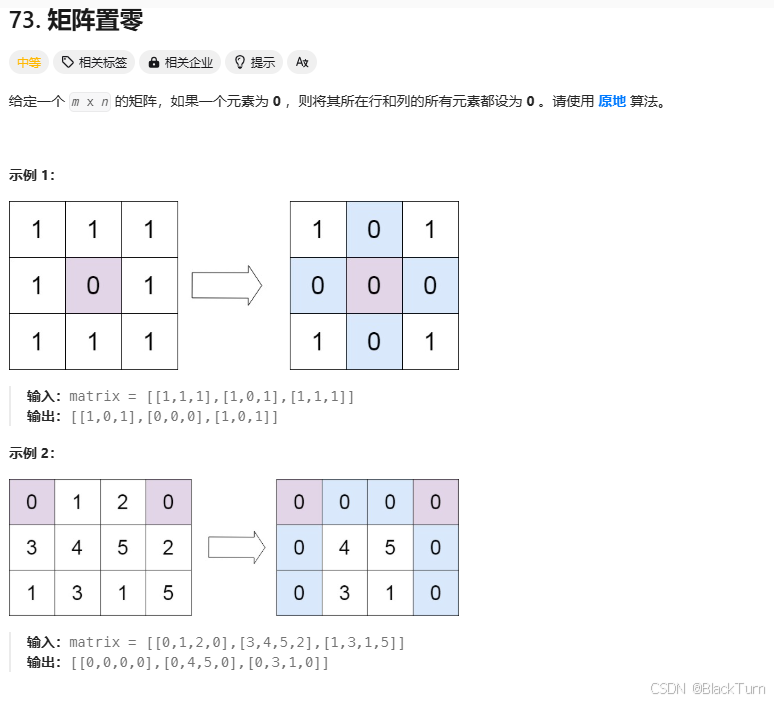
代码思路说明:
假如矩阵是
{1, 2, 3},
{4, 0, 6},
{7, 8, 9}
第一次遍历矩阵,得到两个数组:
zeroRows = [false, true, false],这个zeroRows记录需要置零的行,第二行需要置零
zeroCols = [false, true, false],这个zeroCols记录需要置零的列,第二列需要置零
第二次遍历矩阵,
如果某个元素所在的行或列被标记为需要置零,则将该元素置为零;如元素4所在的行被标记为需要置零,则将该元素置为零
public class Solution {
public static void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
boolean[] zeroRows = new boolean[m];
boolean[] zeroCols = new boolean[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
zeroRows[i] = true;
zeroCols[j] = true;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (zeroRows[i] || zeroCols[j]) {
matrix[i][j] = 0;
}
}
}
}
public static void main(String[] args) {
int[][] matrix = {
{
1, 2, 3},
{
4, 0, 6},
{
7, 8, 9}
};
System.out.println("原始矩阵:");
printMatrix(matrix);
setZeroes(matrix);
System.out.println("处理后的矩阵:");
printMatrix(matrix);
}
public static void printMatrix(int[][] matrix) {
for (int[] row : matrix) {
for (int num : row) {
System.out.print(num + " ");
}
System.out.println();
}
}
}
Solution54. 螺旋矩阵
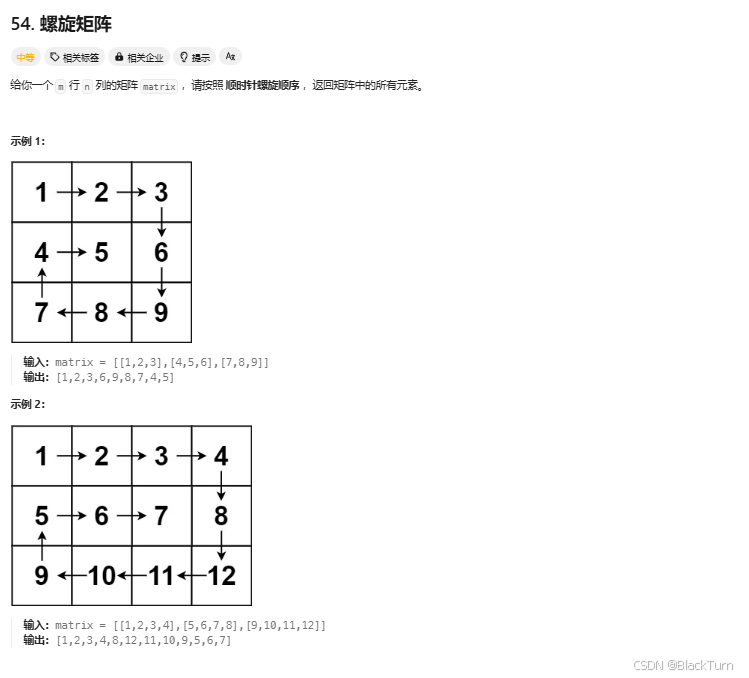
矩阵是:
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
①从左到右遍历,遍历了1->3 用matrix[top][i]其中top是0,而i是0,1,2
②从从上到下遍历,遍历了6->9 用matrix[i][right]其中right是2,而i是1,2
③从右到左遍历,遍历了8->7 用matrix[bottom][i]其中bottom是2,而i是1,0
④从下到上遍历左边,遍历了7->4 用matrix[i][left]其中left是0,而i是2,1
⑤从左到右遍历,遍历了4->5 用matrix[top][i]其中top是1,而i是0,1
public class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> result = new ArrayList<>();
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return result;
}
int rows = matrix.length;
int cols = matrix[0].length;
int left = 0, right = cols - 1;
int top = 0, bottom = rows - 1;
while (left <= right && top <= bottom) {
for (int i = left; i <= right; i++) {
result.add(matrix[top][i]);
}
top++;
for (int i = top; i <= bottom; i++) {
result.add(matrix[i][right]);
}
right--;
if (top <= bottom) {
for (int i = right; i >= left; i--) {
result.add(matrix[bottom][i]);
}
bottom--;
}
if (left <= right) {
for (int i = bottom; i >= top; i--) {
result.add(matrix[i][left]);
}
left++;
}
}
return result;
}
public static void main(String[] args) {
Solution spiralMatrix = new Solution();
int[][] matrix = {
{
1, 2, 3},
{
4, 5, 6},
{
7, 8, 9}
};
List<Integer> result = spiralMatrix.spiralOrder(matrix);
for (int num : result) {
System.out.print(num + " ");
}
}
}
Solution48. 旋转图像
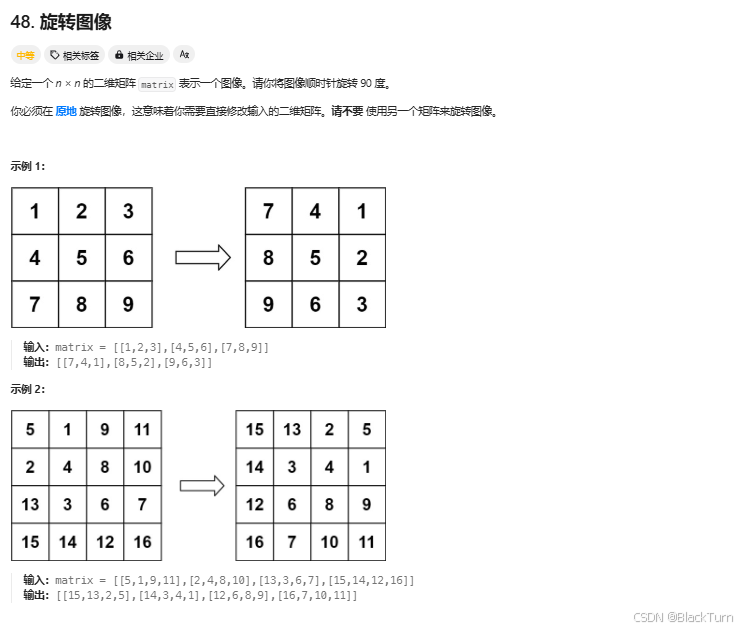
第一步:转置矩阵
将矩阵的行变成列,列变成行。在代码中,通过遍历矩阵的上三角(包括对角线),并交换 matrix[i][j] 和 matrix[j][i] 来实现转置。
1, 2 1, 3
3, 4 转置后变成 2, 4
第二步:反转每一行
遍历每一行,每一行数据都进行反转
1, 3 3, 1
2, 4 每一行反转后变成 4, 2
如此变完成了旋转90度
public class Solution {
public static void main(String[] args) {
int[][] matrix = {
{
1, 2, 3},
{
4, 5, 6},
{
7, 8, 9}
};
rotate(matrix);
for (int[] row : matrix) {
for (int num : row) {
System.out.print(num + " ");
}
System.out.println();
}
}
public static void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
for (int i = 0; i < n; i++) {
int left = 0, right = n - 1;
while (left < right) {
int temp = matrix[i][left];
matrix[i][left] = matrix[i][right];
matrix[i][right] = temp;
left++;
right--;
}
}
}
}
Solution240. 搜索二维矩阵 II

从矩阵的右上角或左下角开始搜索:
从右上角开始搜索时,如果当前元素大于目标值,我们可以向左移动一列(因为左边的元素更小);
如果当前元素小于目标值,我们可以向下移动一行(因为下边的元素更大)。
这样,我们总是朝着可能包含目标值的方向移动,直到找到目标值或搜索到矩阵的边界为止。
public class Solution {
public static void main(String[] args) {
int[][] matrix = {
{
1, 4, 7, 11, 15},
{
2, 5, 8, 12, 19},
{
3, 6, 9, 16, 22},
{
10, 13, 14, 17, 24},
{
18, 21, 23, 26, 30}
};
int target = 5;
boolean result = searchMatrix(matrix, target);
System.out.println("目标值是否存在: " + result);
}
public static boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return false;
}
int m = matrix.length;
int n = matrix[0].length;
int row = 0;
int col = n - 1;
while (row




