当前位置：首页 > news >正文

【深度学习与实战】2.3、线性回归模型与梯度下降法先导案例--最小二乘法(向量形式求解)

news 2025/10/31 19:01:07

为了求解损失函数 $loss = (f(x)-y)^2 = (wx-y)^2$ 对 $w$ 的导数，并利用最小二乘法向量形式求解 $w$ 的值‌

这是‌线性回归‌的平方误差损失函数，目标是最小化预测值 $X_w$ 与真实值 $y$ 之间的差距。

‌损失函数‌：
考虑多个样本的情况，损失函数为所有样本的平方误差之和：

$L = (Xw-Y)^2$

$=( X w-Y )^{\top} ( X w-Y )$

$=w^{\mathsf{T}} X^{\mathsf{T}} X w-Y^{\mathsf{T}} X w-w^{\mathsf{T}} X^{\mathsf{T}} Y+Y^{\mathsf{T}} Y$

$L$ 是损失函数
$X$ 是 $n\times m$ 的设计矩阵（ $n$ 个样本， $m$ 个特征）。
$w$ 是 $m\times 1$ 的权重向量。
$Y$ 是 $n\times 1$ 的目标值向量。
对于两个列向量 $\partial$ 和 $b$ ，它们的点积（内积）就是 $\partial ^Tb$ , $\partial ^T$ 是向量 $\partial$ 的转置

针对 $f(x)$ $=w^{\mathsf{T}} X^{\mathsf{T}} X w-Y^{\mathsf{T}} X w-w^{\mathsf{T}} X^{\mathsf{T}} Y+Y^{\mathsf{T}} Y$ 函数求导，有一下性质：

$\frac{\partial AB}{\partial B} = A^T,\frac{\partial A^TB}{\partial A} = B,\frac{\partial C^TAC}{\partial C} = 2AC$

对每项求导

第一项 $w^{\mathsf{T}} X^{\mathsf{T}} X w$

将 $\frac{\partial C^TAC}{\partial C} = 2AC$ 公式代入得

$X^T \cdot w^T X w$ $\Rightarrow$ $X^T\cdot 2AC$ $\Rightarrow$ $2X^TXw$

$w^{\mathsf{T}} X^{\mathsf{T}} X w$ $= 2X^TXw$

其中 $w^T$ 为 $C^T$ , $X$ 为 $A$ ， $w$ 为 $c$ 。

第二项 $Y^{\mathsf{T}} X w$

将 $\frac{\partial AB}{\partial B} = A^T$ 公式代入得

$Y^{\mathsf{T}} X \cdot w\Rightarrow A^T \Rightarrow (Y^{\mathsf{T}} X)^T$

$Y^{\mathsf{T}} X w = (Y^{\mathsf{T}} X)^T$

其中 $Y^{\mathsf{T}} X$ 为 $A$ , $w$ 为 $B$

第三项 $w^{\mathsf{T}} X^{\mathsf{T}} Y$

将 $\frac{\partial A^TB}{\partial A} = B$ 代入得

$w^{\mathsf{T}} \cdot X^{\mathsf{T}} Y\Rightarrow B\Rightarrow X^{\mathsf{T}} Y$

$w^{\mathsf{T}} X^{\mathsf{T}} Y = X^{\mathsf{T}} Y$

其中 $w^T$ 为 $A^T$ , $X^{\mathsf{T}} Y$ 为 $B$

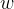第四项没有 $w$ 看作常数项常数项的导数为0

合并项得

$f(x) =w^{\mathsf{T}} X^{\mathsf{T}} X w-Y^{\mathsf{T}} X w-w^{\mathsf{T}} X^{\mathsf{T}} Y+Y^{\mathsf{T}} Y$

$= 2X^TXw-(Y^{\mathsf{T}} X)^T-X^{\mathsf{T}} Y+0$

$=2X^TXw-X^{\mathsf{T}} Y-X^{\mathsf{T}} Y$

$=2X^TXw-2X^{\mathsf{T}} Y$

$=2(X^TXw-X^{\mathsf{T}} Y)$

令 $\frac{\partial f(w)}{\partial w} = 0$ ,得

$2(X^TXw-X^{\mathsf{T}} Y) = 0$

$X^TXw=X^{\mathsf{T}} Y$

$(X^TX)^{-1}X^TXw=(X^TX)^{-1}X^{\mathsf{T}} Y$ （ $X^TX$ 可逆时）

$w=(X^TX)^{-1}X^{\mathsf{T}} Y$

$(X^TX)$ 和 $(X^TX)^{-1}$ 互为逆矩阵 $(X^TX)(X^TX)^{-1} = 1$

得出结果

$w=(X^TX)^{-1}X^{\mathsf{T}} Y$

解释：

$(X^TX)(X^TX)^{-1} = 1$ , $(X^TX)$ 与 $(X^TX)^{-1}$ 互逆

‌逆矩阵的定义

如果 $B$ 是 $A$ 的逆矩阵，则满足：

$AB=BA=I$ (单位矩阵类似于数值乘法中的 1)

即无论 $A$ 左乘还是右乘 $B$ ，结果均为单位矩阵。

必要条件

$A$ 和 $B$ 必须是方阵（行数=列数）

$A$ 必须可逆，矩阵的行列式不为零（即行列式 $det(A) \neq 0$ ）

直观理解

逆矩阵的作用类似于“倒数”。例如，数值中 $2\times \frac{1}{2} = 1$ ，类似地，矩阵中 $A\times A^{-1} = I$ 。

单位矩阵 $I$ 在矩阵乘法中的作用类似于数值乘法中的 1。

示例验证

取矩阵 $A=\begin{bmatrix} 1 & 2 \\ 3& 4 \end{bmatrix}$ ，其行列式 $det(A) = -2 \neq 0$ ，故可逆。

计算逆矩阵：

$A^{-1} = \frac{1}{det(A)}\begin{bmatrix} 4 &-2 \\ -3& 1 \end{bmatrix}= \frac{1}{-2}\begin{bmatrix} 4 &-2 \\ -3& 1 \end{bmatrix}= \begin{bmatrix} -2 &1 \\ \frac{3}{2}& -\frac{1}{2} \end{bmatrix}$