DFS深度优先搜索

DFS是一种暴力的搜索，其核心思想是遍历所有方案，一条路走到黑再进行回溯。存储时只需要存储路径。

例1：按字典序输出1-n的全排列。

这就要求我们做到前面已经用过的数字不再出现，因此我们需要一个state数组来去重并且在回溯时恢复现场。

int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)//u代表当前的层数
{
    if(u > n)//数字填完了，输出
    {
        for(int i = 1; i <= n; i++)//输出方案
            cout << path[i] << " ";
        cout << endl;
        return ；
    }

    for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n
    {
        if(!state[i])//如果数字 i 没有被用过
        {
            path[u] = i;//放入空位
            state[i] = 1;//数字被用，修改状态
            dfs(u + 1);//填下一个位
            state[i] = 0;//回溯，取出 i
        }
    }
}

例2：P1036 [NOIP 2002 普及组] 选数 - 洛谷

在n个数中选出k个数，并且不同顺序的算一种；相比例1的全排列问题，我们要去掉重复的数量。

因此最后结果要除以n的全排列也就是n的阶乘。

void dfs(int u)
{
    if (u==k)//当选完k个数后
    {
        int sum=0;
        for (int i=0; i<k; i++)
        {
            sum+=ans[i];
        }
        if (isprimer(sum))
        {
            c++;
            //cout << sum << ' ';
        }
        
        
        
        return ;
    }
    for (int i=0; i<n; i++)
    {
        if (!b[i])//判断这个数有没有被选过。
        {
            ans[u]=a[i];//选入答案数组中
            b[i]=true;
            dfs(u+1);
            b[i]=false;// 恢复现场

        }
    }
    
    
}

例3：P2404 自然数的拆分问题 - 洛谷

题目可以理解为在1到n这些数中可以重复的选一些数，使其和为n。因此dfs在传参时，可加入一个sum参数。

void dfs(int u,int sum)
{
    if (sum>n)//当sum大于n时，不符合条件直接结束该路径（我也是在输出结果看到不对后才想起来的）
    {
        return ;
    }
    if (sum==n)//符合预期
    {
        int ans[15];
        if (cun[0]==n)
        {
            return ;
        }//剪掉不符合要求的答案
        for (int i=0; i<u-1; i++)
        {
            if (cun[i]>cun[i+1])
            {
                return ;
            }//当出现如1 1 1 1 2 1这种重复答案时，直接剪掉，保留1 1 1 1 1 2
            
            //cun.clear();
        }
        for (int i=0; i<u-1; i++)
        {
            cout << cun[i] << '+';
        }//输出最后答案。
        cout << cun[u-1];
        cout << endl;
        return ;
    }
    for (int i=1; i<=n; i++)
    {
        cun[u]=i;
        dfs(u+1,sum+i);//因为可以重复使用数字，所以无bool数组。
        //cun[u]=0;
    }
}

跟例2一样，全排列带来了重复问题

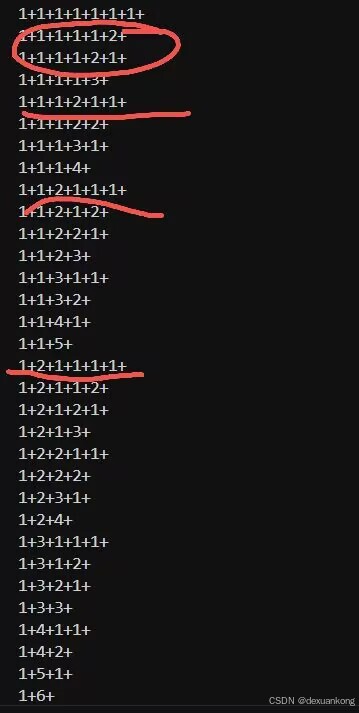
我们只需要判断数组前面的数是否小于后面的数，如果是，就输出。可以有效避免重复问题。