当前位置：首页 > news >正文

力扣热门100题【525，1314】

news 来源：原创 2025/5/1 15:47:08

学习算法LeetCode热门100题

LeectCode 525

525.连续数组https://leetcode.cn/problems/contiguous-array/

1、题目描述

给定一个二进制数组 nums , 找到含有

相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

2、解题思路

主要思想，把0变成-1，然后计算最大区间中的总和是0，计算每个位置的前缀和时，只需要记录每个位置的前缀和和下标，然后在前缀和一样的时候就可以计算最大的长度
数组 0,0,1,0,0,0,1,1
比如在下标是0到1中【0-1】这个2个数中的前缀和是-2，然后【0-3】的前缀和是-2，满足区间【2-3】这个时候我们计算的是3-1=2，区间是2，
当前缀和相同时, 前一个 i1 后面一个位置开始一直到 i2 的区间是满足题目要求的子数组最大区间的计算就是用当前出现的下标-最早出现的下标
哈希表初始化当一个数组中的总和刚刚好是0，比如 0，1，0，1
这个时候hash表中有 [-1，0],[0，1],[-1，2],[0，3]
这个时候我们就是3-1=2 但是不符合，所以必须初始化所以（0，-1）也可以理解当前缀和相同时, 前一个 i1 后面一个位置开始一直到 i2 的区间是满足题目要求的子数组，0在第一个位置，所以她的前一个位置是-1

3、算法代码

class Solution {
     public  int findMaxLength(int[] nums) {
        HashMap<Integer,Integer> hash = new HashMap<>();
        hash.put(0,-1); //初始化
        int ret = 0,sum = 0;
        for (int i = 0; i < nums.length; i++) {

            sum += nums[i] == 0 ? -1:1;
            if (hash.containsKey(sum)){
                int j = hash.get(sum);
                ret = Math.max(ret,i-j);
            }else {
                hash.put(sum,i);
            }

        }
        return ret;

    }
}

4、结果运行

LeetCode.1314 矩阵区域和

点击【1314.矩阵区域和】区域和https://leetcode.cn/problems/matrix-block-sum/description/

1、题目描述

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

2、算法思路

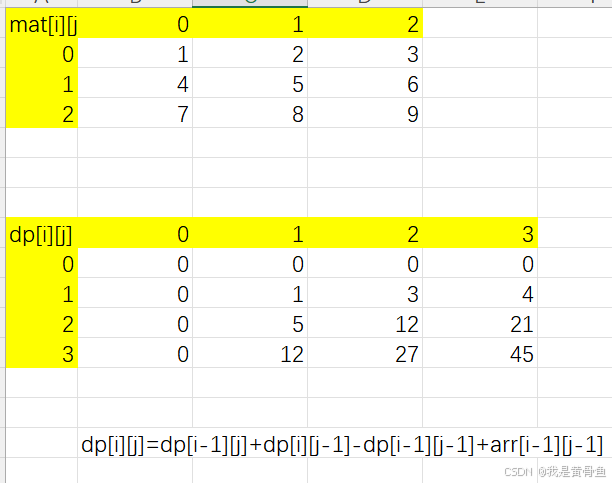
1、先计算前缀和

要计算i，j的前缀和，就要使用绿色+橙色 -蓝色（因为重复减去了2次）+当前位置的值

根据前缀和公式 dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+arr[i-1][j-1]

2、使用前缀和

左上角的(x1,y1)和右下角（x2,y2）围的区域是待求区域，

求得公式 res[i][j] = dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1]

3、理解坐标映射关系

（1）这里是x1=i-k , y1=j-k，x2=i+k,y2=j+k

（2）看成 x1,x2,y1,y2是待求的边界

（3）边界情况,因为是dp映射到ret，所以需要每个坐标+1

Math.max(0,i-k)+1,y1 = Math.max(0,j-k)+1;

Math.min(m-1,i+k)+1,y2 = Math.min(n-1,j+k)+1;

（4）代入公式 res[i][j] = dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1]

3、算法代码

class Solution {
     public  int[][] matrixBlockSum(int[][] mat, int k) {
        //获取前缀和矩阵dp[i][j]
        int m = mat.length,n = mat[0].length;
        int[][] dp = new int[m+1][n+1];
        for (int i = 1;i <= m;i++){
            for (int j = 1;j<=n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1] -dp[i-1][j-1] +mat[i-1][j-1];
            }
        }

        //开始处理
        int[][] ret = new int[m][n];
        for (int i=0;i<m;i++){
            for (int j = 0; j < n; j++) {
                //x和y的坐标指的是dp的坐标，有映射关系所以需要+1
                int x1 = Math.max(0,i-k)+1,y1 = Math.max(0,j-k)+1;
                int x2 = Math.min(m-1,i+k)+1,y2 = Math.min(n-1,j+k)+1;
                //最后按照公式代入
                ret[i][j] = dp[x2][y2]-dp[x1 -1][y2]-dp[x2][y1 -1]+dp[x1 -1][y1 -1];
            }
        }
        return ret;

    }
}