信号与系统笔记——第二章 连续系统的时域分析（三）

2.3 卷积积分

Z2.12 信号的时域分解

1.预备知识

2.任意信号分解

Z2.13 卷积公式

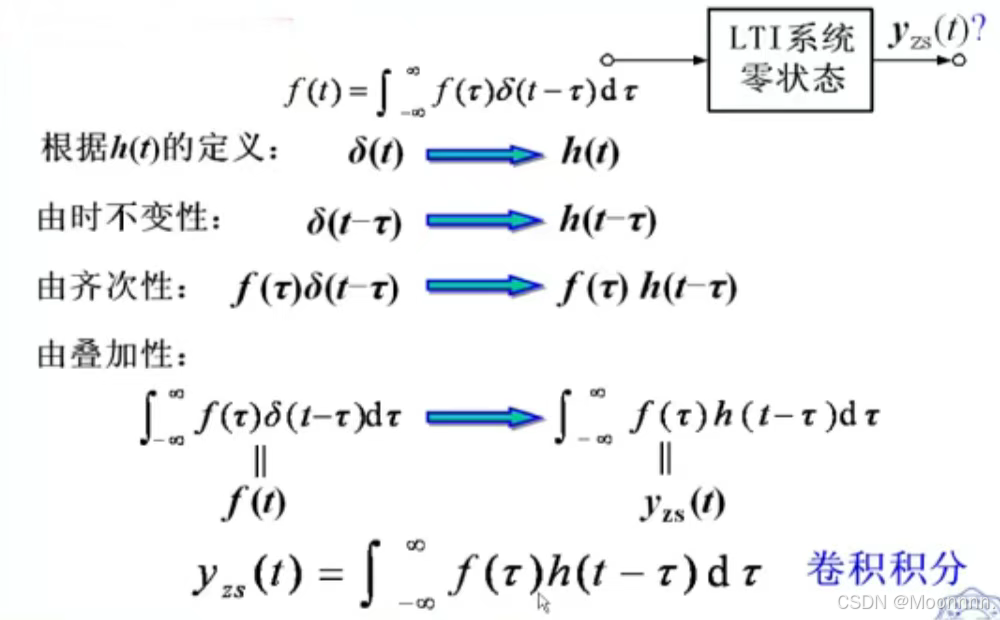
 说明：可演变其他上下限

① ε(t)在t＜0时恒为0，所以不考虑t＜0的时候，积分限为0~＋∞

②ε(t－τ)中t－τ＞0，所以τ＜0，积分限为－∞~t

（f(t)·ε(t)称为因果信号）

Z2.14 卷积积分的图解法

Z2.15 卷积积分的代数性质

1.满足乘法的三律

2.复合系统的冲激响应

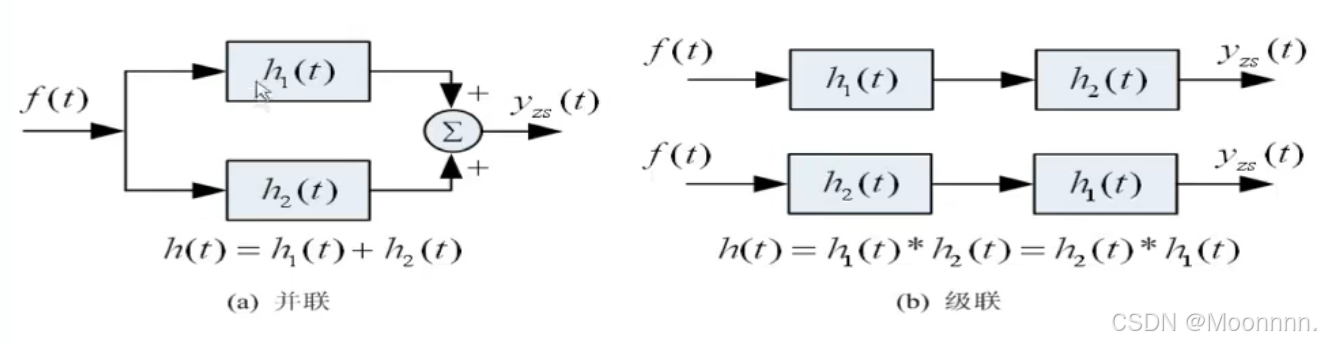
Z2.16 奇异函数的卷积特性

Z2.17 卷积的微积分性质

Z2.18 卷积的时移特性

Z2.19 常用的卷积重要公式

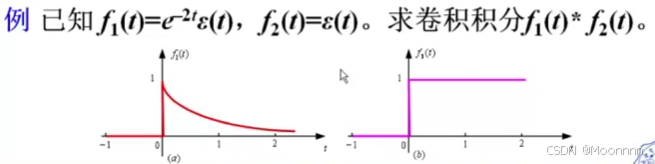
Z2.20 综合举例：卷积的多种求解

求解卷积的方法可归纳为：

1. 利用定义式，直接进行积分。对于容易求积分的函数比较有效。如指数函数，多项式函数等。
2. 图解法。特别适用于求某时刻点上的卷积值。
3. 利用性质。比较灵活。

三者常常结合起来使用。

Z2.21 综合举例：用梳状函数卷积产生周期信号

Z2.22 综合举例：矩形脉冲的卷积产生三角形和梯形脉冲

 

Z2.23 卷积的Matlab求解

MATLAB处理离散卷积的函数为 conv(f1,f2)，对序列做卷积运算。

处理连续信号的卷积时，需要对连续信号取相同的卷积步长，结果再乘以实际步长（连续信号的取样间隔）。

注：本文出自对bilibili 【西安电子科技大学】郭宝龙教授（课程负责：朱娟娟） 信号与系统（第二章） 内容的学习笔记。