Python打卡训练营Day58
DAY 58 经典时序预测模型2
知识点回顾:
- 时序建模的流程
- 时序任务经典单变量数据集
- ARIMA(p,d,q)模型实战
- SARIMA摘要图的理解
- 处理不平稳的2种差分
- n阶差分---处理趋势
- 季节性差分---处理季节性
建立一个ARIMA模型,通常遵循以下步骤:
1. 数据可视化:观察原始时间序列图,判断是否存在趋势或季节性。
2. 平稳性检验:
- 对原始序列进行ADF检验。
- 如果p值 > 0.05,说明序列非平稳,需要进行差分。
3. 确定差分次数 d:
- 进行一阶差分,然后再次进行ADF检验。
- 如果平稳了,则 d=1。否则,继续差分,直到平稳。
4. 确定 p 和 q:
- 对差分后的平稳序列绘制ACF和PACF图。
- 根据昨天学习的规则(PACF定p,ACF定q)来选择p和q的值。
5. 建立并训练ARIMA(p, d, q)模型。
- 模型评估与诊断:查看模型的摘要信息,检查残差是否为白噪声。
- AIC用来对比不同模型选择,越小越好
- 关注系数是否显著,通过p值或者置信区间均可
- 残差的白噪声检验+正态分布检验
7. 进行预测(需要还原回差分前的结构)
作业:对太阳黑子数量数据集用arima完成流程
#太阳黑子数量数据集from statsmodels.datasets import sunspots
df_sun = sunspots.load_pandas().data['SUNACTIVITY']
df_sun.head()df_sun.plot(figsize=(12, 6))#平稳性检验
# 引入ADF检验的函数
from statsmodels.tsa.stattools import adfuller # --- 新增:使用ADF检验来判断平稳性 ---print("开始进行ADF平稳性检验...")# 执行ADF检验
# adfuller()函数会返回一个包含多个结果的元组
adf_result = adfuller(df_sun)# 提取并展示主要结果
adf_statistic = adf_result[0]
p_value = adf_result[1]
critical_values = adf_result[4]print(f"ADF统计量 (ADF Statistic): {adf_statistic:.4f}")
print(f"p值 (p-value): {p_value:.4f}")
print("临界值 (Critical Values):")
for key, value in critical_values.items():print(f' {key}: {value:.4f}')print("\n--- 检验结论 ---")
# 根据p值进行判断
if p_value < 0.05:print(f"p-value ({p_value:.4f}) 小于 0.05,我们强烈拒绝原假设(H₀)。")print("结论:该序列是平稳的 (Stationary)。")
else:print(f"p-value ({p_value:.4f}) 大于或等于 0.05,我们无法拒绝原假设(H₀)。")print("结论:该序列是非平稳的 (Non-stationary)。")# 也可以通过比较ADF统计量和临界值来判断,结论是一致的
if adf_statistic < critical_values['5%']:print("\n补充判断:ADF统计量小于5%的临界值,同样表明序列是平稳的。")
#--- 检验结论 ---
# p-value (0.0531) 大于或等于 0.05,我们无法拒绝原假设(H₀)。
# 结论:该序列是非平稳的 (Non-stationary)。import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
# 中文显示设置
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示为方块的问题
#差分
df_sun_diff = df_sun.diff().dropna()
plt.plot(df_sun_diff)
plt.title('一阶差分后的数据')
plt.show()
# 一阶差分后的ADF检验
adf_result_diff = adfuller(df_sun_diff)
print(f'一阶差分后数据的ADF检验结果:')
print(f' ADF Statistic: {adf_result_diff[0]}')
print(f' p-value: {adf_result_diff[1]}') # p-value会变得非常小,说明数据变平稳了
# d = 1# 绘制ACF和PACF图
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
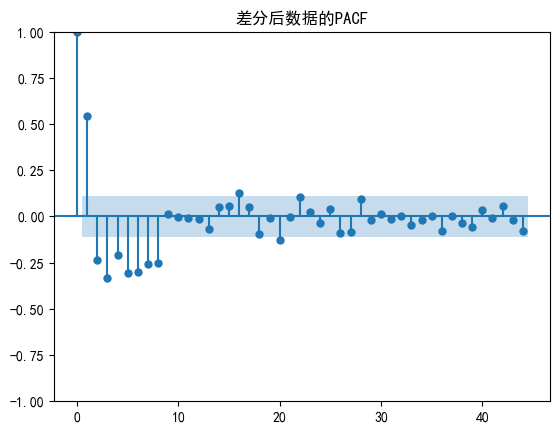
plot_pacf(df_sun_diff, lags=44)
plt.title('差分后数据的PACF')
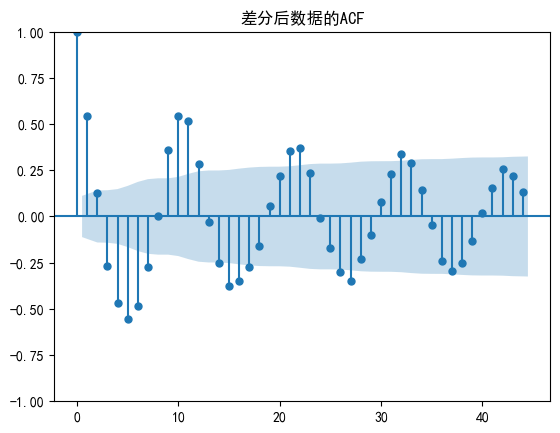
plt.show()plot_acf(df_sun_diff, lags=44)
plt.title('差分后数据的ACF')
plt.show() #p 8 ; q 1 or 0from statsmodels.tsa.arima.model import ARIMA
import warnings
warnings.filterwarnings("ignore")
# 建立ARIMA模型
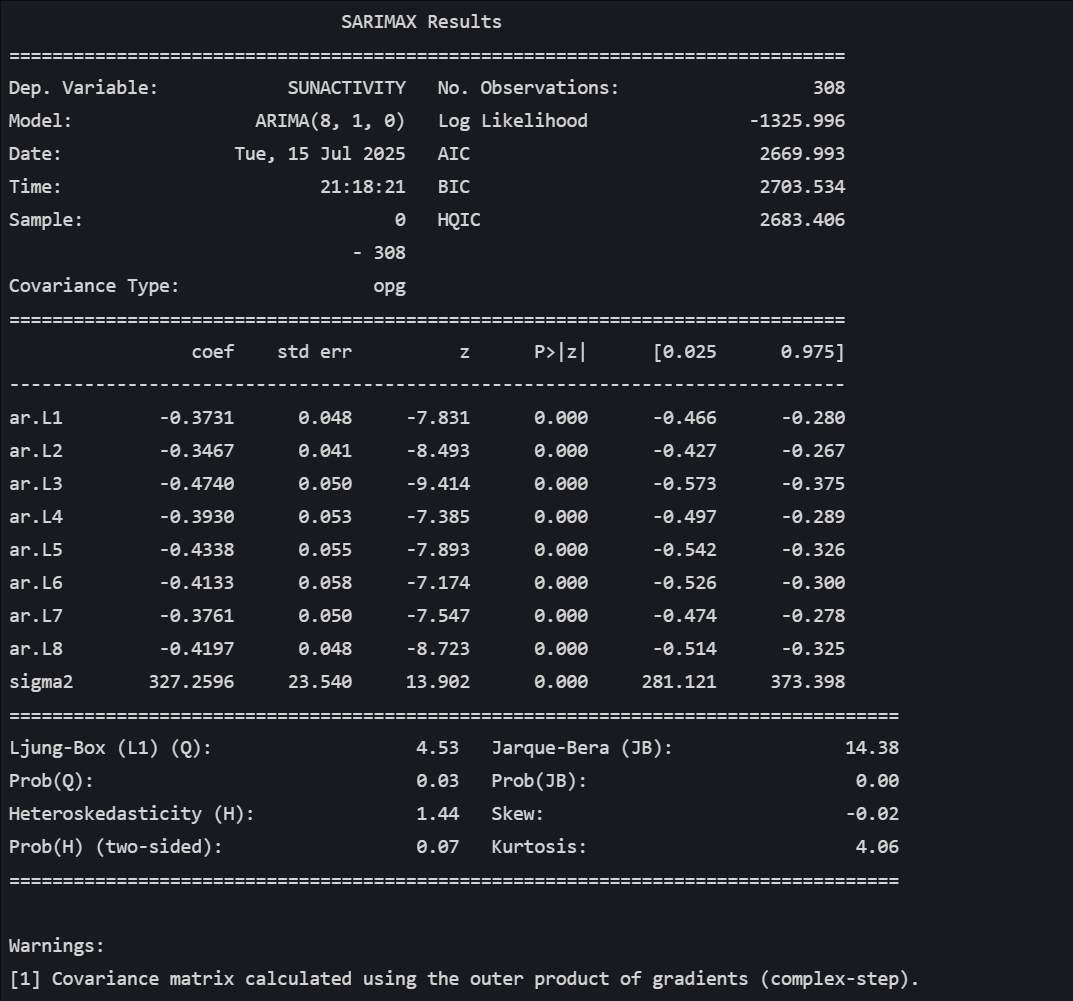
model = ARIMA(df_sun_diff, order=(8, 1, 0))
arima_result = model.fit()# 打印模型摘要
print(arima_result.summary())# 让我们预测未来33年
forecast_steps = 33
forecast = arima_result.get_forecast(steps=forecast_steps)
pred_mean = forecast.predicted_mean
conf_int = forecast.conf_int()# 绘制结果
plt.figure(figsize=(14, 7))
plt.plot(df_sun_diff, label='原始数据')
# 绘制模型在历史数据上的拟合值
plt.plot(arima_result.fittedvalues, color='orange', label='模型拟合值')
# 绘制未来预测值
plt.plot(pred_mean, color='red', label='未来预测值')
# 绘制置信区间
plt.fill_between(conf_int.index,conf_int.iloc[:, 0],conf_int.iloc[:, 1], color='pink', alpha=0.5, label='95%置信区间')
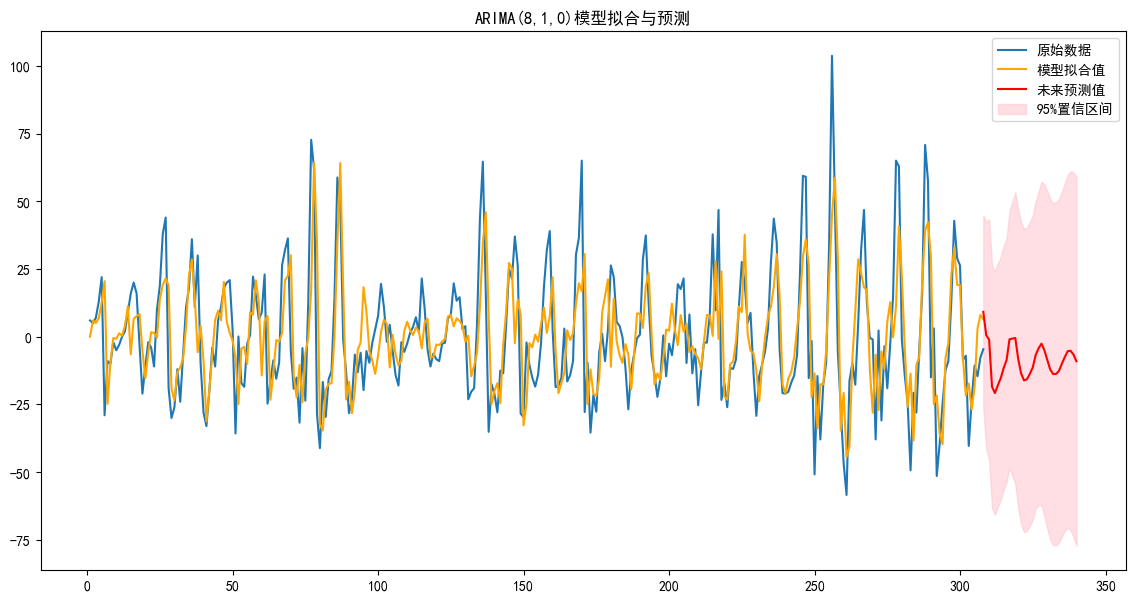
plt.title('ARIMA(8,1,0)模型拟合与预测')
plt.legend()
plt.show()
#核心看点:AIC 和 BIC。当你在比较不同模型时(比如 ARIMA(2,0,0) vs ARIMA(1,0,1)),这两个值是选择“最佳”模型的重要依据。