考虑频率耦合的构网型（GFM）VSG变流器（电压电流双闭环控制结构）的二维序阻抗与降维SISO序阻抗建模详细推导及扫频对比验证

目录

1、课程及模型介绍

2、构网型VSG变流器拓扑结构及控制策略

3、构网型VSG变流器阻抗建模思路及详细推导

3.1 谐波线性化建模原理及降维SISO等效阻抗建模思路

3.1.1 谐波线性化建模及典型正负序阻抗建模

3.1.2 频率耦合原理及二维耦合阻抗定义

3.1.3 构网型VSG变流器降维SISO等效序阻抗建模的核心思路

3.2 构网型VSG变流器降维SISO等效阻抗建模详细推导

3.2.1 构网型VSG变流器功率环建模及主电路核心方程

3.2.2 VSG有功外环的小干扰频域表达式推导

3.2.3 VSG无功外环的小干扰频域表达式推导

3.2.4 电压电流双闭环输出调制函数的小干扰频域表达式推导

3.2.5 构网型VSG变流器端口二维耦合序阻抗求解

3.2.6 构网型VSG变流器端口降维SISO等效序阻抗求解

4、构网型VSG变流器降维SISO等效序阻抗验证及对比

4.1 阻抗扫频测量思路和流程

4.2 算例模型及扫频对比

5、小干扰稳定性专栏出版声明

6、文章版权声明

参考文献

1、课程及模型介绍

本人为985院校电气强校博士，主要研究方向：新能源发电并网系统、电力电子化电力系统稳定控制等。

当前，应用于新能源发电场景的并网逆变器以跟网型（Grid-Following, GFL）为主。该类型逆变器依赖锁相环（Phase-Locked Loop, PLL）实时采集并网点（Point of Common Coupling, PCC）的相位信息，实现与电网的同步运行，功率跟踪性能以及动态响应速度较好。然而，在弱电网环境下，受系统强度不足、物理惯量较低、装机规模增大等因素影响，跟网型并网系统存在小干扰振荡失稳问题[1]。在此背景下，采用虚拟同步发电机（Virtual Synchronous Generator, VSG）控制策略的构网型（Grid-Forming, GFM）逆变器成为主流方案[2-4]。此类逆变器通过模拟同步发电机的外特性，为电力系统注入惯性支撑与阻尼特性，能够维持电网电压和频率的动态稳定，因而在电网强度弱、惯量支撑能力不足的场景中得到了广泛应用。

文献[5-6]指出除了跟网型系统，构网型VSG系统也存在频率耦合效应，阻抗表现为单输入双输出特性，即在PCC点注入某一频率的电压扰动激励，除了产生想通频率的电流响应外，还会产生二倍频耦合频率的电流响应分量，采用谐波线性化方法建立的输出阻抗模型表现为2×2的矩阵形式，并通过端口网络等效电路获取降维（Single in and single out，SISO）等效序阻抗模型。

本文为小干扰稳定性系列文章中的第十二篇，是第八篇文章（关于构网型VSG变流器正负序阻抗建模）的延伸与拓展，建立了基于VSG级联电压电流双闭环控制系统的构网型VSG变流器降维SISO等效序阻抗模型并通过扫频进行验证。其次，通过与构网型VSG变流器正负序阻抗特性进行对比分析，说明降维SISO等效序阻抗模型的精度优于正负序阻抗模型。 本文所复现/参照的文献包含但不限于[1-12]。

小干扰稳定性分析的基础是小干扰稳定性模型，小干扰稳定性模型的精确度决定了小干扰稳定性判定结果的准确性。小干扰稳定性分析系列文章中的第一篇、第二篇、第三篇详细讲解了跟网型VSC变流器序阻抗建模原理、谐波线性化理论推导以及新能源发电并网系统小干扰稳定性分析、控制交互作用分析、主导参数/变流器分析、宽频振荡复现等内容；小干扰稳定性分析系列文章中的第八篇、第九篇、第十篇详细讲解了构网型VSG变流器序阻抗建模原理、谐波线性化理论推导以及新能源发电并网系统小干扰稳定性分析、控制交互作用分析、主导参数/变流器分析、宽频振荡复现等内容；小干扰稳定性分析系列文章中的第十一篇对比分析了构网型VSG变流器及跟网型VSC变流器并网系统强弱电网工况下小干扰/动态/振荡稳定性。以上文章建议在学习本文章后一并学习，夯实基础，更加系统、深入掌握多元化新能源并网系统小干扰稳定性学术理论体系。

系列第一篇（全文链接：基于谐波线性化方法的跟网型GFL并网变流器/VSC宽频序阻抗建模及扫频（Matlab/Simulink平台）及文献复现-CSDN博客文章浏览阅读1.9w次，点赞101次，收藏210次。本人为985院校电气工程博士在读，研究方向为新型电力系统小干扰稳定性分析。该文章重点讲解基于谐波线性化方法的跟网型并网逆变器/VSC宽频序阻抗建模及扫频（Matlab/Simulink平台）原理及实现。目的在于，尽我所学，将晦涩繁琐的理论公式通过通俗易懂的方式讲解清楚原理本质，让看似“高门槛”的阻抗建模理论知识更加容易理解学习，与各位初学者和同行进行学术分享，希望对大家有所帮助，不足之处也欢迎大家多多批评指正。欢迎留言交流探讨。_谐波线性化https://blog.csdn.net/2401_82983656/article/details/136102314

系列第二篇（全文链接：新能源发电并网系统/新型电力系统小干扰稳定性分析/宽频振荡复现（频域阻抗分析法/时域模态分析法/仿真分析法）_dq变换控制和弱电网-CSDN博客文章浏览阅读1.1w次，点赞60次，收藏139次。本人为985院校电气工程博士在读，研究方向为新型电力系统小干扰稳定性分析。该文章重点讲解新能源发电并网系统/新型电力系统小干扰稳定性分析方法/宽频振荡复现（频域阻抗分析法/时域模态分析法/仿真分析法）。目的在于，尽我所学，将晦涩繁琐的理论公式通过通俗易懂的方式讲解清楚原理本质，让看似“高门槛”的小干扰稳定性理论更容易理解学习，与各位初学者和同行进行学术分享，希望对大家有所帮助，不足之处也欢迎大家多多批评指正。欢迎留言交流探讨。各位如果有需要获取本文章中涉及的代码和模型，可联系QQ：2293540475。_dq变换控制和弱电网https://blog.csdn.net/2401_82983656/article/details/136106081

系列第三篇（全文链接：

基于阻抗灵敏度/参数灵敏度的新能源发电并网系统/新型电力系统小干扰稳定性分析、稳定性主导因素分析、控制交互作用特性及机理分析_新型电力系统阻尼特性分析-CSDN博客文章浏览阅读2.8k次，点赞34次，收藏31次。本人为985院校电气工程博士在读，研究方向为新型电力系统小干扰稳定性分析。本文为小干扰稳定性分析系列文章中的第三篇，重点讲解基于阻抗灵敏度/参数灵敏度的新能源发电并网系统/新型电力系统小干扰稳定性分析、稳定性主导因素分析、控制交互作用特性及机理分析，作为小干扰稳定性分析的拓展延伸和应用开发，可用于主导参数提取、主导变流器筛选、振荡溯源等方面研究。qq联系：2293540475_新型电力系统阻尼特性分析https://blog.csdn.net/2401_82983656/article/details/139389768系列第八篇（全文链接：考虑频率耦合的构网型VSG变流器（电压电流双闭环控制结构）序阻抗建模扫频及中英文顶刊文献复现（Matlab&Simulink等）适用于弱网稳定性分析、跟网构网混合并网等场景-CSDN博客文章浏览阅读1.2w次，点赞59次，收藏123次。本人为985院校电气工程博士在读，研究方向为新型电力系统小干扰稳定性分析，全部文章、模型代码均为本人原创。该文章讲解基于谐波线性化方法的构网型VSG型变流器宽频序阻抗建模及扫频（Matlab/Simulink平台）原理及实现。目的在于，尽我所学，将晦涩繁琐的理论公式通过通俗易懂的方式讲解清楚原理本质，让看似“高门槛”的阻抗建模理论知识更加容易理解学习，与各位初学者同行进行学术分享，希望对大家有所帮助，不足之处也欢迎大家多多批评指正。欢迎留言交流探讨。_构网型vsghttps://blog.csdn.net/2401_82983656/article/details/140173772

系列第九篇（全文链接构网型VSG新能源并网系统强弱电网小干扰/动态/振荡稳定性分析及仿真算例验证（高比例大规模新能源并网场景）_vsg电气图-CSDN博客文章浏览阅读4.5k次，点赞23次，收藏55次。本人为985院校电气工程博士在读，方向为小干扰稳定性分析，全部文章、模型代码均为本人原创。本文讲解基于阻抗法的构网型VSG变流器并网系统小干扰稳定性分析。目的在于，尽我所学，将晦涩繁琐的理论公式通过通俗易懂的方式讲解清楚原理本质，让看似“高门槛”的小干扰稳定性理论知识更加容易理解学习，与各位初学者和同行进行学术分享，希望对大家有所帮助，不足之处也欢迎大家多多批评指正。欢迎留言交流探讨。各位如果有需要获取本文章中涉及的代码和模型，可联系QQ：2293540475。_vsg电气图https://blog.csdn.net/2401_82983656/article/details/140219611

系列第十篇（全文链接：基于阻抗灵敏度/参数灵敏度的构网型VSG新能源发电并网系统稳定性主导因素分析、控制交互/耦合作用特性及机理分析_构网vsg并机无限-CSDN博客文章浏览阅读2.2k次，点赞26次，收藏21次。本人为985院校电气工程博士在读，方向为小干扰稳定性分析，全部文章、模型代码均为本人原创。本文基于阻抗灵敏度/参数灵敏度的构网型新能源发电并网系统/新型电力系统小干扰稳定性分析、稳定性主导因素分析、控制交互作用特性及机理分析，作为小干扰稳定性分析的拓展延伸和应用开发，可用于主导参数提取、主导变流器筛选、振荡溯源等方面研究。欢迎留言交流探讨。_构网vsg并机无限https://blog.csdn.net/2401_82983656/article/details/142307947

系列第十一篇（全文链接：构网型VSG及跟网型VSC多元化新能源并网系统强弱电网工况下小干扰/动态/振荡稳定性对比分析及仿真算例验证（高比例大规模新能源并网场景）_电力系统vsc-CSDN博客文章浏览阅读5.3k次，点赞21次，收藏44次。本人为985院校电气工程博士在读，方向为小干扰稳定性分析，全部文章、模型代码均为本人原创。本文对比分析当前两种最主流新能源并网系统（跟网型并网及构网型并网）的小干扰稳定性，提供稳定性问题的解决方案。目的在于，尽我所学，将晦涩繁琐的理论公式通过通俗易懂的方式讲解清楚原理本质，让看似“高门槛”的小干扰稳定性理论知识更加容易理解学习，与各位初学者和同行进行学术分享，希望对大家有所帮助，不足之处也欢迎大家多多批评指正。欢迎留言交流探讨。_电力系统vschttps://blog.csdn.net/2401_82983656/article/details/141830453

本文利用谐波线性化方法精确解析具有谐波耦合特性及复杂控制环节的构网型VSG变流器系统动态特性，建立高精度的降维等效序阻抗模型，将建模过程逐步推导、将建模步骤详尽细化、将建模原理挖深吃透，使得当前新型电力系统场景下应用广泛的构网型VSG变流器降维等效序阻抗建模更加容易学习、理解与掌握，希望对大家有所帮助，不足之处也欢迎大家多多批评指正。

欢迎留言交流探讨。各位如果有需要获取本文章中涉及的代码和模型，可联系QQ：2293540475。

2、构网型VSG变流器拓扑结构及控制策略

图1为构网型VSG变流器拓扑结构图。如图1所示，Udc为VSG直流侧电压，直流侧电容较大直流电压维持稳定，此时Udc可视为常数；eabc为构网型VSG变流器输出内电势；Ivabc是变流器输出电流；Igabc为并网电流；vgabc为变流器输出端电压；Lf、Cf、Rf分别为滤波电感、滤波电容和阻尼电阻；Lg为电网电抗；vgird为电网电压。

图2为基于虚拟同步机VSG控制的构网型VSG变流器控制框图。如图2所示，构网型VSG控制器将有功功率指令作为虚拟同步发电机模型的功率指令，使VSG具备惯性和一次调频特性；通过发电机模型中的虚拟惯量和下垂系数产生虚拟同步频率θv，然后通过励磁调节器模型生成虚拟电压幅值Em，使VSG具备一次调压特性。最后将同步频率和励磁电压幅值作为VSG的虚拟内电势指令。本文的虚拟同步VSG控制策略增加了电压电流双闭环级联控制环节[12]，并将虚拟内电势作为级联电压控制回路的参考电压，采用电压电流双闭环控制的输出作为调制环节的电压参考信号。相比于传统开环型PWM信号控制方式下的VSG控制策略[1]，可嵌入电压和电流的饱和限制控制，电压电流双闭环控制环节不仅改变了VSG的输出端电压，还可以加快系统的响应速度。 

​​​

图1 构网型VSG变流器拓扑结构

​​​

图2 构网型VSG变流器控制电路框图

3、构网型VSG变流器阻抗建模思路及详细推导

3.1 谐波线性化建模原理及降维SISO等效阻抗建模思路

3.1.1 谐波线性化建模及典型正负序阻抗建模

小扰动稳定性关注系统对微小扰动的响应,通常采用线性化分析方法。当采用谐波线性化方法进行序阻抗建模时，其基本思路是通过对系统的激励叠加一系列频率处的谐波扰动，忽略扰动项的二次及更高次部分，仅保留其一次项线性部分。常量/常系数一阶幂级数展开后的小信号扰动均为0。谐波线性化方法本质上是在稳态工作点处对模型进行一阶幂级数展开。例如，对变量a进行线性化展开为：a=A+∆a，其中A为a的稳态工作点，∆a为a的一阶小信号扰动量。

在对三相变流器型电源进行建模时，可采用对称分量法，将三相变流器型电源分解为正负序子系统，分别注入正序、负序电压扰动信号（一般采用串联电压扰动源注入的形式，相比于并联电流扰动源注入的形式计算精度更高），得到扰动频率处电流响应，建立构网型VSG变流器在abc坐标系下的正序、负序阻抗模型（Zvsg_p、Zvsg_n）。构网型VSG变流器交流并网系统构成的小信号等效电路如图3所示。

​​

（a）注入正序扰动

​​

（b）注入负序扰动

图3 构网型VSG变流器正负序小信号等效电路

根据图3，对于相位域并网系统，并网点电流Ig的表达式如式(7)所示：

​​（1）

其中，Tm代表前向通道增益为1，负反馈通道增益为Zg(s)/Zvsg(s)的负反馈控制系统系统，其中Zg(s)/Zvsg(s)为系统阻抗比。小干扰稳定性状态主要取决于并网电流Ig的稳定性，Ig的稳定性取决于Tm的稳定性，Tm是否稳定取决于Zg(s)/Zvsg(s)是否满足Nyquist稳定判据。因此，VSC的阻抗建模是小干扰稳定性分析的基础，采用序阻抗模型可简化稳定性分析，并且具有明确的物理意义。需要注意的是，正负序系统均满足稳定判据时说明系统稳定；并网系统中的子系统独立运行时均稳定，系统不存在右半平面极点，因此，在进行稳定性分析时，无需考虑右半平面极点的影响，只关注互联系统阻抗比。

对于三相系统，采用谐波线性化的方法将VSC输出阻抗分解为正负序分量，建立其正负序阻抗模型。而三相系统仅相位各差120°，B，C相输出阻抗与A相相同，因此以A相为例建立构网型VSG变流器序阻抗模型。电网侧注入电压扰动vpa，叠加于稳态工作点，构网型VSG变流器的A相主电路等效小信号电路如图4所示：

​​

图4 构网型VSG变流器A相扰动频率主电路等效小信号电路

由图4可知，根据谐波线性化建模思想，给定扰动电压源为vp注入VSG三相系统，可得到扰动频率处的响应电流。可将图4中的时域变量通过傅里叶变换原理转换到频域下，包含基频分量、扰动序分量，以Iga和Vpa为例：

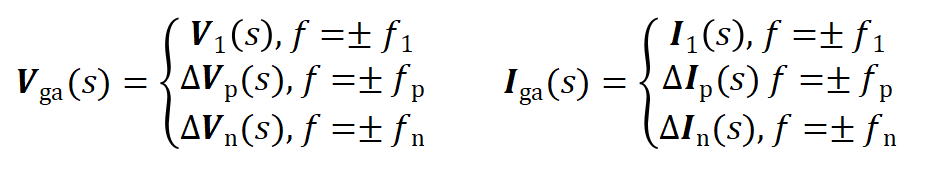​​ （2）

式(8)中，以注入正序扰动电压Vp为例，根据欧拉变换原理，Vp的频域表达式为：

​​（3）

构网型VSG变流器的典型正、负序阻抗Zvsc(s)的计算式为（对变量进行加粗处理，代表该变量的矩阵形式）：

​​（4）

式（4）中，计算的是扰动频率wp处系统端口单维阻抗模型。如果将扰动频率wp处的扰动电压和电流响应换成其他耦合频率处的电压电流量，则可以计算端口多维阻抗矩阵。

文献[1]指出，阻抗矩阵的主对角元素/自阻抗元素在小干扰稳定性分析中起主导作用，若研究对象为三相对称、电流环对称系统，可不考虑频率耦合对VSG序阻抗模型的影响。若专门研究频率耦合效应，则可考虑并网电压、并网电流的扰动分量与二倍频耦合分量的关系，计算系统的耦合阻抗，下一节将重点讲解。

3.1.2 频率耦合原理及二维耦合阻抗定义

大量文献表明[2-10]，当在PCC点注入频率为fp/fn的正序/负序扰动激励电压源，会产生扰动频率fp处的正序/负序扰动电流响应以及关于镜像二倍频（fp-2f1或fn+2f1）处的耦合电流响应，该效应被称为频率耦合效应。图5展示了以dq轴为坐标系的控制系统产生频率耦合的机理示意图（sp=j2πfp、s1=j2πf1）。park正反变换为引入频率耦合的直接原因，根本原因为控制不对称，控制不对称程度越高则频率耦合程度越高，机理的相关阐述详见本人小干扰稳定性系列文章中的第一篇。对于跟网型变流器，dq轴不对称的锁相环、直流电压外环、额外引入dq轴不对称的附加阻尼控制环节均为引起频率耦合的因素。对于构网型VSG变流器，vsg有功环与无功环不对称、额外引入dq轴不对称的附加阻尼控制环节均为引起频率耦合的因素。

图5 dq轴控制系统频率耦合关系示意图 

以正序扰动注入为例，给出图6所示的新能源变流器的频率耦合特性关系图（sp=j2πfp、s1=j2πf1），其中∆Vp(s)为电压扰动，∆Ip(s)为电流响应，Zvsg_pp(sp)、Zvsg_pn(sp)、Zvsg_np(sp)和Zvsg_nn(sp)为构网型VSG变流器二维耦合阻抗矩阵的各元素，Zgsp)为电网阻抗。从图4中可以看出，当在PCC点注入频率为fp的正序扰动电压激励，由于控制不对称作用下的频率耦合效应，系统同时产生扰动频率fp的正序响应电流∆Ip(sp)和频率为fp-2f1的负序耦合电流∆In(sp-2f1)，值得注意的是，此时的耦合电流相位呈现负序特性，并不是指正负序耦合而仍指的是频率耦合，正负序耦合的实际含义见文献[10]。导致系统存在二倍频频率耦合效应的主导因素为：1) PLL；2) d、q轴不对称结构/参数值的电流控制器；3) 直流母线电压控制器；4) 有功和无功控制器；5) 凸极同步电机。由于电网阻抗Zg(s)的存在，并且电网是频率解耦系统，扰动频次和耦合频次的输出电流响应在Zg(s)上分别产生相对应频率的电压扰动分量∆Vg(sp)和∆Vg(sp-2f1)，其中∆Vg(sp)=∆Vp(sp)+Zg(sp)∆Ip(sp)，并通过控制环路及主电路的电压电流关系（阻抗特性）产生扰动频次和耦合频次的电流，闭环系统始终存在扰动频率和耦合频率的谐波量。 

图6 新能源变流器频率耦合特性关系图 

由于频率耦合效应的存在，在描述新能源变流器的端口阻抗特性时，应采用2×2的输出阻抗矩阵，如式（5）所示：

（5）

式中，下标p和n分别表示正序和负序。主对角线元素反映的是某一频率扰动电压对相同频率电流响应的影响程度，非对角线元素反映的是某一频率的扰动电压对耦合频率电流响应的影响程度。 

3.1.3 构网型VSG变流器降维SISO等效序阻抗建模的核心思路

① 根据构网型VSG变流器主电路拓扑结构和VSG级联电压电流控制内环控制原理，根据PWM调制、电容和开关器件动态，建立扰动频率及耦合频率的构网型VSG变流器时域主电路核心方程（非线性模型），即获得构网型VSG变流器的内电势、输出端电压和输出电流的关系。在考虑频率耦合效应条件下，VSG输出电压和电流将同时叠加扰动频率分量和耦合频率分量，主电路等效小信号电路可分解为扰动频率等效电路和二倍频耦合频率等效电路。扰动频率及耦合频率的主电路核心方程来源于图4所示的A相扰动频率主电路等效小信号电路以及下图7所示的A相耦合频率主电路等效小信号电路。

 

图7 构网型VSG变流器A相耦合频率主电路等效小信号电路

② 对构网型VSG变流器模型进行稳态仿真或数值计算，可计算得到系统稳态工作点，作为后续小干扰阻抗求解过程中小信号叠加的稳态运行轨迹。

③ 利用谐波线性化思想，对构网型VSG变流器时域主电路核心方程（非线性模型）进行线性化处理，得到构网型VSG变流器频域线性化核心数学方程（线性化模型）。

④ 针对VSG级联电压电流控制内环控制结构，基于采样得到的小信号电气量，从输入至输出遍历控制系统小信号通路/小信号传递关系得到扰动频率及耦合频率的调制参考电压小信号后，代入构网型VSG变流器频域线性化核心数学方程（线性化模型）进行计算，进一步结合端口二维阻抗矩阵表达式（式（5））可求解得到VSG级联电压电流控制内环下构网型变流器二维序阻抗模型。

⑤  根据图9所示的构网型并网系统双端口网络等效电路（其中Zvsg_pn为由①至④推导获得的构网型变流器二维序阻抗矩阵，Zg_pn为电网正负序阻抗矩阵，下标“equi”表征考虑扰动频率和耦合频率的完整等值量），结合双端口方程及边界条件，通过将表征频率耦合效应的Zvsg_pn和Zvsg_np考虑到VSG的输出序阻抗，可将二维MIMO模型转化为SISO等效模型，计算得到保留频率耦合效应的正负序降维SISO阻抗（Zvsg_equi_p、Zvsg_equi_n）表达式如式（6），具体推导过程见文献[9]。

图8 构网型并网系统双端口网络等效电路

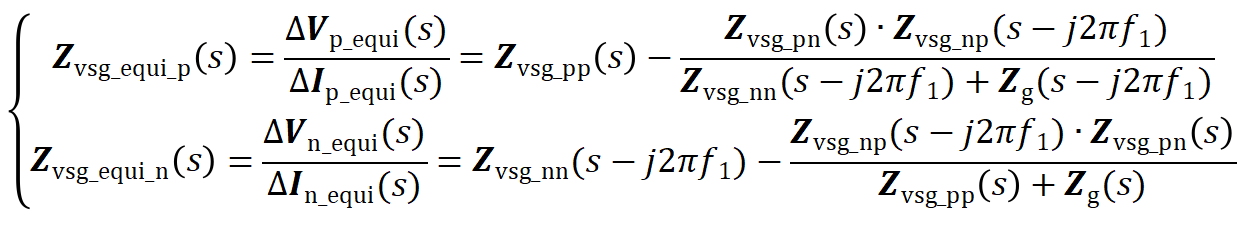
（6）

由文献[7]可知，正负序阻抗之间可相互转化，即正序阻抗等价于相反频率的负序阻抗取共轭，具体表达式为：

（7）

式中：上标“*”表示共轭运算。

根据上述分析可知，正序/负序三相扰动量fp/fn经过Park坐标变换为dq域下扰动量时，在d-q坐标系下的小信号频率产生了偏移，即频率偏移效应，此时小信号频率为fp-fpll/fn+fpll，fp+fpll频次/fn-fpll频次的谐波分量三相对称抵消。如果忽略相角小信号扰动时，此时dq坐标系下小信号频率为fp-f1/fn+f1，对于基频电气量，经过dq变换后小信号频率为f1-f1=0，因此基频电气量在dq域下被转换为了直流分量，因此获得直流稳态工作点。

值得注意：

（1）此时的负序阻抗指的是耦合频率下的等值阻抗，本文以正序扰动注入下的扰动响应分量（下标p）和频率耦合响应分量（下标n，此时的n并非代表注入负序扰动，仅为序分量意义）进行计算求解SISO等效阻抗的过程为例进行讲解，注入负序阻抗下的SISO等效阻抗模型求解过程同理。正负频率变量中均包含了一个频率成分的所有信息，因此下文仅给出正频率分量。上标^和∆均表示小信号量，两者没差别。

（2）计算端口正序、负序阻抗时，正序、负序谐波扰动是单独注入的，正序、负序阻抗是单独求解的，推导过程中注意不要把正序、负序扰动信号与频率耦合特性混淆。举个例子，计算正序阻抗时，频率耦合效应会产生基频偏移信号（dq坐标系）、二倍频耦合信号（abc坐标系），即使频率耦合量是负序的，也是频率耦合量，而非正负序耦合量。正负序耦合特性是由三相主电路不对称产生的，频率耦合特性是由于控制不对称引起的，正负序耦合特性与频率耦合特性有本质上的区别。

关于频率偏移效应、二倍频频率耦合效应、Park变换/反变换小信号线性化等的具体推导证明过程可参考本系列第一篇文章。

3.2 构网型VSG变流器降维SISO等效阻抗建模详细推导

3.2.1 构网型VSG变流器功率环建模及主电路核心方程

根据图2所示的构网型VSG变流器的控制框图，VSG的有功和无功功率控制回路可以分别模仿实际SG的机械部分和电气部分的运行原理。并对VSG的有功和无功控制器的数学模型进行推导。在有功-频率环节的控制下，VSG不仅能够为系统提供惯性和阻尼支持，同时也能利用其与系统频率的偏差参与系统频率调节，为系统提供有功功率支撑。无功-电压控制环节通过无功调压系数Dq来模拟同步发电机的一次调压功能，通过调节无功功率改变内电势，为电网电压提供支撑。VSG的有功和无功控制器的数学模型可以表示为如下形式：

​​ ​

（8）

其中：

​​ ​ （9）

​​ ​ （10）

其中，θv为VSG内电势相位，Tj（J，下文中用J代表Tj）和K分别为虚拟转动惯量和电压系数；ωv和ωn分别为VSG的输出角频率和电网的额定角频率；Tset和T分别为参考转矩和电磁转矩；Dp和Dq分别为阻尼系数和电压下垂系数；Pref和Qref分别是有功功率和无功功率的参考值；P和Q分别是有功功率和无功功率；|V|ref、|V|、Em分别为额定电压、输出电压和内电势的幅值。

根据瞬时功率理论，VSG的瞬时输出有功功率P和无功功率Q可以计算为：

​​ ​（11）

其中，vd和id分别为d轴输出电压和电流，vq和iq分别为q轴输出电压和电流。

VSG的调制波由有功和无功功率环决定，电压调制波信号可以表示为：

​​ ​（12）

其中ea、eb和ec为VSG的三相调制波，起到主电路与控制电路之间的桥梁纽带作用。

根据图4所示的等效电路，结合KCL和KVL定律，可计算得到表征扰动频率下的构网型VSG变流器的内电势、输出端电压和输出电流之间关系的频域主电路核心方程为：​​​（13）

根据图7所示的等效电路，结合KCL和KVL定律，可计算得到表征耦合频率下的构网型VSG变流器的内电势、输出端电压和输出电流之间关系的频域主电路核心方程为：

（14）

三相VSG系统采用空间矢量脉宽调制算法，不考虑调制过程以及开关过程，则可将VSG三相调制波视为桥臂电势[12]，认为理想调制，即调制比等效为1。

对构网型VSG变流器降维SISO等效序阻抗的计算，需要综合考虑主电路系统与控制系统的约束方程，下面将通过对各个控制环节进行建模，最终推导出VSG的SISO等效序阻抗解析模型。 

3.2.2 VSG有功外环的小干扰频域表达式推导

考虑相角小信号扰动后θp=θ1+∆θ，其中θ1为基频相角，∆θ为相角扰动分量，对Park正变换矩阵进行线性化处理可得：

​​

（15）

式（15）中，Tabc/dq（θ1）为基频相角变换模块，Tabc/dq（∆θ）为扰动相角变换模块。求解∆θ是关键。经过基频相角变换模块的dq轴并网电压、并网电流分别如下：

​​ （16）

​​ （17）

将公式（16）、（17）各分量（直流量、正/负扰动量）代入小信号线性化展开后的公式（11），忽略高阶非线性耦合（无穷小之积为零），考虑频域变量幅值乘以2为时域变量的幅值（欧拉变换），则可得构网型VSG变流器的有功功率、无功功率频域表达式分别为：

​​ （18）

​​ （19）

上式中，上标“*”表示复数的共轭量；​​ ；。

根据有功控制环，可获得构网型VSG变流器内电势相位θ，考虑相角扰动Δθ，即θ=θ1+Δθ。令M(s)=1/[s(Dp+Js)]，将式（14）、式（15）代入式（2）中θv的计算表达式，可得基频相角θ1和相角小扰动Δθ的频域表达式分别如式（16）、式（17）所示：

（20）

其中，​​。

接下来，推导Park变换矩阵中坐标变换基准角，由于Δθ是由有功功率小扰动信号引起的，考虑相角扰动Δθ，即θ=θ1+Δθ。结合三角变换，可得：

（21）

将式（20）代入式（21），结合频域卷积定理，并忽略高频非线性耦合（无穷小之积为零），则cosθ、sinθ的频域表达式为：

​​ （22）

（23）

3.2.3 VSG无功外环的小干扰频域表达式推导

文献[2]忽略VSG无功环路的影响，阻抗建模过程中认为VSG内电势幅值为常量，即Em(s)=Em0（Em0为基频电压）。无功环路均会对VSG端口动态特性产生较大影响，为建立准确的构网型VSG变流器阻抗模型，有必要考虑无功环路的影响[6-7,9-10]。本文考虑VSG无功环路对扰动信号的作用，将式（3）变换可得VSG内电动势幅值Em的频域表达式为：

​​（24）

对式（24）进行小信号线性化处理，则VSG内电动势幅值Em的各频次分量表达式为：

​​ （25）

其中，​​ 。

3.2.4 电压电流双闭环输出调制函数的小干扰频域表达式推导

根据图2中电压电流双闭环控制框图的电压外环部分，可知电压外环dq轴参考值频域表达式如下：

​​ （26）

采用考虑完整相角（θp=θ1+∆θ）的Park变换矩阵（式（15））对并网电压vgabc进行坐标变换，即Park变换矩阵式（15）中先左乘基频相角变换矩阵，可得vd1、vq1，再左乘扰动相角变换矩阵，可得最终的并网电压dq轴分量vd、vq。并网电压dq轴分量频域表达式如下：（需要说明的是，sinΔθ约等于Δθ；cosΔθ约等于1）

​​（24）

将式（16）、（20）代入式（24），忽略二次扰动项，可得：（标红部分为扰动相角引入的区别于式（16）的增项）

​​ ​​​​​​（25）

​​ （26）

同理，可得并网电流dq轴分量Id、Iq：（区别于式（17），标红部分为扰动相角引入的增项）

​​ （27）

​​ （28）

并网电压dq轴分量经过电压外环产生电流内环输入参考值Id_ref，电压外环的频域表达式如下（考虑dq轴频率偏移）：

​​ （29）

式（29）经过小信号线性化（Laplace变换）处理（Vd_ref和Vq_ref均为常量，∆Vd_ref、∆Vq_ref等于0），可得电压外环输入与输出之间的小信号频域表达式为：

​​ （30）

其中，Gv、Gi分别为电压外环控制P环节、电流内环控制PI环节的传递函数，即

​​ （31）

式中，kpv分别为电压外环的比例增益；kpi、kii分别为电压内环的比例、积分增益。

式（30）经过小信号线性化处理，可得电流内环输入与输出之间的正序小信号频域表达式为：

​​ （32）

（33）

其中，Kpwm为调制系数，Kpwm=1/Vdc。

3.2.5 构网型VSG变流器端口二维耦合序阻抗求解

求得调制波的dq分量后，根据Park反变换可以得到abc坐标系下调制波分量。VSG的a相桥臂电压和调制度以及直流电压存在如下关系：

（34）

考虑相角小信号扰动后θp=θ1+∆θ，其中θ1为基频相角，∆θ为相角扰动分量，对Park反变换矩阵进行线性化处理可得：

​​

​​

​​（35）

将控制系统输出的dq轴参考电压（正序/负序）经过式（42）的Park反变换后，可获得三相abc坐标系下的参考电压Mabc：

​​

​​​​（43）

对式（43）进行分解计算，经过扰动相角反变换矩阵后的dq轴参考电压Md1、Mq1如下（无穷小之积为0）：

​​

（44）

最终可得到A相调制电压ma的表达式为：

（45）

以正序为例，对式（44）整理可得（小信号之积为0）：

（46）

将公式（46）代入（45），可得：

（47）

结合式（34），可得A相桥臂内电势的表达式为：

（48）

其中，fp扰动频次信号的系数矩阵为：

（49）

fp-2f1耦合频次信号的系数矩阵为：

（50）

联立公式（5）、（13）、（14）、（48），可求解出考虑频率耦合效应的构网型VSG二维耦合序阻抗矩阵为：

（51）

（52）

根据式（52）可知，构网型VSG并网系统是一个单输入双输出系统，存在频率耦合效应，即向系统中注入某一频率扰动电压会产生相同频率的电流响应和耦合频率的电流响应。与前文分析一致。

3.2.6 构网型VSG变流器端口降维SISO等效序阻抗求解

由上述计算可得到构网型VSG并网系统的二维耦合阻抗模型，进一步根据图8及公式（6），通过电网阻抗Zg消除fp-2f1耦合频率的变量，考虑耦合项的影响并等效计算到输出阻抗中，使单输入双输出系统简化为SISO系统，便于阻抗求解及系统稳定性分析，可求解得到保留频率耦合效应的正负序降维SISO阻抗（Zvsg_equi_p、Zvsg_equi_n）模型。

4、构网型VSG变流器降维SISO等效序阻抗验证及对比

本文理论层面的推导到此结束。为了验证所建立构网型VSG变流器降维SISO等效序阻抗模型在宽频段内的正确性，提供一组系统参数及构网型VSG变流器序阻抗扫频实现案例。构网型VSG变流器的主要电气参数如表1所示。基于Matlab/Simulink平台搭建构网型VSG变流器时域仿真模型，将构网型VSG变流器序阻抗理论计算结果与时域阻抗扫频仿真结果进行对比。扫频原理图如图9所示，扫频对比结果如图10所示。

构网型VSG变流器阻抗建模及扫频的更多实现细节不便于全部展开，欢迎留言讨论，各位如果有需要获取本文章中涉及的代码和模型，可联系QQ：2293540475。希望对大家有所帮助。

4.1 阻抗扫频测量思路和流程

扫频思路：推导建立跟网型变流器的序阻抗模型后，利用Matlab代码实现理论阻抗建模，基于Matlab/Simulink平台或搭建仿真模型并利用谐波线性化原理进行扫频，将理论阻抗Bode图与扫频阻抗特性进行对比，验证宽频范围内阻抗模型的正确性。阻抗扫频原理示意图如图9所示。

​​​

图9  阻抗扫频原理示意图

阻抗建模及扫频对比详细流程如下：

①  根据第5章推导的构网型VSG变流器序阻抗解析表达式，利用Matlab代码建立s变量下序阻抗模型，并基于程序扫频代入具体频率序列求解对应的序阻抗值，分解为幅值和相位，绘制bode图描述阻抗特性。

②  基于Matlab/Simulink平台搭建构网型VSG交流并网仿真模型，并调整运行正确。

③  设置扫频用的扰动频率序列，仿真模型运行至稳态后，采用串联电压源的方式向VSC侧分别逐一注入扰动频率处的正序、负序电压小扰动。

④  待注入扰动达到新稳态后，获取并网PCC点处的三相电压、电流信号进行FFT分析，得到扰动频率下三相电压、电流信号的幅值和相位。

⑤  重复③ ④步骤，将电压扰动和扰动频率处电流响应相除（参考本文式（10））求解得扫频阻抗特性。

⑥  将理论阻抗Bode图与扫频阻抗特性进行对比，验证宽频范围内阻抗模型的正确性。

4.2 算例模型及扫频对比

图10为考虑频率耦合的构网型VSG变流器降维SISO等效序阻抗扫频对比图，图11为考虑频率耦合降维前后的构网型VSG变流器序阻抗对比及扫频结果。从图10的构网型VSG变流器降维SISO等效序阻抗扫频对比图中可以看出，本文所建立的考虑频率耦合效应的构网型VSG变流器降维SISO等效序阻抗模型在全频段内与扫频测量结果高度吻合，说明了本文所建立的构网型VSG变流器降维SISO序阻抗模型的精确性。

从图10可看出，构网型VSG变流器降维SISO阻抗的正序特性在1Hz~28Hz的次同步频段呈现为“正电阻+电容”特性，在51Hz~100Hz的超同步频段以及100Hz~1000Hz的中高频段下均呈现为“正电阻+电感”特性，在29Hz~50Hz的次同步频段存在负阻容特性，原因是构网型VSG变流器VSG功率外环及控制结构的频率耦合效应引起的[9-10]。负序阻抗特性在1Hz~100Hz的次/超同步频段下呈现为“正电阻+电容”特性，即在弱电网工况下不易构成二阶负阻尼振荡电路，因此大大降低了系统次/超同步振荡风险。可见，相比于跟网型变流器，构网型VSG变流器更适应于弱网场景运行。一方面对现有运行于弱电网地区的跟网型场站，按一定容量配比并入构网型VSG变流器可有效降低系统振荡风险，另一方面，对即将投产的新建新能源场站，实现新能源的友好并网、稳定运行。文献[4]指出，构网型VSG变流器电路特性主要取决于无功控制环节和电压外环，受有功控制环节影响较小，感兴趣可自行验证。此外，构网型VSG变流器与跟网型变流器并联运行时，构网型VSG变流器的“正电阻+电感”特性可改善跟网型变流器的“负电阻+电容”特性，使得多机/多变流器并联系统呈现“正电阻+电感”的正阻尼特性，从根源上避免形成振荡电路的可能，即构网型VSG变流器具有改善跟网型变流器弱电网下次/超同步振荡稳定性的能力。

从图11可看出，考虑频率耦合的构网型VSG变流器降维SISO阻抗模型相比于典型的正负序阻抗模型，阻抗模型精度更高。频率耦合效应对输出阻抗影响主要体现在基频50Hz附近频段，频率耦合效应使得正序阻抗在50Hz附近阻抗幅值大幅度降低，增加了VSG正序输出阻抗与电网阻抗发生交互的可能，此外正序阻抗相频特性曲线在29Hz~50Hz的次同步频段急剧降低，负阻容特性更明显，对于强电网工况，可能与电网交互导致相位裕度小于零，从而存在系统振荡失稳风险，因此需要采用虚拟阻抗抑制构网型并网系统次同步频段的负阻尼特性，提升宽频范围内的并网稳定性。从阻抗扫频的角度观察，忽略频率耦合效应时，50Hz附近阻抗测量点与理论曲线存在偏差，而采用本文方法建立降维SISO等效序阻抗模型可以与扫频点较好地吻合，表明考虑频率耦合效应的阻抗模型精度更高，可模拟实际的动态特性。值得注意的是，文献[4指出，阻抗矩阵的主对角元素/自阻抗元素在小干扰稳定性分析中起主导作用，当研究系统为三相对称、电流环对称系统，可不考虑频率耦合对VSG序阻抗模型的影响。若专门研究频率耦合效应，则更适合于采用本文所建立的降维SISO等效序阻抗模型。

构网型VSG变流器电气参数

参数	数值
额定有功功率Pref/kW	7
额定无功功率Qref/kVar	0.3
直流电压Vdc/V	800
电网线电压V1/V	380
额定频率f1/Hz	50
逆变器侧滤波电感Lf/mH	3
滤波电容Cf/μF	10
滤波电容寄生电阻Rf/mΩ	5
电网电感Lg/mH	10
惯量系数J/(kg·m2)	0.058
有功阻尼系数Dp	5
无功阻尼系数Dq	320
无功电压系数K	6.5
电压外环比例系数kpv	1.2
电流内环比例系数kpi	6
电流内环积分系数kii	0.1

​​（a）正序

​​

（b）负序

图10 构网型VSG变流器降维SISO等效序阻抗扫频对比结果

 

​​（a）正序

​​

（b）负序

图11 考虑频率耦合降维前后的构网型VSG变流器序阻抗对比及扫频结果

除了仿真扫频的方法外，可基于控制硬件在环实时仿真实现阻抗扫频测量，也是一种分析阻抗特性的有效研究与实验手段，其阻抗测量结果受仿真平台性能参数的影响。这部分内容本文不展开写了，有感兴趣的可学习文献[13]-[14]等。

5、小干扰稳定性专栏出版声明

出版声明：小干扰稳定性专栏已发布十余篇文章，后续将继续给大家呈现一系列小干扰稳定性相关的文章，包含但不限于考虑附加阻尼虚拟阻抗的构网型新能源并网系统SISO等效阻抗建模及振荡抑制分析、跟网型并网系统SISO等效阻抗建模及振荡抑制分析、新能源/多机/多变流器型并网系统控制交互作用特性及机理分析、大规模新能源并网系统等值阻抗建模及动态特性分析、基于谐波状态空间/多谐波线性化的MMC交直流侧序阻抗建模及稳定性分析、MMC高频简化等效阻抗建模及稳定性分析等，有助于帮助初学者入门、入门者创新、研究人员解决问题、突破瓶颈。期间有任何疑问或需要的可随时联系。

共同进步！感谢支持！敬请期待！

6、文章版权声明

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

参考文献

[1]刘朋印,谢小荣,李原,等.构网型控制改善跟网型变流器次/超同步振荡稳定性的机理和特性分析[J].电网技术,2024,48(03):990-997.

[2] 伍文华.新能源发电接入弱电网的宽频带振荡机理及抑制方法研究[D].湖南大学,2019.

[3] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J/OL].中国电机工程学报,1-15[2024-07-04].http://kns.cnki.net/kcms/detail/11.2107.TM.20240124.1816.011.html.

[4]刘朋印,谢小荣,李原,等.构网型控制改善跟网型变流器次/超同步振荡稳定性的机理和特性分析[J].电网技术,2024,48(03):990-997.

[5] 胡宇飞,田震,查晓明,等.构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J].电力系统自动化,2022,46(24):121-131.

[6] K. Shi, Y. Wang, Y. Sun, P. Xu and F. Gao, "Frequency-Coupled Impedance Modeling of Virtual Synchronous Generators," in IEEE Transactions on Power Systems, vol. 36, no. 4, pp. 3692-3700, July 2021.

[7] Yifeng Liu, Xiaoping Zhou, Haoqi Yu, et al. Sequence Impedance Modeling and Stability Assessment for Load Converters in Weak Grids[J].IEEE Transactions on Ind. Electron., vol. 68, no. 5,  pp. 4056–4067, May 2021.

[8] 徐韵扬.振荡频率耦合下风电机组的阻抗建模与并网稳定性分析[D].浙江大学,2021.

[9] 赵韩广.虚拟同步发电机的序阻抗建模分析与稳定控制[D].合肥工业大学,2021.

[10] 郭志博.基于虚拟同步发电机的逆变器序阻抗建模与并网稳定性研究[D].华北电力大学,2024.

[11] 宗皓翔,张琛,吕敬,等.MMC多入多出阻抗及其在不对称小扰动稳定分析中的应用[J].中国电机工程学报, 2022, 42(15):15.

[12] 胡宇飞,田震,查晓明,等.构网型与跟网型变流器主导孤岛微网阻抗稳定性分析及提升策略[J].电力系统自动化,2022,46(24):121-131.

[13] 李光辉，王伟胜，刘纯，何国庆，叶俭，孙建．基于控制硬件在环的风电机组阻抗测量及影响因素分析[J]．电网技术，2019，43(5)：1624-1631．

[14] 马宁宁，杜维柱，刘朋印，李蕴红，刘威，谢小荣．基于控制硬件在环测试的风电次/超同步振荡风险评估[J]．中国电机工程学报，2022，42(15)：5497-5505．