深度学习03 人工神经网络ANN
什么是神经网络
人工神经网络( Artificial Neural Network, 简写为ANN)也简称为神经网络(NN),是一种模仿生物神经网络结构和功能的计算模型,人脑可以看做是一个生物神经网络,由众多的神经元连接而成.各个神经元传递复杂的电信号,树突接收到输入信号,然后对信号进行处理,通过轴突输出信号.

当电信号通过树突进入到细胞核时,会逐渐聚集电荷。达到一定的电位后,细胞就会被激活,通过轴突发出电信号。
构建人工神经网络
神经网络由多个神经元组成,构建神经网络就是构建神经元.基础神经元如下

这个过程就像,来源不同树突(树突都会有不同的权重)的信息, 进行的加权计算, 输入到细胞中做加和,再通过激活函数输出细胞值。
然后使用多个神经元构成神经网络,相邻层的神经元互相连接

神经网络中信息只向一个方向移动,即从输入节点向前移动,通过隐藏节点,再向输出节点移动。其中的基本部分是:
- 输入层(Input Layer): 即输入x的那一层(如图像、文本、声音等)。每个输入特征对应一个神经元。输入层将数据传递给下一层的神经元。
- 输出层(Output Layer): 即输出y的那一层。输出层的神经元根据网络的任务(回归、分类等)生成最终的预测结果。
- 隐藏层(Hidden Layers): 输入层和输出层之间都是隐藏层,神经网络的“深度”通常由隐藏层的数量决定。
隐藏层的神经元通过加权和激活函数处理输入,并将结果传递到下一层。 特点是:
- 同一层的神经元之间没有连接
- 第 N 层的每个神经元和第 N-1层 的所有神经元相连(这就是full connected的含义),这就是全连接神经网络
- 全连接神经网络接收的样本数据是二维的,数据在每一层之间需要以二维的形式传递
- 第N-1层神经元的输出就是第N层神经元的输入 每个连接都有一个权重值(w系数和b系数)
神经网络内部状态值和激活值

内部状态值是是神经元对输入信号的加权求和结果,加上偏置项后的线性组合。
wi为内部状态值梯度(权重矩阵与偏置可以初始化)

激活值(通常记为 a)是内部状态值通过激活函数 f(⋅) 非线性变换后的输出,如sigmoid,tanh,relu,softmax即

总的来说,神经网络是一种模仿生物神经网络结构和功能的计算模型,由输入层,输出层,和隐藏层构成,每一层都由神经元构成.
神经元包含内部状态值梯度w,偏置值b,激活函数f(x),通过对外部输入进行加权计算得到内部状态值z,将z输入激活函数进行非线性变换得到激活值传给下一个神经元或者输出.
激活函数
激活函数用于对每层的输出数据进行变换,进而为整个网络注入了非线性因素.此时,神经网络就可以你和各种曲线.
- 如果没有引入非线性因素,神经网络等价于一个线性模型
- 通过给网络输出增加激活函数, 实现引入非线性因素, 使得网络模型可以逼近任意函数, 提升网络对复杂问题的拟合能力.
如果不使用激活函数,整个网络虽然看起来复杂,其本质还相当于一种线性模型,如下公式所示:

常见激活函数及特点

激活函数作用:向神经网络中添加非线性因素
激活函数选择方法:relu能且仅能用于隐藏层,输出层二分类常用sigmoid,多分类常用softmax
激活函数参数初始化
参数初始化在神经网络训练中扮演着至关重要的角色,它直接影响模型的收敛速度、训练稳定性以及最终性能。
核心作用:
- 打破对称性
若所有参数初始化为相同值(如零初始化),神经元在反向传播时会接收到相同的梯度更新,导致网络无法学习差异化特征。随机初始化(如正态分布或均匀分布)通过赋予参数不同的初始值,确保神经元学习不同的特征.
- 控制梯度传播稳定性
初始化值过大可能导致梯度爆炸(权重更新失控),过小则导致梯度消失(浅层参数无法更新)。例如,Xavier和Hekaiming初始化通过调整权重范围,使各层输出的方差保持一致,从而稳定梯度传播
- 加速模型收敛
合理的初始化(如Xavier或He初始化)能使网络在训练初期处于更优的起始状态,减少收敛所需的迭代次数。
- 适配激活函数特性
不同激活函数对初始化范围的要求不同,如:
Sigmoid/Tanh:适合Xavier初始化,因其需要对称的输入分布
ReLU:He初始化通过调整方差适应ReLU的“单侧抑制”特性
常见初始化方式及对比

激活函数初始化选择
模拟搭建神经网络 如图

+1为偏置,及z=wx+b的b
是偏置节点的可视化表示,它通过引入可学习的偏置权重,帮助神经网络摆脱输入空间的限制,显著提升模型的表达能力,它允许神经元的激活函数在输入全为0时也能产生非零输出,增强模型的灵活性。如果没有偏置,许多简单的分类问题(如异或问题)将无法被正确拟合。
具体步骤如下
# 导包
from torch.nn import Module, Linear
import torch
# 提前安装torchsummary,然后导入summary查看模型参数
# pip install torchsummary
from torchsummary import summary# TODO 1.自定义模型类继承Module类
class My_Model(Module):# TODO 2.重写init魔法方法和forward前向传播方法def __init__(self, *args, **kwargs):# 1.调用父类的init初始化方法super().__init__(*args, **kwargs)# TODO 定义神经网络结构self.linear1 = Linear(3, 3)self.linear2 = Linear(3, 2)self.out = Linear(2, 2)# 3.参数初始化(生成权重矩阵和偏置矩阵)# 隐藏层初始化权重矩阵torch.nn.init.xavier_normal_(self.linear1.weight)torch.nn.init.kaiming_normal_(self.linear2.weight)# 隐藏层初始化偏置矩阵torch.nn.init.zeros_(self.linear1.bias)torch.nn.init.zeros_(self.linear2.bias)def forward(self, x):# TODO 前向传播计算(每层都是加权求和+激活函数)x = torch.sigmoid(self.linear1(x))x = torch.relu(self.linear2(x))# 此处-1代表最后一维, 也就是按照每个样本概率和为1.x = torch.softmax(self.out(x), dim=-1)# 返回结果return x# TODO 3.创建模型对象并使用模型对象
# 创建模型对象
model = My_Model() # 自动调用init魔法方法
# 准备数据集(正态分布数据)
torch.manual_seed(66)
data = torch.randn(5, 3) # 5个样本,3个特征
print(data)
# 把数据传入模型对象
output = model(data) # 自动调用forward方法
print(output)
print('============================================================')
# TODO summary()查看模型参数
summary(model, (3,), batch_size=5) # 第1层:12,第2层:8,第3层:6
print('============================================================')
# TODO 遍历查看模型名字和对应参数
for name, param in model.named_parameters():print(f'参数名称: {name}, 参数值: {param}')print('---------------------------------')
损失函数
在机器学习中就已经引入了损失函数的概念,在此回顾一遍
损失函数是衡量模型参数质量的函数,又叫代价函数,误差函数等等,根据损失函数计算损失值,结合反向传播算法以及梯度下降算法实现参数的更新.(前向传播和方向传播在后续优化方法中会提到)
损失函数分为两大类:
- 分类损失函数
- 多分类交叉熵损失函数:nn.CrossEntropyLoss(reduction='mean') [实现softmax激活值计算+损失计算]
- 二分类交叉熵损失函数:nn.BCELoss(reduction='mean')
- 回归损失函数:
- MAE平均绝对误差损失函数:nn.MSEloss(),计算平均绝对误差
- MSE均方误差损失函数:nn.MSEloss(),计算均方误差
- Huber Loss损失函数:指定a值,小于a使用MSE,大于a使用MAE使得损失值更平滑
- Smooth L1损失函数:a=1的Huber Loss损失函数
网络模型优化方法 学习率 梯度 正则化
众所周知,损失函数是衡量模型参数好坏的标准,而模型参数是通过梯度下降来进行更新的,也就是说,要优化模型,就是优化梯度下降算法,梯度下降公式为:

不难看出:仅有的两个变量为学习率和梯度,梯度通常指损失函数关于模型参数的导数,因此优化方法需要从这俩入手
梯度下降法三大概念
epoch:训练次数/轮次
batch_size: 每次迭代需要的样本数
iteration:每次训练需要迭代多少次:样本数/batch_size[+1, 不能整除需要加1]
正向传播与反向传播
正向传播(Forward Propagation)是神经网络中数据从输入层逐层传递到输出层的过程。每一层的神经元接收前一层输出的加权求和结果,并通过激活函数生成该层的输出,最终得到网络的预测结果。

反向传播(Backpropagation)是训练神经网络的核心算法,用于计算损失函数对网络参数的梯度。通过链式法则,梯度从输出层反向传播到输入层,指导参数更新以最小化损失。

反向梯度计算:

参数更新:梯度= 损失值对网格参数w求导,显而易见,梯度是逐级向上逐渐求出的,最终每一个梯度都会被更新,需要注意的是,梯度的计算路径即反向传播路径不止一条.

梯度下降的两种优化方式:梯度角度和学习率角度
指数加权平均思想:根据历史指数加权值与当天值加权计算得出当前指数加权平均值
当处于第一天时,new历史加权指数平均值==第一天的值
当处于第二天时,new历史加权指数平均值=b*历史加权平均值=(1-b)*第二天值
当处于第三天时,new历史加权指数平均值=b*历史加权平均值=(1-b)*第三天值
....
此思想是优化方法的核心思路


在梯度角度的优化方法
BGD 每次迭代时使用全部训练数据计算损失函数的梯度,并更新模型参数 准但是慢
SGD 每次迭代仅使用一个样本或一小批样本来计算梯度 快但是不准
MBGD 选几个梯度更新 不慢较准
momentum动量法 当前梯度是指数移动加权平均梯度
引入了指数加权平均思想
梯度 == 当前梯度*系数+历史加权平均梯度*(1-系数)
St=(1-β)*Gt + β*St-1
在学习率角度优化的方法
- 自动调整
adagrad:自动调整学习率,初始大,后期小
新学习率=原始学习率/历史梯度平方
RMSprop:新学习率=旧学习率/历史梯度加权平方
Adam:是RMSprop学习率更新+momentun梯度更新一起使用
- 手动调整
等间隔:lr = lr * gamma
scheduer = optim.lr_scheduler.StepLR(optimizer=optimizer, step_size=50, gamma=0.5)
指定间隔:lr = lr * gamma
optim.lr_scheduler.MultiStepLR(optimizer=optimizer, milestones=[50, 100, 160], gamma=0.5, last_epoch=-1)
指数衰减:lr = lr*gamma**epoch
optim.lr_scheduler.ExponentialLR(optimizer=optimizer, gamma=0.9)

优化器的选择
深度学习默认选择adam:适合大多数深度学习任务
SGD+momentum:更好的泛化性能,如cv任务
adagrad或者RMS适合用于稀疏数据或者特定任务
正则化
防止机器学习模型过拟合的技术,通过在损失函数中添加额外的惩罚项,限制模型参数的大小或复杂度。其核心目标是提高模型在未知数据上的泛化能力。
范数正则化
L1正则化(Lasso回归)
L2正则化(岭回归)

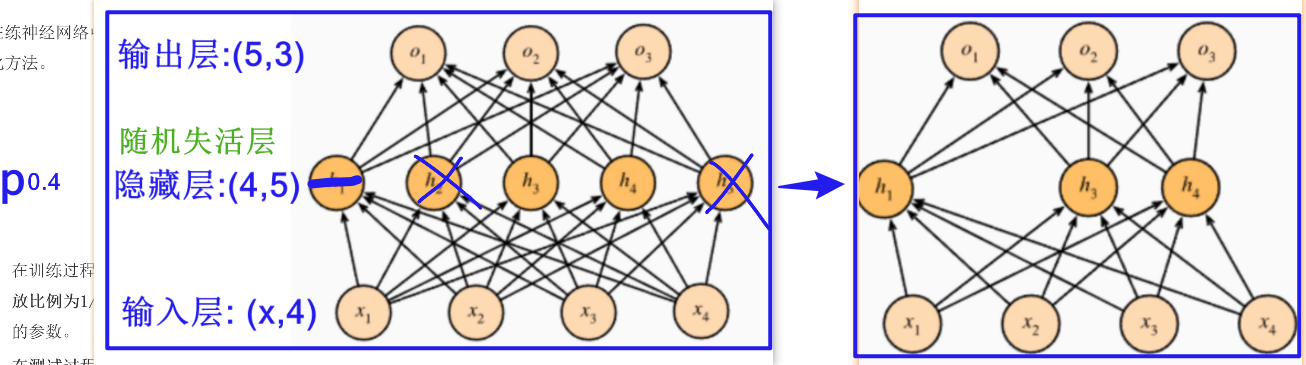
随机失活正则化
dropout层
以指定p概率让神经元随机失活
批量归一正则化
实现原理:对线性结果进行标准化处理, 根据每批样本的均值和标准差计算标准化的值
注意点
- 在激活层前使用(卷积层后/线性层后)
- 多数在计算机视觉领域使用
- 可以引入γ和β可学习参数, 不同层的样本分布在不同范围内(不同层使用的激活函数不同); 可以补回标准化丢失的信号

