OCCT基础类库介绍：Modeling Data - 2D Geometry 3D Geometry Topology

2D Geometry

Geom2d package defines geometric objects in 2dspace. All geometric entities are STEP processed. The objects are handled by reference.

二维几何

Geom2d 包定义二维空间中的几何对象，所有几何实体均经过 STEP 处理。对象通过引用方式处理。

In particular, Geom2d package provides classes for:

• description of points, vectors and curves,
• their positioning in the plane using coordinate systems,
• their geometric transformation, by applying translations, rotations, symmetries, scaling transformations and combinations thereof.

具体而言，Geom2d 包提供以下类：

• 点、向量和曲线的描述，
• 通过坐标系在平面中定位这些对象，
• 应用平移、旋转、对称、缩放变换及其组合进行几何变换。

The following objects are available:

• point,
• Cartesian point,
• vector,
• direction,
• vector with magnitude,
• axis,
• curve,
• line,
• conic: circle, ellipse, hyperbola, parabola,
• rounded curve: trimmed curve, NURBS curve, Bezier curve,
• offset curve.

可用对象如下：

• 点，
• 笛卡尔点，
• 向量，
• 方向，
• 带模向量，
• 轴，
• 曲线，
• 直线，
• 圆锥曲线：圆、椭圆、双曲线、抛物线，
• 圆角曲线：修剪曲线、NURBS 曲线、贝塞尔曲线，
• 偏移曲线。

Before creating a geometric object, it is necessary to decide how the object is handled. The objects provided by Geom2d package are handled by reference rather than by value. Copying an instance copies the handle, not the object, so that a change to one instance is reflected in each occurrence of it. If a set of object instances is needed rather than a single object instance, TColGeom2d package can be used. This package provides standard and frequently used instantiations of one-dimensional arrays and sequences for curves from Geom2d package. All objects are available in two versions:

• handled by reference and
• handled by value.

创建几何对象前，需确定对象的处理方式。Geom2d 包提供的对象通过引用而非值处理。复制实例时复制的是句柄而非对象，因此一个实例的更改会反映在所有引用该实例的地方。如果需要对象实例集而非单个实例，可使用 TColGeom2d 包，该包为 Geom2d 包中的曲线提供一维数组和序列的标准常用实例化。所有对象均有两种版本：

• 引用处理
• 值处理

The key characteristic of Geom2d curves is that they are parameterized. Each class provides functions to work with the parametric equation of the curve, and, in particular, to compute the point of parameter u on a curve and the derivative vectors of order 1, 2…, N at this point.

Geom2d 曲线的关键特征是参数化。每个类都提供处理曲线参数方程的函数，尤其是计算曲线上参数 u 处的点以及该点处 1、2…N 阶导向量的函数。

As a consequence of the parameterization, a Geom2d curve is naturally oriented.

Parameterization and orientation differentiate elementary Geom2dcurves from their equivalent as provided by gp package. Geom2d package provides conversion functions to transform a Geom2d object into a gp object, and vice-versa, when this is possible.

由于参数化，Geom2d 曲线具有自然方向。

参数化和方向使基本 Geom2d 曲线与其在 gp 包中的等效曲线区分开来。Geom2d 包提供转换函数，在可能的情况下将 Geom2d 对象转换为 gp 对象，反之亦然。

Moreover, Geom2d package provides more complex curves, including Bezier curves, BSpline curves, trimmed curves and offset curves.

此外，Geom2d 包还提供更复杂的曲线，包括贝塞尔曲线、B 样条曲线、修剪曲线和偏移曲线。

Geom2d objects are organized according to an inheritance structure over several levels.

Thus, an ellipse (specific class Geom2d_Ellipse) is also a conical curve and inherits from the abstract class Geom2d_Conic, while a Bezier curve (concrete class Geom2d_BezierCurve) is also a bounded curve and inherits from the abstract class Geom2d_BoundedCurve; both these examples are also curves (abstract class Geom2d_Curve). Curves, points and vectors inherit from the abstract class Geom2d_Geometry, which describes the properties common to any geometric object from the Geom2d package.

Geom2d 对象按多层继承结构组织。

因此，椭圆（具体类 Geom2d_Ellipse）也是圆锥曲线，继承自抽象类 Geom2d_Conic；而贝塞尔曲线（具体类 Geom2d_BezierCurve）也是有界曲线，继承自抽象类 Geom2d_BoundedCurve；这两个示例也都是曲线（抽象类 Geom2d_Curve）。曲线、点和向量继承自抽象类 Geom2d_Geometry，该类描述 Geom2d 包中任何几何对象的共同属性。

This inheritance structure is open and it is possible to describe new objects, which inherit from those provided in the Geom2d package, provided that they respect the behavior of the classes from which they are to inherit.

此继承结构是开放的，只要遵循要继承的类的行为，就可以描述继承自 Geom2d 包中提供的对象的新对象。

Finally, Geom2d objects can be shared within more complex data structures. This is why they are used within topological data structures, for example.

最后，Geom2d 对象可以在更复杂的数据结构中共享，例如，这就是它们在拓扑数据结构中使用的原因。

Geom2dpackage uses the services of the gp package to:

• implement elementary algebraic calculus and basic analytic geometry,
• describe geometric transformations which can be applied to Geom2d objects,
• describe the elementary data structures of Geom2d objects.

Geom2d 包使用 gp 包的服务来：

• 实现基本代数计算和基本解析几何，
• 描述可应用于 Geom2d 对象的几何变换，
• 描述 Geom2d 对象的基本数据结构。

However, the Geom2d package essentially provides data structures and not algorithms. You can refer to the GCE2d package to find more evolved construction algorithms for Geom2d objects.

但是，Geom2d 包本质上提供数据结构而非算法。可参考 GCE2d 包找到更高级的 Geom2d 对象构造算法。

3D Geometry

The Geom package defines geometric objects in 3d space and contains all basic geometric transformations, such as identity, rotation, translation, mirroring, scale transformations, combinations of transformations, etc. as well as special functions depending on the reference definition of the geometric object (e.g. addition of a control point on a B-Spline curve,modification of a curve, etc.). All geometrical entities are STEP processed.

三维几何

Geom 包定义三维空间中的几何对象，包含所有基本几何变换（如恒等、旋转、平移、镜像、缩放变换、变换组合等），以及取决于几何对象参考定义的特殊函数（如 B 样条曲线上添加控制点、曲线修改等）。所有几何实体均经过 STEP 处理。

In particular, it provides classes for:

• description of points, vectors, curves and surfaces,
• their positioning in 3D space using axis or coordinate systems, and
• their geometric transformation, by applying translations, rotations, symmetries, scaling transformations and combinations thereof.

具体而言，它提供以下类：

• 点、向量、曲线和曲面的描述，
• 通过轴或坐标系在三维空间中定位它们，
• 应用平移、旋转、对称、缩放变换及其组合进行几何变换。

The following objects are available:

• Point
• Cartesian point
• Vector
• Direction
• Vector with magnitude
• Axis
• Curve
• Line
• Conic: circle, ellipse, hyperbola, parabola
• Offset curve
• Elementary surface: plane, cylinder, cone, sphere, torus
• Bounded curve: trimmed curve, NURBS curve, Bezier curve
• Bounded surface: rectangular trimmed surface, NURBS surface,Bezier surface
• Swept surface: surface of linear extrusion, surface of revolution
• Offset surface.

可用对象如下：

• 点
• 笛卡尔点
• 向量
• 方向
• 带模向量
• 轴
• 曲线
• 直线
• 圆锥曲线：圆、椭圆、双曲线、抛物线
• 偏移曲线
• 基本曲面：平面、圆柱、圆锥、球体、圆环
• 有界曲线：修剪曲线、NURBS 曲线、贝塞尔曲线
• 有界曲面：矩形修剪曲面、NURBS 曲面、贝塞尔曲面
• 扫掠曲面：线性拉伸曲面、旋转曲面
• 偏移曲面

The key characteristic of Geom curves and surfaces is that they are parameterized. Each class provides functions to work with the parametric equation of the curve or surface, and, in particular, to compute:

• the point of parameter u on a curve, or
• the point of parameters (u, v) on a surface. together with the derivative vectors of order 1, 2, … N at this point.

Geom 曲线和曲面的关键特征是参数化。每个类都提供处理曲线或曲面参数方程的函数，尤其是计算：

• 曲线上参数 u 处的点，或
• 曲面上参数 (u, v) 处的点，以及该点处 1、2…N 阶导向量。

As a consequence of this parameterization, a Geom curve or surface is naturally oriented.

Parameterization and orientation differentiate elementary Geom curves and surfaces from the classes of the same (or similar) names found in gp package. Geom package also provides conversion functions to transform a Geom object into a gp object, and vice-versa, when such transformation is possible.

由于这种参数化，Geom 曲线或曲面具有自然方向。

参数化和方向使基本 Geom 曲线和曲面与 gp 包中同名（或类似名）的类区分开来。Geom 包还提供转换函数，在可能的情况下将 Geom 对象转换为 gp 对象，反之亦然。

Moreover, Geom package provides more complex curves and surfaces, including:

• Bezier and BSpline curves and surfaces,
• swept surfaces, for example surfaces of revolution and surfaces of linear extrusion,
• trimmed curves and surfaces, and
• offset curves and surfaces.

此外，Geom 包还提供更复杂的曲线和曲面，包括：

• 贝塞尔和 B 样条曲线和曲面，
• 扫掠曲面，例如旋转曲面和线性拉伸曲面，
• 修剪曲线和曲面，以及
• 偏移曲线和曲面。

Geom objects are organized according to an inheritance structure over several levels. Thus, a sphere (concrete class Geom_SphericalSurface) is also an elementary surface and inherits from the abstract class Geom_ElementarySurface, while a Bezier surface (concrete class Geom_BezierSurface) is also a bounded surface and inherits from the abstract class Geom_BoundedSurface; both these examples are also surfaces (abstract class Geom_Surface). Curves, points and vectors inherit from the abstract class Geom_Geometry, which describes the properties common to any geometric object from the Geom package.

Geom 对象按多层继承结构组织。因此，球体（具体类 Geom_SphericalSurface）也是基本曲面，继承自抽象类 Geom_ElementarySurface；而贝塞尔曲面（具体类 Geom_BezierSurface）也是有界曲面，继承自抽象类 Geom_BoundedSurface；这两个示例也都是曲面（抽象类 Geom_Surface）。曲线、点和向量继承自抽象类 Geom_Geometry，该类描述 Geom 包中任何几何对象的共同属性。

This inheritance structure is open and it is possible to describe new objects, which inherit from those provided in the Geom package, on the condition that they respect the behavior of the classes from which they are to inherit.

此继承结构是开放的，只要遵循要继承的类的行为，就可以描述继承自 Geom 包中提供的对象的新对象。

Finally, Geom objects can be shared within more complex data structures. This is why they are used within topological data structures, for example.

最后，Geom 对象可以在更复杂的数据结构中共享，例如，这就是它们在拓扑数据结构中使用的原因。

If a set of object instances is needed rather than a single object instance, TColGeom package can be used. This package provides instantiations of one- and two-dimensional arrays and sequences for curves from Geom package. All objects are available in two versions:

• handled by reference and
• handled by value.

如果需要对象实例集而非单个实例，可使用 TColGeom 包。该包为 Geom 包中的曲线提供一维和二维数组及序列的实例化。所有对象均有两种版本：

• 引用处理
• 值处理

The Geom package uses the services of the gp package to:

• implement elementary algebraic calculus and basic analytic geometry,
• describe geometric transformations which can be applied to Geom objects,
• describe the elementary data structures of Geom objects.

Geom 包使用 gp 包的服务来：

• 实现基本代数计算和基本解析几何，
• 描述可应用于 Geom 对象的几何变换，
• 描述 Geom 对象的基本数据结构。

However, the Geom package essentially provides data structures, not algorithms.

You can refer to the GC package to find more evolved construction algorithms for Geom objects.

但是，Geom 包本质上提供数据结构而非算法。

可参考 GC 包找到更高级的 Geom 对象构造算法。

Topology

OCCT Topology allows accessing and manipulating data of objects without dealing with their 2D or 3D representations. Whereas OCCT Geometry provides a description of objects in terms of coordinates or parametric values, Topology describes data structures of objects in parametric space. These descriptions use location in and restriction of parts of this space.

拓扑结构

OCCT 拓扑结构允许访问和操作对象数据，而无需处理其 2D 或 3D 表示。OCCT 几何通过坐标或参数值描述对象，而拓扑则描述参数空间中对象的数据结构。这些描述利用该空间内的位置和部分限制。

Topological library allows you to build pure topological data structures. Topology defines relationships between simple geometric entities. In this way, you can model complex shapes as assemblies of simpler entities. Due to a built-in non-manifold (or mixed-dimensional) feature, you can build models mixing:

• 0D entities such as points;
• 1D entities such as curves;
• 2D entities such as surfaces;
• 3D entities such as volumes.

拓扑库允许构建纯拓扑数据结构。拓扑定义简单几何实体之间的关系，通过这种方式可将复杂形状建模为简单实体的组合。由于内置非流形（或混合维度）特性，可构建混合以下元素的模型：

• 0D 实体（如点）；
• 1D 实体（如曲线）；
• 2D 实体（如曲面）；
• 3D 实体（如体）。

You can, for example, represent a single object made of several distinct bodies containing embedded curves and surfaces connected or non-connected to an outer boundary.

例如，可以表示由多个不同实体组成的单个对象，这些实体包含与外边界连接或不连接的嵌入曲线和曲面。

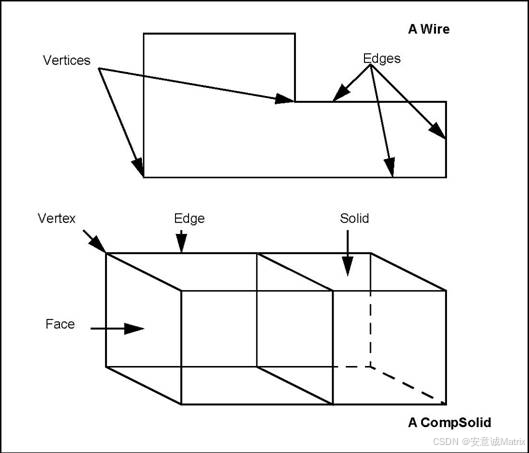
Abstract topological data structure describes a basic entity – a shape, which can be divided into the following component topologies:

• Vertex – a zero-dimensional shape corresponding to a point in geometry;
• Edge – a shape corresponding to a curve, and bound by a vertex at each extremity;
• Wire – a sequence of edges connected by their vertices;
• Face – part of a plane (in 2D geometry) or a surface (in 3D geometry) bounded by a closed wire;
• Shell – a collection of faces connected by some edges of their wire boundaries;
• Solid – a part of 3D space bound by a shell;
• Compound solid – a collection of solids.

The wire and the solid can be either infinite or closed.

抽象拓扑数据结构描述基本实体——形状，可分为以下组件拓扑：

• 顶点（Vertex）——对应几何中点的零维形状；
• 边（Edge）——对应曲线的形状，两端由顶点约束；
• 线框（Wire）——通过顶点连接的边序列；
• 面（Face）——由闭合线框约束的平面部分（2D 几何）或曲面部分（3D 几何）；
• 壳（Shell）——通过线框边界的某些边连接的面集合；
• 实体（Solid）——由壳约束的 3D 空间部分；
• 组合实体（Compound solid）——实体集合。

线框和实体可以是无限或闭合的。

A face with 3D underlying geometry may also refer to a collection of connected triangles that approximate the underlying surface. The surfaces can be undefined leaving the faces represented by triangles only. If so, the model is purely polyhedral.

具有 3D 基础几何的面也可指近似基础曲面的连接三角形集合。曲面可以未定义，仅由三角形表示面。在这种情况下，模型为纯多面体。

Topology defines the relationship between simple geometric entities, which can thus be linked together to represent complex shapes.

拓扑定义简单几何实体之间的关系，从而可将它们链接在一起表示复杂形状。

Abstract Topology is provided by six packages. The first three packages describe the topological data structure used in Open CASCADE Technology:

• TopAbs package provides general resources for topology-driven applications. It contains enumerations that are used to describe basic topological notions: topological shape, orientation and state. It also provides methods to manage these enumerations.
• TopLoc package provides resources to handle 3D local coordinate systems: Datum3D and Location. Datum3D describes an elementary coordinate system, while Location comprises a series of elementary coordinate systems.
• TopoDS package describes classes to model and build data structures that are purely topological.

抽象拓扑由六个包提供。前三个包描述 Open CASCADE Technology 中使用的拓扑数据结构：

• TopAbs 包为拓扑驱动应用提供通用资源，包含用于描述基本拓扑概念（拓扑形状、方向和状态）的枚举，并提供管理这些枚举的方法。
• TopLoc 包提供处理 3D 局部坐标系的资源：Datum3D 和 Location。Datum3D 描述基本坐标系，而 Location 包含一系列基本坐标系。
• TopoDS 包描述用于建模和构建纯拓扑数据结构的类。

Three additional packages provide tools to access and manipulate this abstract topology:

• TopTools package provides basic tools to use on topological data structures.
• TopExp package provides classes to explore and manipulate the topological data structures described in the TopoDS package.
• BRepTools package provides classes to explore, manipulate, read and write BRep data structures. These more complex data structures combine topological descriptions with additional geometric information, and include rules for evaluating equivalence of different possible representations of the same object, for example, a point.

另外三个包提供访问和操作此抽象拓扑的工具：

• TopTools 包提供用于拓扑数据结构的基本工具。
• TopExp 包提供探索和操作 TopoDS 包中描述的拓扑数据结构的类。
• BRepTools 包提供探索、操作、读取和写入 BRep 数据结构的类。这些更复杂的数据结构将拓扑描述与附加几何信息结合，并包含评估同一对象不同可能表示（如点）等效性的规则。

Shape content

The TopAbs package provides general enumerations describing the basic concepts of topology and methods to handle these enumerations. It contains no classes. This package has been separated from the rest of the topology because the notions it contains are sufficiently general to be used by all topological tools. This avoids redefinition of enumerations by remaining independent of modeling resources. The TopAbs package defines three notions:

• Type TopAbs_ShapeEnum;
• Orientation TopAbs_Orientation ;
• State StateTopAbs_State

形状内容

TopAbs 包提供描述拓扑基本概念的通用枚举和处理这些枚举的方法，不包含类。该包与拓扑的其余部分分离，因为其包含的概念足够通用，可被所有拓扑工具使用。这通过独立于建模资源避免枚举的重新定义。TopAbs 包定义三个概念：

• 类型 TopAbs_ShapeEnum；
• 方向 TopAbs_Orientation；
• 状态 StateTopAbs_State

Topological types

TopAbs contains the TopAbs_ShapeEnum enumeration,which lists the different topological types:

• COMPOUND – a group of any type of topological objects.
• COMPSOLID – a composite solid is a set of solids connected by their faces. It expands the notions of WIRE and SHELL to solids.
• SOLID – a part of space limited by shells. It is three dimensional.
• SHELL – a set of faces connected by their edges. A shell can be open or closed.
• FACE – in 2D it is a part of a plane; in 3D it is a part of a surface. Its geometry is constrained (trimmed) by contours. It is two dimensional.
• WIRE – a set of edges connected by their vertices. It can be an open or closed contour depending on whether the edges are linked or not.
• EDGE – a topological element corresponding to a restrained curve. An edge is generally limited by vertices. It has one dimension.
• VERTEX – a topological element corresponding to a point. It has zero dimension.
• SHAPE – a generic term covering all of the above.

拓扑类型

TopAbs 包含 TopAbs_ShapeEnum 枚举，列出不同拓扑类型：

• COMPOUND（组合体）——任何类型拓扑对象的组。
• COMPSOLID（组合实体）——由面连接的实体集合，将 WIRE 和 SHELL 的概念扩展到实体。
• SOLID（实体）——由壳限制的空间部分，三维。
• SHELL（壳）——由边连接的面集合，可开放或闭合。
• FACE（面）——2D 中为平面部分，3D 中为曲面部分，几何由轮廓约束（修剪），二维。
• WIRE（线框）——由顶点连接的边集合，根据边是否链接可为开放或闭合轮廓。
• EDGE（边）——对应约束曲线的拓扑元素，通常由顶点限制，一维。
• VERTEX（顶点）——对应点的拓扑元素，零维。
• SHAPE（形状）——涵盖上述所有的通用术语。

A topological model can be considered as a graph of objects with adjacency relationships. When modeling a part in 2D or 3D space it must belong to one of the categories listed in the ShapeEnum enumeration. The TopAbs package lists all the objects, which can be found in any model. It cannot be extended but a subset can be used. For example, the notion of solid is useless in 2D.

拓扑模型可视为具有邻接关系的对象图。在 2D 或 3D 空间中建模零件时，其必须属于 ShapeEnum 枚举中列出的类别之一。TopAbs 包列出任何模型中可找到的所有对象，不可扩展但可使用子集。例如，实体概念在 2D 中无用。

The terms of the enumeration appear in order from the most complex to the most simple, because objects can contain simpler objects in their description. For example, a face references its wires, edges, and vertices.

枚举术语按从最复杂到最简单的顺序排列，因为对象在描述中可包含更简单的对象。例如，面引用其线框、边和顶点。

Orientation

The notion of orientation is represented by the TopAbs_Orientation enumeration. Orientation is a generalized notion of the sense of direction found in various modelers. This is used when a shape limits a geometric domain; and is closely linked to the notion of boundary. The three cases are the following:

• Curve limited by a vertex.
• Surface limited by an edge.
• Space limited by a face.

方向

方向概念由 TopAbs_Orientation 枚举表示。方向是各种建模器中方向感的广义概念，用于形状限制几何域时，与边界概念密切相关。三种情况如下：

• 由顶点限制的曲线。
• 由边限制的曲面。
• 由面限制的空间。

In each case the topological form used as the boundary of a geometric domain of a higher dimension defines two local regions of which one is arbitrarily considered as the default region.

在每种情况下，用作更高维度几何域边界的拓扑形式定义两个局部区域，其中一个被任意视为默认区域。

For a curve limited by a vertex the default region is the set of points with parameters greater than the vertex. That is to say it is the part of the curve after the vertex following the natural direction along the curve.

对于由顶点限制的曲线，默认区域是参数大于顶点的点集，即沿曲线自然方向顶点之后的曲线部分。

For a surface limited by an edge the default region is on the left of the edge following its natural direction. More precisely it is the region pointed to by the vector product of the normal vector to the surface and the vector tangent to the curve.

对于由边限制的曲面，默认区域是沿边自然方向的左侧，更准确地说是曲面法向量与曲线切向量的向量积所指的区域。

For a space limited by a face the default region is found on the negative side of the normal to the surface.

对于由面限制的空间，默认区域位于曲面法线的负侧。

Based on this default region the orientation allows definition of the region to be kept, which is called the interior or material. There are four orientations defining the interior.

Orientation	Description
FORWARD	内部为默认区域。
REVERSED	内部为默认区域的互补区域。
INTERNAL	内部包含两个区域，边界位于材料内部（如实体内部的曲面）。
EXTERNAL	内部不包含任何区域，边界位于材料外部（如线框模型中的边）。

基于此默认区域，方向允许定义要保留的区域，称为内部或材料。有四种定义内部的方向：

方向	描述
FORWARD	内部为默认区域。
REVERSED	内部为默认区域的互补区域。
INTERNAL	内部包含两个区域，边界位于材料内部（如实体内部的曲面）。
EXTERNAL	内部不包含任何区域，边界位于材料外部（如线框模型中的边）。

The notion of orientation is a very general one, and it can be used in any context where regions or boundaries appear. Thus, for example, when describing the intersection of an edge and a contour it is possible to describe not only the vertex of intersection but also how the edge crosses the contour considering it as a boundary. The edge would therefore be divided into two regions: exterior and interior and the intersection vertex would be the boundary. Thus an orientation can be associated with an intersection vertex as in the following figure:

Orientation	Association
FORWARD	Entering
REVERSED	Exiting
INTERNAL	Touching from inside
EXTERNAL	Touching from outside

方向概念非常通用，可用于出现区域或边界的任何场景。例如，描述边与轮廓的相交时，不仅可描述相交顶点，还可将轮廓视为边界描述边如何穿过轮廓。因此边将分为两个区域：外部和内部，相交顶点为边界。因此，方向可与相交顶点关联，如下图所示：

方向	关联
FORWARD	进入（Entering）
REVERSED	退出（Exiting）
INTERNAL	从内部接触（Touching from inside）
EXTERNAL	从外部接触（Touching from outside）

Along with the Orientation enumeration the TopAbs package defines four methods:

除方向枚举外，TopAbs 包定义四种方法：

State

The TopAbs_State enumeration described the position of a vertex or a set of vertices with respect to a region. There are four terms:

Position	Description
IN	点在内部。
OUT	点在外部。
ON	点在边界上（在容差内）。
UNKNOWN	点的状态不确定。

状态

TopAbs_State 枚举描述顶点或顶点集相对于区域的位置，有四个术语：

位置	描述
IN	点在内部。
OUT	点在外部。
ON	点在边界上（在容差内）。
UNKNOWN	点的状态不确定。

The UNKNOWN term has been introduced because this enumeration is often used to express the result of a calculation, which can fail. This term can be used when it is impossible to know if a point is inside or outside, which is the case with an open wire or face.

引入 UNKNOWN 术语是因为此枚举常用于表示可能失败的计算结果。当无法知道点在内部或外部时（如开放线框或面的情况），可使用该术语。

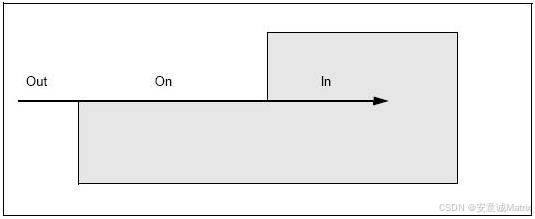
The State enumeration can also be used to specify various parts of an object. The following figure shows the parts of an edge intersecting a face.

状态枚举也可用于指定对象的各个部分。下图显示与面相交的边的各个部分。

Shape Location

A local coordinate system can be viewed as either of the following:

• A right-handed trihedron with an origin and three orthonormal vectors. The gp_Ax2 package corresponds to this definition.
• A transformation of a +1 determinant, allowing the transformation of coordinates between local and global references frames. This corresponds to the gp_Trsf.

形状位置

局部坐标系可视为以下任意一种：

• 具有原点和三个正交单位向量的右手三元组，gp_Ax2 包对应此定义。
• 行列式为 +1 的变换，允许局部和全局参考系之间的坐标变换，对应 gp_Trsf。

TopLoc package distinguishes two notions:

• TopLoc_Datum3D class provides the elementary reference coordinate, represented by a right-handed orthonormal system of axes or by a right-handed unitary transformation.
• TopLoc_Location class provides the composite reference coordinate made from elementary ones. It is a marker composed of a chain of references to elementary markers. The resulting cumulative transformation is stored in order to avoid recalculating the sum of the transformations for the whole list.

TopLoc 包区分两个概念：

• TopLoc_Datum3D 类提供基本参考坐标，由右手正交轴系或右手酉变换表示。
• TopLoc_Location 类提供由基本坐标组成的复合参考坐标，是由基本标记的引用链组成的标记，存储结果累积变换以避免重新计算整个列表的变换总和。

Two reference coordinates are equal if they are made up of the same elementary coordinates in the same order. There is no numerical comparison. Two coordinates can thus correspond to the same transformation without being equal if they were not built from the same elementary coordinates.

如果两个参考坐标由相同基本坐标按相同顺序组成，则它们相等，不进行数值比较。因此，如果两个坐标不是由相同基本坐标构建，即使对应相同变换，也不相等。

例如，考虑三个基本坐标：R1、R2、R3，复合坐标为：C1 = R1 * R2，C2 = R2 * R3，C3 = C1 * R3，C4 = R1 * C2。

注：C3 和 C4 相等，因为它们都是 R1 * R2 * R3。

TopLoc 包主要针对拓扑数据结构，但也可用于其他目的。