当前位置：首页 > news >正文

【数据结构】——二叉树--链式结构

news 来源：原创 2025/6/2 17:59:05

一、实现链式结构二叉树

二叉树的链式结构，那么从名字上我们就知道我们这个二叉树的底层是使用链表来实现的，前面我们的二叉树是通过数组来实现的，那么在其是完全二叉树的情况下，此时我们使用数组来实现就会使得其空间浪费较少，如果我们的普通的二叉树也使用数组来实现的话，那么其造成的空间浪费是非常大的。

使用链表来实现二叉树，其适用于所有的二叉树。

使用链式结构实现二叉树的方法为：链表中每个结点由三个部分组成，数据域、左孩子指针、右孩子指针。

其结构如下：

那么我们有了这个链式二叉树的结构后，那么我们要如何来实现链式结构二叉树呢？

那么我们首先就是创建二叉树的结点。

1、创建二叉树结点

结点的开辟和我们的链表是一样的，我们开辟的时候，要传的参数就是我们这个结点要存储的数据，然后我们这个结点通过二叉树结点指针返回即可，我们在创建的时候吗，别忘了对其初始化：

2、二叉树的遍历

二叉树的遍历分为三种方式：

1、前序遍历：先遍历根结点，然后是左结点，然后是右结点--(根左右)

如上的二叉树的前序遍历为：

A->B->D->NULL->NULL->NULL->C->E->NULL->NULL->F->NULL->NULL

2、中序遍历：先遍历左结点，然后是根结点，然后到右结点--(左根右)

如上的二叉树的中序遍历为：

NULL->D->NULL->B->NULL->A->NULL->E->NULL->C->NULL->F->NULL

3、后序遍历：先遍历左结点，然后遍历右结点，然后是根结点--(左右根)

如上的二叉树的后序遍历为：

NULL->NULL->D->NULL->B->NULL->NULL->E->F->C->A

那么我们要如何在代码中实现呢？

我们以前序遍历为例进行详细讲解：

首先我们不论是上面遍历，我们都需要这个二叉树的入口，那么我们的入口就是我们的根结点，所以我们的函数参数就是为树结点指针。

然后我们首先要进行判空，如果是空，那么我们就打印一个NULL，然后我们就终止这个函数。

如果不为空，那么我们就先将根结点的数据打印，然后我们去遍历左孩子，这是因为我们的前序遍历的顺序是根->左->右，那么我们就在这个函数中，递归调用，不过此时我们传入的参数就是根结点的左孩子了，那么其进入到左孩子后，一样还是重复的上面的操作，直到其遍历完成，然后左子树的遍历完成，那么我们就可以进入到根节点的右子树。其进入到右边子树后，还是按照根左右的顺序进行遍历即可，那么此时就可以使用我们的函数递归来实现：

其实际图解如下：

其函数栈帧如下：

代码如下：

那么我们的中序遍历，又是如何来遍历的呢？我们的中序遍历的顺序为左根右，那么我们可以这样，我们进入到函数，首先还是一样，先进行判空，如果为空就打印一个NULL，然后我们就递归到这个结点的左孩子，这是，然后其就进入到递归中，直到其一直递归到其左孩子是空的，那么此时就可以打印个NULL，然后就可以打印我们的根结点的值了，然后就到我们的右边孩子，进入到右边孩子后，我们这个函数还是会按照中序遍历的顺序，先去找其左孩子。

函数如下：

同理我们的后序遍历也是如此，按照其顺序--左右根进行递归，那么我们就先递归左孩子，然后递归右孩子，然后最后打印根结点的值。

代码如下：

上面就是链式结构二叉树的三种遍历方式。

3、链式结构二叉树的插入

我们的链式结构的二叉树的插入，那么我们的入口还是树的根结点，但是其如果为空，那么此时就使其为根结点即可，然后，如果其不为空的话，那么我们要如何进行插入呢？

我们用上面的树来举例，比如我们现在要插入的树是8，那么我们的入口是根结点，那么我们将其和当前的根结点进行比较，如果比其大，那么我们就将这个数据往其左结点处走，如果这个左结点无数据，那么就直接使其为左结点，即这个要插入的结点为这个函数的左子树的根结点，那么此时我们发现当其是大于根结点的值的时候，那么我们就让第一层的根结点的左孩子指向这个要插入的结点。那么同理，当其为小于的时候，那么我们就使其指向右孩子的指针指向递归函数，函数的参数为第一层函数的右孩子。

代码如下：

不过上面的话，对于二叉搜索树其可能不允许有重复的值，所以我们上面的代码只提供链式二叉树的数据插入的思路，仅供参考。

4、求二叉树的结点个数

我们的二叉树求结点个数，没办法像链表那样进行遍历求，那么我们是否也可以和上面一样，使用函数的递归来求呢？

我们使用一个树来分析一下：

和上面一样，我们从根结点为入口，然后我们递归的话，也是分为左右子树进行递归，那么我们递归结束的条件是什么呢？其实就是这个结点是空的时候，那么说明其不是结点，那么此时就结束递归即可，回到上一层递归，那么如果其不为空，那么就说明其是一个结点，那么我们的结点数就+1，那么我们的递归就可以返回一个1，还有其左右孩子的递归。

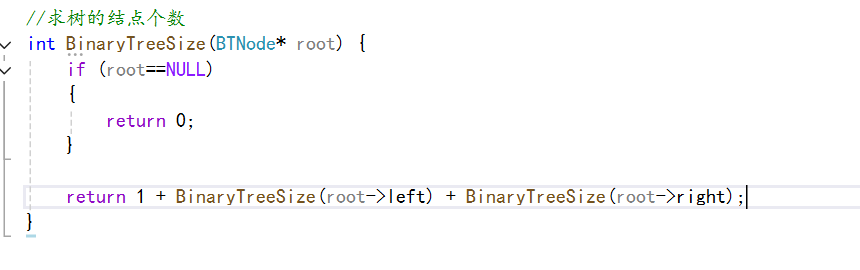
上面进行加1的原因是我们的根结点。

5、求叶子结点个数

前面我们讲过了，叶子结点就是其没有后继，即其指向左右孩子的指针都是为NULL的，那么我们这个可以作为一个条件，如果满足那么就为一个叶子结点，那么我们还是和上面一样进行递归其左右子树，如果其满足左右子孩子都是NULL，那么就返回1，如果其参数为NULL那么就返回0。

代码如下：

6、求第K层的结点个数

首先我们直到的是，如果树不为空，那么我们的第一层的结点个数为1，然后就是我们的第K层的结点个数=左子树的K-1层的结点个数+右子树的第K-1的结点个数。

那么我们可以使用函数的递归，使得k变成1的时候返回1，到空的时候也要终止递归。

代码如下：

7、求二叉树的高度

我们定义根节点的为第一层，然后我们知道，我们的二叉树的高度是左右子树中最大的一个，所以我们还是会想到使用递归左右子树的方法来进行，我们会很容易想到一个结束的条件，为空的时候返回0，然后就是我们要比较左右子树的高度，然后将大的值返回，且不要忘记+1，所以我们可以递归左右子树，分别找出左右子树的最大值，然后再进行比较。

代码如下：

8、二叉树查找值x的结点

那么我们就需要进行遍历二叉树，那么我们可以先遍历左子树，然后遍历右子树，如果在左子树没找到，那么我们再从右子树进行查找，如果没找到那么就返NULL，反之找到就返回这个结点的地址，然后如果是空树，那么就返回NULL。

代码如下：

9、链式结构二叉树的销毁

我们的销毁，那么我们还是需要遍历二叉树的每个结点，然后一个一个的进行内存释放，那么我们还是一样，对二叉树进行左右子树递归，然后当其不为空的时候就释放，为空的时候就终止函数。

可以发现我们销毁函数传递的是一个二级指针，这是因为我们要对一个指针进行修改，所以要使用地址传递才可以改变其实参的值。

二、二叉树的层序遍历

我们前面学习了二叉树的三种遍历方式，不过其是从左右子树来进行遍历，我们是否可以按照从上到下，从左到右的顺序实现二叉树的遍历呢？

要实现层序遍历，我们要借助前面学习的一个数据结构--队列。实现思路如下：

我们创建一个队列结构，其存储的是二叉树结构体，然后我们函数先将二叉树的根结点存储的数据入队，然后在进入一个循环，判断当前的队列是否为空，如果不为空，那么我们就入循环，此时我们打印队头的元素，然后将队头的元素出队，然后我们判断其是否有左孩子，如果有，那么就将其入队，然后再判断其是否有右边孩子，有的话也入队。如此反复。

代码如下：