第五章 宽松内存一致性模型 A Primer on Memory Consistency and Cache Coherence - 2nd Edition

第五章 宽松内存一致性模型

        前两章探讨了内存一致性模型中的顺序一致性（SC）和全存储序（TSO）。这些章节将 SC 描述为直观的模型，而 TSO 则被广泛实现（例如在 x86 架构中）。这两种模型有时被称为 “强一致性模型”，因为它们的全局内存顺序通常遵循（保留）每个线程的程序顺序。回顾可知，SC 对同一线程的两种内存操作的所有四种组合（加载→加载、加载→存储、存储→存储和存储→加载）都保留顺序，而 TSO 保留前三种顺序，但不保留存储→加载的顺序。

        本章将研究更宽松（弱）的内存一致性模型，这些模型旨在仅保留程序员 “需要” 的顺序。这种方法的主要优点是，通过减少对顺序的约束，可以允许更多的硬件和软件（编译器和运行时系统）优化，从而提升性能。主要缺点在于：宽松模型必须形式化定义何时需要顺序，并为程序员或底层软件提供机制，以向实现传达这种顺序要求；此外，不同厂商未能就单一的宽松模型达成一致，导致可移植性受损。

        对宽松一致性模型的全面探讨超出了本章的范围。本章旨在作为入门指南，提供基本概念，并帮助读者认识到对这些模型的简单理解存在局限性。具体而言，我们将介绍宽松模型的动机（5.1 节），提出并形式化一个示例宽松一致性模型 XC（5.2 节），讨论 XC 的实现，包括原子指令和用于强制顺序的指令（5.3 节），介绍无数据竞争程序的顺序一致性（5.4 节），介绍额外的宽松模型概念（5.5 节），呈现 RISC-V 和 IBM Power 内存模型的案例研究（5.6 节），指出进一步阅读材料和其他商业模型（5.7 节），比较不同模型（5.8 节），并简要提及高级语言内存模型（5.9 节）。

5.1 动机

        如我们即将看到的，掌握宽松一致性模型可能比理解 SC 和 TSO 更具挑战性。这些缺点引出了一个问题：为什么还要关注宽松模型？在本节中，我们将阐述宽松模型的动机，首先展示一些程序员不关心指令顺序的常见场景（5.1.1 节），然后讨论当不强制实施不必要的顺序时可以利用的一些优化（5.1.2 节）。

5.1.1 重排序内存操作的机会

        考虑表 5.1 中描述的示例。大多数程序员会期望 r2 始终获取值 “NEW”，因为 S1 在 S3 之前，S3 在动态实例 L1（加载值 “SET”）之前，而 L1 又在 L2 之前。我们可以表示为：

S1 → S3 → L1 加载 SET → L2。

        类似地，大多数程序员会期望 r3 始终获取值 “NEW”，因为：

S2 → S3 → L1 加载 SET → L3。

        除了上述两个预期的顺序外，SC 和 TSO 还要求 S1→S2 和 L2→L3 的顺序。保留这些额外的顺序可能会限制用于提升性能的实现优化，但程序的正确运行并不需要这些额外顺序。

        表 5.2 描述了一个更普遍的情况：两个使用同一锁的临界区之间的交接。假设硬件支持锁获取（例如，通过测试并设置进行读 - 修改 - 写操作，并循环直到成功）和锁释放（例如，存储值 0）。令核心 C1 获取锁，执行临界区 1（其中包含加载操作 L1i 和存储操作 S1j 的任意交织），然后释放锁。类似地，令核心 C2 执行临界区 2，包含加载操作 L2i 和存储操作 S2j 的任意交织。

        从临界区 1 到临界区 2 的正确交接取决于以下操作的顺序：

所有 L1i、所有 S1j → R1（释放锁）→ A2（获取锁）→ 所有 L2i、所有 S2j，
其中逗号（“,”）分隔顺序未指定的操作。

        正确操作不依赖于每个临界区内加载和存储操作的任何顺序 —— 除非这些操作针对同一地址（此时需要顺序以维持顺序处理器的顺序）。即：

所有 L1i 和 S1j 可以相对于彼此以任意顺序执行，
所有 L2i 和 S2j 可以相对于彼此以任意顺序执行。

        如果正确操作不依赖于许多加载和存储操作之间的顺序，那么或许可以通过放宽它们之间的顺序来获得更高的性能，因为加载和存储操作通常比锁获取和释放操作更频繁。这正是宽松或弱一致性模型的目标。

5.1.2 利用重排序的机会

        暂时假设一个宽松内存一致性模型：除非操作之间存在栅栏（FENCE），否则允许重新排序任何内存操作。这种宽松模型迫使程序员思考哪些操作需要排序，这是一个缺点，但它也支持许多可以提升性能的优化。我们将讨论一些常见且重要的优化，但深入探讨这一主题超出了本入门指南的范围。

非先进先出（Non-FIFO）合并写缓冲区

        回顾可知，TSO 允许使用先进先出（FIFO）写缓冲区，通过隐藏部分或全部已提交存储的延迟来提升性能。尽管 FIFO 写缓冲区能改善性能，但更优化的设计会使用非 FIFO 写缓冲区，以支持写操作的合并（即程序顺序中不连续的两个存储操作可以写入写缓冲区的同一条目）。然而，非 FIFO 合并写缓冲区通常会违反 TSO，因为 TSO 要求存储操作按程序顺序出现。我们的示例宽松模型允许存储操作在非 FIFO 写缓冲区中合并，只要这些存储操作未被栅栏分隔。
简化对核心投机执行的支持

        在强一致性模型的系统中，核心可能会在加载操作准备好提交之前，按程序顺序之外的顺序投机执行加载操作。回顾支持 SC 的 MIPS R10000 核心如何利用这种投机来获得比不进行投机的朴素实现更好的性能。然而，问题在于，支持 SC 的投机核心通常必须包含检查投机是否正确的机制，即使投机错误很少发生 [15, 21]。R10000 通过将逐出缓存块的地址与核心已投机加载但尚未提交的地址列表（即核心加载队列的内容）进行比较来检查投机。这种机制增加了硬件的成本和复杂度，消耗额外功率，并且代表了另一种可能限制指令级并行性的有限资源。在宽松内存一致性模型的系统中，核心可以按程序顺序之外的顺序执行加载操作，而无需将这些加载操作的地址与传入的一致性请求的地址进行比较。相对于宽松一致性模型，这些加载操作并非投机操作（尽管相对于分支预测或同一线程对同一地址的早期存储操作，它们可能是投机的）。

一致性与缓存一致性的耦合

        我们之前主张将一致性与缓存一致性解耦，以管理复杂度。另外，宽松模型可以通过 “打开缓存一致性的黑箱” 提供比强模型更好的性能。例如，实现可能允许部分核心从存储操作中加载新值，而其余核心仍可加载旧值，暂时打破缓存一致性的 “单写者 - 多读者” 不变式。这种情况可能发生在例如两个线程上下文逻辑上共享每个核心的写缓冲区，或两个核心共享 L1 数据缓存时。然而，“打开缓存一致性的黑箱” 会带来相当大的复杂度和验证挑战，让人联想到希腊神话中的潘多拉魔盒。如 5.6.2 节所述，IBM Power 允许上述优化。我们还将在第 10 章探讨为什么以及 GPU 和异构处理器如何在强制一致性的同时打开缓存一致性的黑箱。但首先，我们将探讨缓存一致性黑箱紧闭的宽松模型。

5.2 宽松一致性模型示例（XC）

        出于教学目的，本节介绍一个示例宽松一致性模型（XC），该模型体现了宽松内存一致性模型的基本思想和部分实现潜力。XC 假设存在全局内存顺序，这与 SC 和 TSO 等强一致性模型，以及已基本停用的 Alpha [33] 和 SPARC 宽松内存序（RMO）[34] 等宽松模型一致。

5.2.1 XC 模型的基本思想

        XC 提供了 FENCE（栅栏）指令，以便程序员指示何时需要顺序；否则，默认情况下加载和存储操作是无序的。其他宽松一致性模型将 FENCE 称为屏障（barrier）、内存屏障（memory barrier）、membar 或同步（sync）。假设核心 Ci 执行一些加载和 / 或存储操作 Xi，然后执行 FENCE 指令，接着执行更多加载和 / 或存储操作 Yi。FENCE 确保全局内存顺序中所有 Xi 操作先于 FENCE，而 FENCE 又先于所有 Yi 操作。FENCE 指令不指定地址，同一核心的两个 FENCE 也保持顺序。然而，FENCE 不影响其他核心的内存操作顺序（这也是 “栅栏” 比 “屏障” 更贴切的原因）。

        某些架构包含多个具有不同顺序属性的 FENCE 指令：例如，某架构可能包含一种 FENCE 指令，除了存储到后续加载的顺序外，强制其他所有顺序。但在本章中，我们仅考虑对所有操作类型都强制顺序的 FENCE。

XC 的内存顺序保证遵循（保留）以下程序顺序：

加载→FENCE
存储→FENCE
FENCE→FENCE
FENCE→加载
FENCE→存储

XC 仅对同一地址的两次访问保持 TSO 规则：

加载→同一地址的加载
加载→同一地址的存储
存储→同一地址的存储

        这些规则强制实现顺序处理器模型（即顺序核心语义），并避免出现让程序员困惑的行为。例如，“存储→存储” 规则可防止执行 “A=1然后A=2” 的临界区最终使 A 的值异常保持为 1；类似地，“加载→加载” 规则确保：若 B 初始为 0，另一线程执行 “B=1”，当前线程执行 “r1=B然后r2=B” 时，r1 和 r2 不会分别获取 1 和 0（仿佛 B 的值从新值变回旧值）。

        XC 确保加载操作立即看到自身存储的更新（类似 TSO 的写缓冲区旁路机制），该规则保留单线程的顺序性，避免程序员困惑。

5.2.2 XC 中使用 FENCE 的示例

        表 5.3 展示了程序员或底层软件应如何在表 5.1 的程序中插入 FENCE，使其在 XC 下正确运行。这些 FENCE 确保：

S1、S2 → F1 → S3 → L1 加载 SET → F2 → L2、L3。

        F1 作为排序存储的栅栏，对大多数读者而言是合理的，但部分人会惊讶于需要 F2 来排序加载操作。然而，若允许加载乱序执行，可能会使有序存储看起来像是乱序执行。例如，若执行顺序为 L2、S1、S2、S3、L1、L3，则 L2 可能获取值 0。这种结果在程序不包含 B1 控制依赖时更可能发生 —— 此时 L1 和 L2 是对不同地址的连续加载，看似可以重排序，但实际不行。

        表 5.4 展示了程序员或底层软件如何在表 5.2 的临界区程序中插入 FENCE，使其在 XC 下正确运行。为便于说明，这种在每次锁获取和锁释放前后都插入 FENCE 的策略较为保守（后续将说明部分 FENCE 可省略）。具体而言，FENCE F13 和 F22 确保临界区间的正确交接，因为：

        所有 L1i、所有 S1j → F13 → R11（释放锁）→ A21（获取锁）→ F22 → 所有 L2i、所有 S2j。

5.2.3 形式化定义 XC

        此处我们采用与前两章一致的符号和方法形式化定义 XC。仍用 L (a) 和 S (a) 分别表示对地址 a 的加载和存储操作，顺序 < p 和 < m 分别定义单处理器程序顺序和全局内存顺序。

        程序顺序 < p 是单处理器全序，描述每个核心逻辑上（顺序）执行内存操作的顺序；全局内存顺序 < m 是所有核心内存操作的全序。更形式化地说，XC 执行需满足以下条件：

        所有核心将加载、存储和 FENCE 插入 < m 时遵循：
若 L (a) <p FENCE，则 L (a) <m FENCE（加载→FENCE）
若 S (a) <p FENCE，则 S (a) <m FENCE（存储→FENCE）
若 FENCE <p FENCE，则 FENCE <m FENCE（FENCE→FENCE）
若 FENCE <p L (a)，则 FENCE <m L (a)（FENCE→加载）
若 FENCE <p S (a)，则 FENCE <m S (a)（FENCE→存储）
所有核心对同一地址的加载和存储插入 < m 时遵循：
若 L (a) <p L’(a)，则 L (a) <m L’(a)（同一地址：加载→加载）
若 L (a) <p S (a)，则 L (a) <m S (a)（同一地址：加载→存储）
若 S (a) <p S’(a)，则 S (a) <m S’(a)（同一地址：存储→存储）

每个加载操作获取同一地址中最后一次存储的值：
L (a) 的值 = <m 顺序中最大的 S (a) 的值，其中 S (a) <m L (a) 或 S (a) <p L (a)（类似 TSO）

表 5.5 总结了这些顺序规则，该表与 SC 和 TSO 的对应表差异显著。直观来看，表中显示仅当操作针对同一地址或使用 FENCE 时才强制顺序。与 TSO 类似，若操作 1 是 “存储 C”，操作 2 是 “加载 C”，存储可在全局顺序中晚于加载，但加载必须已看到新存储的值。支持 XC 执行的实现称为 XC 实现。

5.2.4 XC 正确运行的示例

        借助上一节的形式化定义，我们可解释 5.2.2 节的两个示例为何能正确运行。图 5.1a 展示了表 5.3 示例的 XC 执行：核心 C1 的存储 S1 和 S2 被重排序，核心 C2 的加载 L2 和 L3 也被重排序，但这些重排序均不影响程序结果。因此，对程序员而言，该 XC 执行等价于图 5.1b 所示的 SC 执行（其中两对操作未重排序）。

        类似地，图 5.2a 展示了表 5.4 临界区示例的执行：核心 C1 的加载 L1i 和存储 S1j 相互重排序，核心 C2 的 L2i 和 S2j 也相互重排序，这些重排序同样不影响程序结果。因此，程序员看到的 XC 执行等价于图 5.2b 所示的 SC 执行（无加载 / 存储重排序）。

        这些示例表明：通过插入足够的 FENCE，类似 XC 的宽松模型可对程序员呈现为 SC。5.4 节将从这些示例扩展讨论一般情况，但我们先探讨 XC 的实现。

5.3 实现 XC 模型

        本节讨论 XC 模型的实现。我们采用与前两章实现 SC 和 TSO 类似的方法，将核心操作的重排序与缓存一致性机制分离。回顾可知，TSO 系统中每个核心通过 FIFO 写缓冲区与共享内存隔离；而对于 XC，每个核心将通过更通用的重排序单元与内存隔离，该单元可对加载和存储操作进行重排序。

如图 5.3a 所示，XC 的工作流程如下：

        加载、存储和 FENCE 指令按核心 Ci 的程序顺序 < p 离开核心，并进入 Ci 重排序单元的尾部。
Ci 的重排序单元对操作进行排队，并按程序顺序或以下规则将其从尾部传递至头部：当 FENCE 到达重排序单元头部时会被丢弃。
当切换至核心 Ci 时，执行其重排序单元头部的加载或存储操作。

重排序单元需遵循三类规则：（1）FENCE 规则，（2）同一地址操作规则，（3）旁路规则：

FENCE 规则：FENCE 可通过多种方式实现（见 5.3.2 节），但必须强制顺序。具体而言，无论地址如何，重排序单元不得对以下操作重排序：
加载→FENCE、存储→FENCE、FENCE→FENCE、FENCE→加载、FENCE→存储。
同一地址操作规则：对同一地址，重排序单元不得重排序：
加载→加载、加载→存储、存储→存储。
旁路规则：重排序单元必须确保加载操作立即看到自身存储的更新。

        不难发现，这些规则与 5.2.3 节的形式化定义完全对应。在前两章中，我们指出 SC 和 TSO 实现中的切换器与内存可替换为缓存一致性内存系统，这一结论同样适用于 XC（如图 5.3b 所示）。因此，与 SC 和 TSO 类似，XC 实现可将核心（重）排序规则与缓存一致性机制分离 —— 缓存一致性机制实现全局内存顺序，而新的特性在于：由于重排序单元的重排序操作，内存顺序可能更频繁地违反程序顺序。

        从 TSO 迁移到 XC 这样的宽松模型能带来多少性能提升？遗憾的是，正确答案取决于 5.1.2 节讨论的因素，例如 FIFO 与合并写缓冲区的差异、投机执行支持等。20 世纪 90 年代末，本书作者之一曾认为投机核心的发展趋势会削弱宽松模型的存在意义（即性能优势），并主张回归 SC 或 TSO 的简单接口 [22]。尽管我们仍认同简单接口的优势，但这一趋势并未发生：一方面是企业惯性，另一方面，未来并非所有核心都会高度投机 —— 嵌入式芯片和 / 或多（非对称）核心芯片受功耗限制，可能无法支持复杂投机机制。

5.3.1 XC 中的原子指令

        在支持 XC 的系统中，实现原子读 - 修改 - 写（RMW）指令有多种可行方案，其实现方式也依赖于系统如何实现 XC。本节假设 XC 系统由动态调度核心组成，每个核心通过非 FIFO 合并写缓冲区连接至内存系统。

        在该 XC 系统模型中，一种简单可行的方案是借鉴 TSO 的实现：执行原子指令前，核心清空写缓冲区，获取具有读写一致性权限的缓存块，然后执行加载部分和存储部分。由于缓存块处于读写状态，存储部分直接写入缓存，绕过写缓冲区。在加载和存储操作之间（若存在时间窗口），缓存控制器不得逐出该块；若收到一致性请求，必须延迟处理，直至 RMW 的存储部分完成。

        借用 TSO 的方案实现 RMW 虽简单，但过于保守，会牺牲部分性能。值得注意的是，XC 允许 RMW 的加载和存储部分越过之前的存储操作，因此无需清空写缓冲区 —— 只需获取缓存块的读写权限，然后执行加载和存储操作，且在两者之间不释放该块即可。

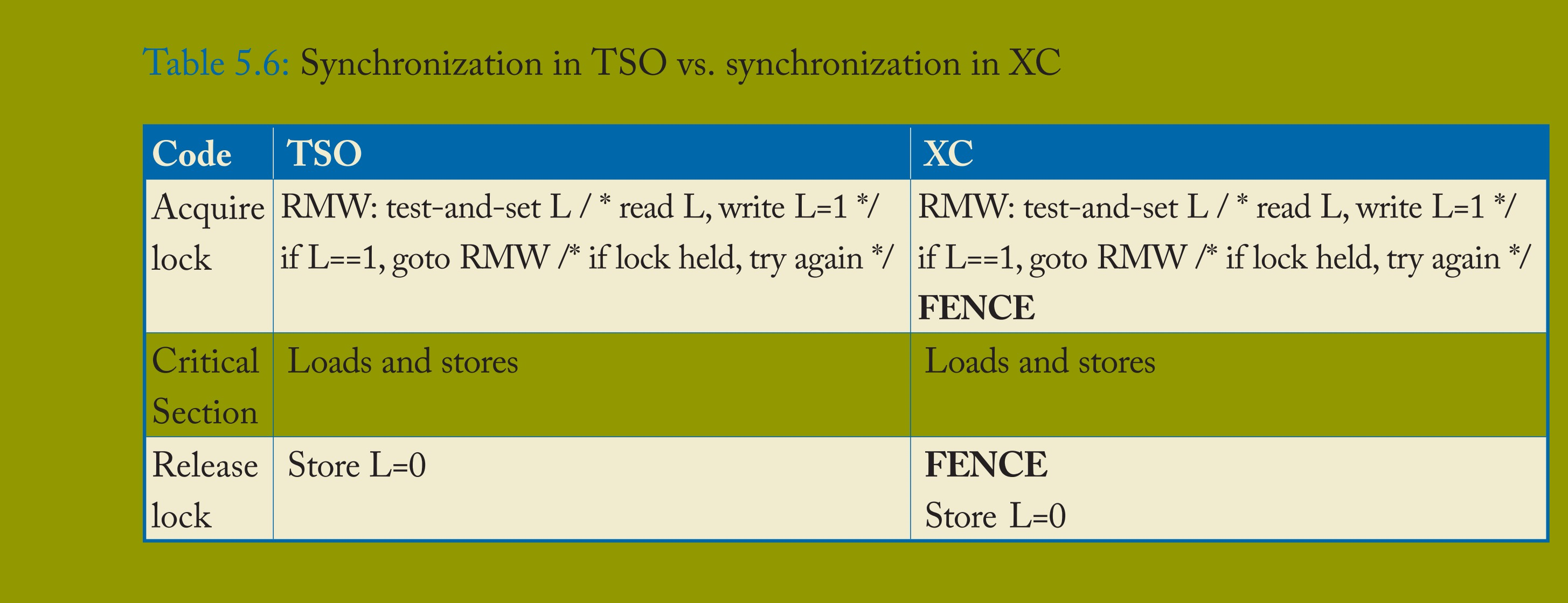
        其他原子 RMW 实现方案同样存在，但超出了本入门指南的范围。XC 与 TSO 的一个重要差异在于：原子 RMW 用于实现同步的方式不同。表 5.6 展示了 TSO 和 XC 下典型的临界区（包括锁获取和锁释放）：在 TSO 中，原子 RMW 用于尝试获取锁，存储指令用于释放锁；而在 XC 中，情况更为复杂 —— 默认情况下，XC 不限制 RMW 与临界区内操作的重排序，因此锁获取后必须跟随 FENCE；同理，锁释放前也必须插入 FENCE，以避免其与临界区内之前的操作重排序。

5.3.2 XC 中的 FENCE 实现

        若核心 C1 执行内存操作 Xi，然后执行 FENCE，再执行操作 Yi，XC 实现必须保证顺序 Xi <m FENCE <m Yi。有三种基本实现方式：

        类 SC 实现：将所有 FENCE 视为无操作（no-ops）。尽管尚未有商用产品采用此方案，但学术界已提出相关建议（如通过隐式事务内存 [16]）。
FENCE 作为清空操作：等待所有 Xi 操作完成后，视为 FENCE 执行完毕，再开始 Yi 操作。这种 “FENCE 即清空” 的方法较为常见，但会增加 FENCE 的开销。
激进式顺序强制：在不清空的前提下，强制保证 Xi <m FENCE <m Yi。具体实现方式超出了本指南的范围，但其设计和验证虽更复杂，却能比清空方式带来更好的性能。

        无论采用哪种方式，FENCE 实现必须明确每个 Xi 操作的完成时间（或至少顺序）。对于绕过常规缓存一致性的存储操作（如对 I/O 设备的存储，或使用特殊写更新优化的操作），确定其完成时间尤其困难。

5.3.3 注意事项

        最后需要强调：XC 实现者不能认为 “宽松模型意味着任何操作都可无序执行”。实际上，必须遵守 XC 的诸多规则，例如同一地址的加载→加载顺序（这在乱序核心中实现起来并非易事）。此外，所有 XC 实现必须足够 “强”，以确保在每条指令间都插入 FENCE 的程序呈现 SC 特性 —— 因为这些 FENCE 要求内存顺序完全遵循程序顺序。

5.4 无数据竞争程序的顺序一致性

        孩童与计算机架构师都希望 “鱼与熊掌兼得”。对于内存一致性模型而言，这意味着让程序员能用（相对）直观的 SC 模型进行推理，同时又能通过在 XC 这样的宽松模型上执行来获得性能优势。

        幸运的是，对于重要的无数据竞争（DRF）程序类 [3]，同时实现这两个目标是可能的。通俗地说，当两个线程访问同一内存位置，至少有一个访问是写入，且中间没有同步操作时，就会发生数据竞争。数据竞争通常（但并非总是）是编程错误的结果，许多程序员力求编写 DRF 程序。DRF 编程的 SC 要求程序员通过编写正确同步的程序并标记同步操作，确保程序在 SC 下是 DRF 的；然后要求实现者通过将标记的同步操作映射到宽松内存模型支持的 FENCE 和 RMW，确保 DRF 程序在宽松模型上的所有执行也都是 SC 执行。XC 和大多数商用宽松内存模型都有必要的 FENCE 指令和 RMW 来恢复 SC。此外，这种方法也为 Java 和 C++ 高级语言（HLL）内存模型（5.9 节）奠定了基础。

        让我们用两个例子来阐述 “DRF 的 SC” 动机。表 5.7 和表 5.8 都展示了核心 C1 存储两个位置（S1 和 S2），核心 C2 以相反顺序加载这两个位置（L1 和 L2）的例子。不同之处在于，表 5.7 中 C2 没有同步操作，而表 5.8 中 C2 获取了与 C1 相同的锁。

        由于表 5.7 中 C2 没有同步操作，其加载可以与 C1 的存储并发执行。由于 XC 允许 C1 重排序存储 S1 和 S2（或不重排序），C2 重排序加载 L1 和 L2（或不重排序），可能有四种结果：(r1, r2) = (0, 0)、(0, NEW)、(NEW, 0) 或 (NEW, NEW)。例如，当加载和存储按 S2、L1、L2、然后 S1 的顺序执行，或按 L2、S1、S2、然后 L1 的顺序执行时，就会出现 (0, NEW) 的输出。然而，这个例子包含两个数据竞争（S1 与 L2，S2 与 L1），因为 C2 没有获取 C1 使用的锁。

        表 5.8 描述了 C2 获取与 C1 相同锁的情况。在这种情况下，C1 的临界区将在 C2 的临界区之前完全执行，反之亦然。这允许两种结果：(r1, r2) = (0, 0) 或 (NEW, NEW)。重要的是，这些结果不受 C1 在其临界区内是否重排序存储 S1 和 S2，和 / 或 C2 在其临界区内是否重排序加载 L1 和 L2 的影响。“一棵树在森林里倒下（重排序的存储），但没有人听到（没有并发加载）。” 此外，XC 的结果与 SC 允许的结果相同。“DRF 的 SC” 从这两个例子中归纳出：

要么执行存在数据竞争，暴露 XC 对加载或存储的重排序，
要么 XC 执行是无数据竞争的，且与 SC 执行无法区分。

对 “DRF 的 SC” 更具体的理解需要一些定义：

某些内存操作被标记为同步（“同步操作”），其余默认标记为数据（“数据操作”）。同步操作包括锁获取和释放。
两个数据操作 Di 和 Dj 冲突，如果它们来自不同核心（线程）（即不由程序顺序排序），访问同一内存位置，且至少有一个是存储。
        两个同步操作 Si 和 Sj 冲突，如果它们来自不同核心（线程），访问同一内存位置（如同一锁），且至少有一个同步操作是写入（例如，自旋锁的获取和释放冲突，而读写锁的两个读锁不冲突）。
        两个同步操作 Si 和 Sj 传递冲突，如果 Si 和 Sj 冲突，或者 Si 与某个同步操作 Sk 冲突，Sk <p Sk’（即 Sk 在核心 K 的程序顺序中早于 Sk’），且 Sk’与 Sj 传递冲突。
        两个数据操作 Di 和 Dj 竞争，如果它们冲突，并且它们在全局内存顺序中出现时，没有来自相同核心（线程）i 和 j 的中间传递冲突同步操作对。换句话说，一对冲突的数据操作 Di <m Dj 不是数据竞争，当且仅当存在一对传递冲突的同步操作 Si 和 Sj，使得 Di <m Si <m Sj <m Dj。
SC 执行是无数据竞争（DRF）的，如果没有数据操作竞争。
程序是 DRF 的，如果其所有 SC 执行都是 DRF 的。
内存一致性模型支持 “DRF 程序的 SC”，如果所有 DRF 程序的所有执行都是 SC 执行。这种支持通常需要对同步操作采取一些特殊操作。

考虑内存模型 XC。要求程序员或底层软件确保所有同步操作前后都有 FENCE，如表 5.8 所示。

        通过在同步操作周围设置 FENCE，XC 支持 DRF 程序的 SC。虽然证明超出了本文的范围，但这个结果的直觉来自上述表 5.7 和表 5.8 中的例子。

        支持 DRF 程序的 SC 允许许多程序员用 SC 来推理他们的程序，而不是 XC 的更复杂规则，同时受益于 XC 比 SC 带来的任何硬件性能改进或简化。问题在于 —— 总是有问题 —— 在高性能下保证 DRF（即不将太多操作标记为同步）可能具有挑战性：

        精确确定哪些内存操作可能竞争，因此必须标记为同步，这是不可判定的。图 5.4 描绘了一个执行，其中核心 C2 的存储应该标记为同步 —— 这决定了 FENCE 是否真的必要 —— 但前提是能够确定 C1 的初始代码块是否不停止，当然，这是不可判定的。通过在不确定是否需要 FENCE 时添加 FENCE，可以避免不可判定性。这总是正确的，但可能影响性能。在极限情况下，可以在所有内存操作周围设置 FENCE，以确保任何程序的 SC 行为。

        最后，由于错误，程序可能存在违反 DRF 的数据竞争。坏消息是，数据竞争后，执行可能不再遵守 SC，迫使程序员推理底层宽松内存模型（如 XC）。好消息是，所有执行至少在第一次数据竞争之前都会遵守 SC，允许仅使用 SC 推理进行一些调试 [5]。

总之，使用宽松内存系统的程序员可以用两种方式推理他们的程序：

        他们可以直接使用模型对操作是否排序的规则进行推理（例如表 5.5 等），或者
他们可以插入足够的同步以确保没有数据竞争 —— 同步竞争仍然是允许的 —— 并使用相对简单的顺序一致性模型来推理他们的程序，该模型似乎从不按程序顺序执行内存操作。

        我们几乎总是推荐后者 “无数据竞争的顺序一致性” 方法，只让编写同步库或设备驱动程序等代码的专家使用前者方法。

5.5 宽松模型的若干概念

        学术文献中提出了许多不同的宽松内存模型与概念。在此我们从海量文献中梳理一些基础概念以帮助理解，但完整的形式化探讨超出了本入门指南的范畴。幸运的是，使用 “无数据竞争的顺序一致性”（SC for DRF）的程序员（可能是大多数）无需掌握本节的复杂内容，初次阅读时可略读或跳过。

5.5.1 释放一致性（Release Consistency）

        在 1990 年 ISCA 会议上，Adve 与 Hill 提出 “SC for DRF” 的同一分会场中，Gharachorloo 等人 [20] 提出了释放一致性（RC）。用本章的术语来说，RC 的核心观点是：在所有同步操作周围添加 FENCE 属于过度设计。若深入理解同步机制，同步获取操作仅需后续 FENCE，同步释放操作仅需前置 FENCE。

        以表 5.4 的临界区示例为例，FENCE F11、F14、F21 和 F24 可省略。聚焦于 “R11：释放锁”，FENCE F13 至关重要，因为它将临界区的加载（L1i）和存储（S1j）排序在锁释放之前；而 F14 可省略，因为若核心 C1 后续的内存操作（表中未显示）在释放 R11 前提前执行，也不会产生问题。

        与 XC 的 FENCE 双向强制顺序不同，RC 的 ACQUIRE 和 RELEASE 操作类似 FENCE，但仅单向排序内存访问：

ACQUIRE → 加载 / 存储（但加载 / 存储不强制排序 ACQUIRE）
加载 / 存储 → RELEASE（但 RELEASE 不强制排序加载 / 存储）
同时，RC 对 ACQUIRE 和 RELEASE 保持 SC 顺序：
ACQUIRE→ACQUIRE、ACQUIRE→RELEASE、RELEASE→ACQUIRE、RELEASE→RELEASE。

5.5.2 因果性与写原子性

此处阐释宽松模型的两个微妙特性：

        因果性：要求 “若我看到某事件并告诉你，你也应看到该事件”。例如表 5.9 中，核心 C1 执行存储 S1 更新 data1，核心 C2 自旋等待直到看到 S1 的结果（r1==NEW），执行 FENCE F1，然后执行 S2 更新 data2；核心 C3 自旋等待加载 L2 直到看到 S2 的结果（r2==NEW），执行 FENCE F2，然后执行 L3 观察 S1。若 C3 必定观察到 S1 已完成（r3==NEW），则因果性成立；若 r3=0，则因果性被违反。

        写原子性（也称存储原子性或多副本原子性）：要求核心的存储操作在逻辑上被所有其他核心同时看到。XC 定义中天然满足写原子性，因为其全局内存顺序（<m）规定了存储在内存中生效的逻辑原子点 —— 在此之前，其他核心不可见新值；在此之后，所有核心必须看到新值或后续存储的值，而不是被该存储覆盖的值。XC 允许核心在其他核心之前看到自身存储的值，这导致部分人认为 “写原子性” 这一名称不够准确。

        写原子性的必要非充分条件是正确处理 IRIW（独立读独立写）示例。表 5.10 中，核心 C1 和 C2 分别执行存储 S1 和 S2，若 C3 的 L1 观察到 S1（r1==NEW）且 C4 的 L3 观察到 S2（r3==NEW），但 C3 的 L2 加载 0（r2==0）且 C4 的 L4 加载 0（r4==0），则意味着 C3 先看到 S1 后看到 S2，C4 先看到 S2 后看到 S1—— 此时 S1 和 S2 不仅是 “重排序”，而是不存在全局顺序，写原子性被违反。反之未必成立：正确处理 IRIW 不自动意味着存储原子性。

更多细节（可能让人怀念 SC/TSO）：

        写原子性蕴含因果性。如在表 5.9 中，C2 观察到 S1 并执行 FENCE 后执行 S2，写原子性确保 C3 看到 S1 已完成。
        因果性不蕴含写原子性。表 5.10 中，若 C1/C3 与 C2/C4 分别共享写缓冲区，C1 将 S1 放入 C1-C3 缓冲区（仅 C3 可见），C2 将 S2 放入 C2-C4 缓冲区（仅 C4 可见），若 C3 的 L2 和 C4 的 L4 在存储离开缓冲区前执行，则违反写原子性，但该设计仍满足表 5.9 中的因果性。

XC 同时满足存储原子性和因果性 —— 前者由定义保证，后者因存储原子性蕴含因果性。

5.6 宽松内存模型案例研究

本节介绍两个内存模型案例：RISC-V 的 RVWMO 与 IBM Power 内存模型。

5.6.1 RISC-V 弱内存序（RVWMO）

        RISC-V 实现的 RVWMO 内存模型可视为释放一致性（RC）与 XC 的混合体。类似 XC，RVWMO 基于全局内存顺序（所有内存操作的全序）定义，并包含多种 FENCE 指令变体；类似 RC，加载 / 存储可携带注解：加载可带 ACQUIRE，存储可带 RELEASE，RMW 可带 RELEASE/ACQUIRE 或两者兼具。以下总结 RVWMO 如何融合 XC 与 RC 的特性，并讨论其在某些方面比 XC 更强、某些方面更弱的细节。

RELEASE/ACQUIRE 排序规则

        ACQUIRE 注解分为 ACQUIRE-RCP C 和 ACQUIRE-RCSC 两种，RELEASE 注解分为 RELEASE-RCP C 和 RELEASE-RCSC 两种。加载 / 存储可携带任意一种 ACQUIRE/RELEASE 注解，而 RMW 仅支持 RCSC 注解。注解保留以下顺序：

ACQUIRE → 加载 / 存储（ACQUIRE 包含两种类型）
加载 / 存储 → RELEASE（RELEASE 包含两种类型）
RELEASE-RCSC → ACQUIRE-RCSC
FENCE 排序规则

RVWMO 包含多种 FENCE 变体：

        强 FENCE 指令 FENCE RW,RW，类似 XC 的 FENCE，强制所有加载 / 存储顺序。
其他五种非平凡组合：FENCE RW,W、FENCE R,RW、FENCE R,R、FENCE W,W、FENCE.TSO。例如 FENCE R,R 仅强制加载→加载顺序，FENCE.TSO 强制加载→加载、存储→存储、加载→存储，但不强制存储→加载。
示例

表 5.11 中，核心 C1 的 S1→L1 由 RELEASE-ACQUIRE 强制排序，核心 C2 的 S2→L2 由 FENCE 强制排序，确保 r1 和 r2 不同时为 0。
依赖诱导的顺序

        RVWMO 在某些方面比 XC 更强：地址、数据和控制依赖可诱导内存顺序，而 XC 不支持。例如表 5.12 中，C1 通过 FENCE W,W 排序 S1（写 data2）和 S2（写指针），C2 的 L1（加载指针）和 L2（解引用指针）因地址依赖（L1 的结果作为 L2 的地址）被隐式强制 L1→L2。

表 5.13 的 “加载缓冲” 示例中，假设 x 和 y 初始为 0，XC 允许 r1 和 r2 同时读取任意值（如 42）：因 L1 与 S1、L2 与 S2 之间无 FENCE，XC 不强制加载→存储顺序，可能出现以下执行：

S1 预测 L1 将读 42，投机性向 y 写入 42；
L2 从 y 读 42 到 r2；
S2 向 x 写入 42；
L1 从 x 读 42 到 r1，使初始预测 “正确”。
而 RVWMO 因加载与后续存储存在数据依赖（加载值被存储使用），隐式强制 L1→S1 和 L2→S2，禁止上述行为。

        类似地，RVWMO 还隐式强制加载与受其控制依赖的后续存储之间的顺序，以避免因果循环（如表 5.14 中存储影响前置加载的取值）。需注意，上述依赖均指语法依赖（基于寄存器标识）而非语义依赖（基于实际值）。此外，RVWMO 还强制 “流水线依赖” 以反映处理器流水线实现，详情参考 RISC-V 规范 [31]。
同一地址的顺序

        RVWMO 与 XC 相同，强制同一地址的加载→存储、存储→存储顺序，不强制存储→加载；区别在于：RVWMO 并非在所有场景强制加载→加载顺序，仅当满足以下条件时生效：（a）两加载间无同一地址的存储；（b）两加载返回不同存储写入的值。具体原理参见 RISC-V 规范 [31]。
RMW 操作

RISC-V 支持两类 RMW：

        原子内存操作（AMO）：如 fetch-and-increment，要求加载和存储在全局内存顺序中连续，类似 XC 的 RMW。
保留加载 / 条件存储（LdR/StC）：由两条指令组成，LdR 获取值并设置保留，StC 仅在保留未失效时成功。其原子性语义更弱：若 LdR 读取由存储 s 产生的值，只要全局顺序中 s 与 StC 间无同一地址的存储，则 LdR/StC 视为原子。
总结

RVWMO 是融合 XC 与 RC 特性的新型宽松内存模型，完整的文字与形式化规范参见 RISC-V 规范 [31]。

5.6.2 IBM POWER 内存模型

        IBM Power 实现了 Power 内存模型 [23]（尤其参见第二卷第 1 章、4.4 节和附录 B）。在此我们尝试概述其核心思想，但确切细节请参考 Power 手册，特别是针对 Power 架构的编程指南。由于难以确保完整性，我们不会像 SC 那样提供类似表 5.5 的顺序表，且仅讨论常规可缓存内存（启用 “内存一致性”、禁用 “强制写通” 和 “禁止缓存”），不涉及 I/O 空间等场景。PowerPC [24] 是当前 Power 模型的早期版本。初次阅读时，读者可略读或跳过本节，该内存模型比本指南此前介绍的模型复杂得多。

Power 内存模型从表面看类似 XC，但存在以下重要差异：

第一，存储操作的执行顺序基于其他核心而非全局内存
        核心 C1 的存储针对核心 C2 “执行完成” 的定义是：C2 对同一地址的所有加载将看到新存储值或后续存储值，而非被覆盖的旧值。Power 确保：若 C1 通过 FENCE 将存储 S1 排序在 S2 和 S3 之前，则这三个存储对其他所有核心 Ci 的执行顺序一致。但若无 FENCE，C1 的存储 S1 可能已针对 C2 执行完成，却尚未针对 C3 执行完成。因此，Power 不保证如 XC 般存在全局内存全序（<m）。

第二，部分 FENCE 具有累积性
        核心 C2 执行内存操作 X1, X2,… 后执行 FENCE，再执行 Y1, Y2,…。设集合 X={Xi}，Y={Yi}（Power 手册分别称为 A 和 B）。累积性定义包含三层含义：

（a）将其他核心在 FENCE 前有序的操作加入 X（如 C1 的存储 S1 在 C2 的 FENCE 前针对 C2 执行完成，则 S1 加入 X）；
（b）将其他核心因数据依赖、控制依赖或其他 FENCE 在 FENCE 后有序的操作加入 Y；
（c）对（a）递归向前应用（如与 C1 操作有序的核心），对（b）递归向后应用。
（XC 的 FENCE 也具有累积性，但其行为由全局内存顺序自动保证，而非 FENCE 本身特性。）

第三，Power 支持多种 FENCE 类型（XC 仅一种）

        SYNC/HWSYNC（硬件同步）：将所有 X 操作排序在 Y 之前，具有累积性。
LWSYNC（轻量级同步）：确保 X 中的加载在 Y 中的加载前、X 中的加载在 Y 中的存储前、X 中的存储在 Y 中的存储前，具有累积性，但不保证 X 中的存储在 Y 中的加载前。
ISYNC（指令同步）：有时用于排序同一核心的两次加载，但不具累积性，且不同于 HWSYNC/LWSYNC，它排序的是指令而非内存访问，因此示例中不涉及。

第四，无 FENCE 时仍可能隐式排序
        例如，若加载 L1 的值用于计算后续加载 L2 的有效地址，则 Power 强制 L1→L2；若 L1 的值用于计算后续存储 S2 的有效地址或数据，则强制 L1→S2。
示例解析

        表 5.15（LWSYNC 应用）：核心 C1 通过 LWSYNC 将存储 S1、S2 排序在 S3 之前（无需保证 S1 与 S2 的顺序）；核心 C2 在条件分支 B1 后执行 LWSYNC，确保 L1 完成并赋值 r1=SET 后再执行 L2、L3。

        表 5.16（HWSYNC 在 Dekker 算法中的应用）：HWSYNC 确保 C1 的 S1 在 L1 前、C2 的 S2 在 L2 前，避免 r1=0 且 r2=0 的终止状态（LWSYNC 无法实现此约束，因它不强制存储→加载顺序）。

表 5.17（因果性示例）：C2 在 L1 看到 data1 新值后执行 LWSYNC F1，利用累积性将 S1 排序在 S2 前；C3 在 L2 看到 data2 新值后执行 LWSYNC F2，确保 S1 在 S2 前对 C3 可见，最终 L3 读取到 S1 的 NEW 值。

表 5.18（IRIW 示例）：通过 HWSYNC 的累积性强制 C1 的 S1 在 C3 的 L2 前、C2 的 S2 在 C4 的 L4 前，避免出现 r1=NEW、r2=0、r3=NEW、r4=0 的矛盾结果（LWSYNC 无法保证）。
Power 与 SC 的关系

        若在每条内存访问指令间插入 HWSYNC，Power 可模拟 SC 执行 —— 但这仅是思想实验，实际编程中此举会严重牺牲性能。

5.7 拓展阅读与商用宽松内存模型

5.7.1 学术文献

Dubois 等人 [18] 提出早期弱序模型；
Adve 与 Hill 将弱序推广为 “无数据竞争的 SC”[3,4]；
Gharachorloo 等人 [20] 提出释放一致性（RC）及 “正确标记” 理论；
Adve 与 Gharachorloo [2] 的内存模型教程总结了 20 世纪 90 年代中期的技术现状；
Meixner 与 Sorin [29] 首次证明通过重排序单元分离核心与缓存一致性系统可实现宽松模型。

5.7.2 商用模型

Alpha[33]：已停用，假设全局内存序，对 Linux 同步机制影响深远（因 Linux 曾运行于 Alpha 架构 [28]）。
SPARC RMO[34]：类似 XC 的全局序模型，但当前 SPARC 实现均采用更强的 TSO。
ARMv7[9,10]：内存模型与 Power 类似，不保证全局序，支持多种 FENCE；ARMv8[11] 转向多副本原子模型，类似 RISC-V RVWMO，支持 ACQUIRE/RELEASE 注解。

5.8 内存模型比较

5.8.1 宽松内存模型之间、与 TSO 和 SC 的关系如何？

        回顾可知：若内存一致性模型 Y 的所有 X 执行（实现）均为 Y 的执行（实现），但反之不成立，则 Y 比 X 更宽松（更弱）。此外，两个模型也可能无法比较，因为彼此都允许对方禁止的执行（实现）。

        图 5.5 沿用前一章的图示，其中 Power 替代了此前未指定的 MC1，MC2 可以是 Alpha、ARM、RMO 或 XC。它们的比较如下：

Power 比 TSO 更宽松，TSO 比 SC 更宽松。
Alpha、ARM、RMO 和 XC 比 TSO 更宽松，TSO 比 SC 更宽松。
        在有人证明 Power 与 Alpha、ARM、RMO、XC 中的某一模型存在宽松性包含关系或等价性之前，默认它们无法比较。

        Mador-Haim 等人 [26] 开发了一种自动比较内存一致性模型的技术（包括 SC、TSO 和 RMO），但未涉及 ARM 或 Power。ARM 与 Power 可能等价，但仍需证明。

5.8.2 宽松模型的优劣如何？

        如前章所述，优秀的内存一致性模型应具备 Sarita Adve 提出的 3P 原则，加上我们的第四项 P：

        可编程性（Programmability）：对于使用 “无数据竞争的 SC” 的开发者，宽松模型的可编程性可接受；但深入理解宽松模型（如编写编译器和运行时系统）仍具难度。
性能（Performance）：宽松模型性能优于 TSO，但在许多核心微架构中差异逐渐缩小。
可移植性（Portability）：遵循 “无数据竞争的 SC” 时可移植性可控；但突破宽松模型极限（尤其是不可比较的模型）时移植困难。
精确性（Precise）：许多宽松模型仅是非形式化定义，而形式化定义往往晦涩难懂。

总之…… 并没有简单的结论。

5.9 高级语言内存模型

        前两章及本章至今讨论的内存一致性模型属于硬件与底层软件的接口，关注（a）软件开发者的预期与（b）硬件实现的可能行为。

        为高级语言（HLL）定义内存模型同样重要，需明确（a）HLL 软件开发者的预期与（b）编译器、运行时系统及硬件实现的可行操作。图 5.6 展示了（a）高级与（b）低级内存模型的差异。

        由于许多 HLL 诞生于单线程时代，其规范未包含内存模型（还记得 Kernighan 和 Ritchie 的《C 程序设计语言》[25] 吗？）。Java 可能是首个具备内存模型的主流语言，但第一版存在缺陷 [30]。近年来，Java [27] 和 C++[14] 重新规范了内存模型，两者的核心均为 “无数据竞争的 SC”[3]—— 这得益于 Sarita Adve 参与撰写的三篇关键论文。为允许同步竞争但禁止数据竞争，程序员需将可能竞争的变量标记为同步（如使用 atomic 关键字），或通过 Java 的 synchronized 方法隐式创建同步锁。在任何情况下，只要无数据竞争程序遵循 SC，实现可自由重排序引用。

        具体而言，实现在同步访问之间可重排序或消除内存访问。图 5.7 展示了一个例子：图 5.7（a）为 HLL 代码，图 5.7（b）和（c）展示了核心 C1 的执行 —— 未分配寄存器时，以及变量 A 分配至寄存器 r1 后，加载 L3 被重排序并与 L1 合并。该重排序是正确的，因为 “无数据竞争的 SC” 保证其他线程无法观察到异常。除寄存器分配外，多数编译器和运行时优化（如常量传播、公共子表达式消除、循环拆分 / 融合、循环不变量代码移动、软件流水线和指令调度）均可重排序内存访问。由于 “无数据竞争的 SC” 允许这些优化，编译器和运行时系统生成的代码性能可接近单线程代码。

        若 HLL 程序意外或有意引入数据竞争？或专家程序员希望利用应用知识对同步操作施加最小（甚至无）顺序约束？此时其他线程可能观察到非 SC 执行。以图 5.7 为例，核心 C2（未显示）更新 A 和 C 时，C1 可能仅观察到 C 的更新而未观察到 A 的更新（因 A 被分配至寄存器），这在 HLL 层面违反 SC。

更普遍地，线程在数据竞争或非 SC 同步操作中能观察到的行为边界是什么？具体而言：

Java 要求为所有程序提供安全保证；
C++ 出于性能考虑，支持多种弱于 SC 的同步操作（称为低级原子操作）。

因此，Java 和 C++ 必须规范所有场景的行为，目标如下：

允许高性能 DRF 程序的所有优化；
明确指定所有程序的允许行为；
确保规范简洁清晰。

        我们认为：2005 年 Java 内存模型取得了显著进展，基本实现了目标（2），部分实现了目标（1）（但禁止了某些编译器优化 [32]），但未实现目标（3）。幸运的是，多数程序员可使用 “无数据竞争的 SC”，避开 Java 内存模型的 “暗角”；但编译器和运行时开发者必须深入理解这些细节 —— 例如：无论如何优化，对地址 A 的加载必须返回某时刻存储到 A 的值（可能是初始化值），而不是如 “表 5.13” 中凭空出现的 42。遗憾的是，这类复杂性并非个例 [12]。

同时满足上述三个目标仍是开放问题，C++ 领域正积极研究 [13,17]。
回顾测验问题 5

        “遵循高级语言一致性模型（如 Java）编写正确同步代码的程序员，无需考虑架构的内存一致性模型。” 该说法是否正确？
答案：视情况而定。对于典型应用程序员，答案为 “正确”，因其程序行为符合预期（即 SC）；对于编译器和运行时开发者，答案为 “错误”。
总结

        Java 和 C++ 等 HLL 采用 “无数据竞争的 SC” 的宽松内存模型思路。当这些 HLL 运行于硬件时，硬件内存模型是否也应宽松？

支持宽松硬件的理由：（a）性能更优；（b）编译器和运行时仅需将 HLL 同步操作映射为硬件低级同步操作和 FENCE 即可。
支持 SC/TSO 硬件的理由：（a）性能已足够好；（b）无需处理不可比模型的 FENCE，生成代码更具可移植性。

尽管争议尚未平息，但明确的是：宽松 HLL 模型不强制要求宽松硬件。