当前位置：首页 > news >正文

计算机组成原理第二章

news 来源：原创 2025/5/21 18:01:09

视频链接【2019版】2.1.1 进位计数法_哔哩哔哩_bilibili

进位计数法

我们在看这里十进制和二进制。在看乘法的时候9*9-81，还有0和其他相乘。差不多有100种情况。二进制则有4种 11，10，00，01

进制转换

思考问题，为什么十进制是叫十进制，如75

到了10，就进一位

那么如果是75.3呢

其他进制转换为10进制

知道了这个办法我们就可以将任意的其他进制转换成10进制了

不同进制之间的转换

将二进制转换为八进制和16进制，

在转换之前我们得先要明白一个事实，

我们还是以10进制作为我们的基准。对于十进制的3和八进制的3没有区别。但是对于10进制的13，如何转为为八进制呢。13是逢十便进1，所以我们在数数字的时候先数1，2，3，...到10，这个时候进一位即到了十位数。然后再数1，2，3。这便是个位数了。同样13对于八进制来说1，2，3...到了8往前进一位，然后数到5，那么就是15了。那么对于2 进制也是按照这个办法。

那么对于八进制的八如何用二进制来表示呢？111=1*2的2+1*2的1+1*2的0=7，所以我们提出了用

这样表示八进制的数

如

任意进制转换为十位数

十进制和其他进制转换

编码

BCD编码

出现的原因，总所周知，二进制更受计算机的青睐，但每次像这样

太麻烦了。

所以我们快速的方法就是建立表格一一对应8421码

解决方法

用二进制表示十进制的符号。

我们可以对其进行加法

但发现一个问题，它不在我们的查询表中，解决办法，强其移位

在这里加上六。产出的1 0011，然后再对前面进位。

有人会疑惑为什么要加六，我觉得是为了将其变为19，然后变为1*2的4+2+1=19，然后对其分割将不超过10的弄成0011，超过10的不就是1*2的4次方=16，减掉6变为原值，我乱说的，强背下来吧

BCD编码的其他几种

余3码很容易理解，就是加3.。至于2421码的话就是因为硬性规定，至于为什么不要深究。

在4以前规定最左边为0，右边的最高位为1并且只表示2，然后5-2=3弄成0011为1*2的1+1=3

Ascll码

需要知道的是（1），ASCLL编码以二进制存储，（2），大写字母连续存储，小写字母不连续

题目

大端小端模式

就是存储字节的高低

奇偶校验

产生缘由，信号在传输过程中产生突变，那么如何判断信号传输的准确性

解决办法，

在这里用00表示了A然后用01表示了b,而我们用的方案二的码字是用00表示a,11表示b.在方案1中码距为1，因为是在个位上有一个不同的，在方案二中码距为2.是因为十位和个位都有不同的。

不好的地方，如果00跳变为01，左边电脑想传输的是a,右边却接受成了b，右边不知道传错了。方案2，则如果00变为01，右边查到无这个，那么就明白错了，这只是知道错了的过程，还得需要纠错。马距越大，那么查到没有的越多，越容易发现传输错误。

采用解决办法，奇校验

奇教验保证每一段数据出现奇数个1，那么就是100，001.如果100信息错误变成101，不能保证是出现个奇数个1，知道传输错误了

奇偶校验题目

海明码校验

分组校验

给个题目理解一下啊

这里有4位，检验位位3位，对于检验位每位有01两种状态，即2的n次方

然后把原始数据填入

再根据海明码下标转换成二进制

看竖的有h3,h5,h7,

那么组成的是

我们在这里表示可以为偶校验

就这样变成了

纠错方程

将得到的检验位和原来的信息位结合

这里可以知道第二位出错了，我们把第二位取反就能知道了

循环代码

小总结一下

进制转换是为了了解如何用不同的编码来表示数据

校验码是为了解决在数据通信的过程传输中的错误，可以纠错

循环校验码

如何求呢

注：如果给出了二进制码是1101，然后让你求对应的多项式的话，生成多项式最高次幂是四位减去一位等于3.

后面再进行移位和相除

摸2除

被除数就是101001000，这后面三个0是补上去的，除数就是多项式前面系数1101

看减法，如果是相同填0，不同的话填1

然后再进行，将上面的0补位，往下移，1110的最高位是1，上位商也变成了1

在这里变成了0的情况，如

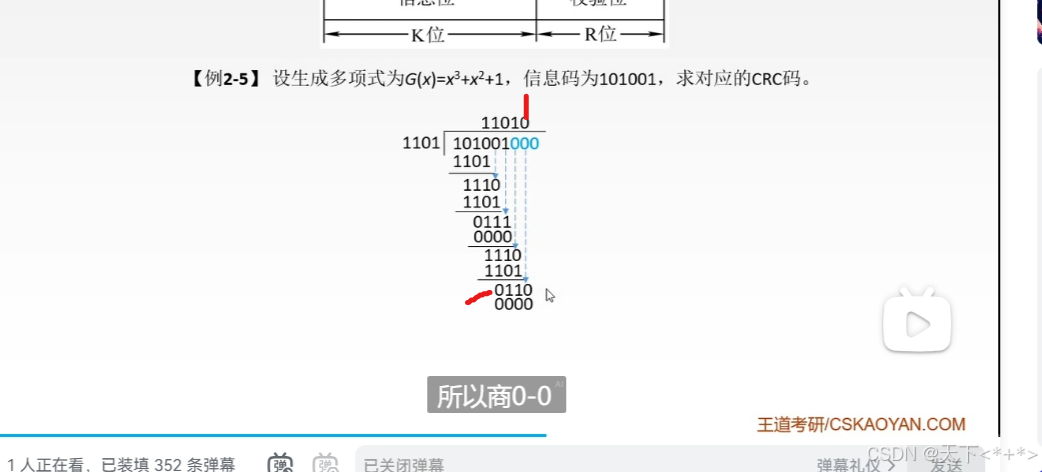
这里的最高位就是0，所以说上商就是0了

最后我们得到我们的检验位

发送对应的crc码

我们的纠错设计

本节概览

无符号数

无符号数表示的范围

有符号数的表示

对应定点的表示

同样我们只看绝对值并且，11是二进制的范围。十进制就是转换下。

n位数字呢

如果对应定点位置是在前面的话

原码这

计算机的加法

所以我们可以定义

补码反码移码

其分别作用

为什么要补码，在用源码进行加减运算的话

这里有个问题是符号难弄。

生活中调钟也是如此

那么这样的话我们据能够有无符号都能计算

补码规律

补码口诀

公式总结

补码范围

一张图表示

移码，能够解决比较数字的难题

也许这个能给我们一点启发

了解了，我们这里讨论的是8位有符号整数。对于8位有符号整数，其补码和移码的关系如下：
补码：对于正数，补码就是其原码；对于负数，补码是其原码取反后加1。
移码：对于任何数，移码是其补码的符号位取反。
现在，我们要找到十进制数 +2 在8位有符号整数中的补码和移码。
首先，找到 +2 的补码：
因为 +2 是正数，所以其补码就是其原码。
+2 的二进制表示是 00000010（前面6个0是因为我们使用8位来表示这个数）。
所以，+2 的补码是 00000010。
接下来，找到 +2 的移码：
移码是补码的符号位取反。
因为 +2 的补码是 00000010，其符号位是0，取反后变为1。
所以，+2 的移码是 10000010。
现在我们可以将这两个二进制数转换为十进制来验证它们的关系：
补码 00000010 对应的十进制数是 +2。
移码 10000010 对应的十进制数是 -126（因为在有符号整数中，最高位是1表示负数，其余位表示的是该负数的绝对值，所以 01111110 的十进制是 126，取反后是 -126）。
因此，对于十进制数 +2，其8位有符号整数的补码是 00000010，移码是 10000010，它们在十进制下分别对应 +2 和 -126，确实只相差一个符号位。

至于为什么不将移码直接算十进制

实际上，移码（或称为偏移码）并不是一个直接用于表示数值的编码方式，而是一种用于简化计算机硬件中算术运算的编码方式。移码通常用于计算机的算术逻辑单元（ALU）中，特别是在比较操作和分支指令中。
移码的定义是将一个数的补码的符号位取反而得来的。对于8位二进制数，移码和补码的关系如下：
对于正数和零，移码是将补码的符号位从0变为1。
对于负数，移码是将补码的符号位从1变为0。
移码的“移”是指将所有的数值在二进制表示上向正方向移动了一个固定的偏移量。对于8位二进制数，这个偏移量通常是2^7（即128）。因此，移码10000010实际上表示的是128 + 2 = 130，但是我们不能直接这样解读，因为移码并不是用来直接表示数值的。
以下是为什么不能直接将移码10000010转换为十进制的几个原因：
定义问题：移码的定义是基于补码的，而不是直接表示数值。它的目的是为了简化计算机内部的运算。
符号位：在移码中，符号位并不直接表示正负，而是用于算术运算。例如，如果两个移码相加，其结果仍然是一个有效的移码。
偏移量：移码中的数值是相对于一个固定偏移量（如128）来表示的。这意味着，如果你直接将移码转换为十进制，而不考虑这个偏移量，你会得到一个错误的结果。
硬件实现：在计算机硬件中，使用移码可以简化比较操作。例如，如果两个移码相减，其结果可以直接用于条件分支指令，而不需要额外的步骤来处理符号位。
因此，如果你想从移码得到一个数的十进制值，你需要先将移码转换回补码，然后再将补码转换为十进制。以下是转换过程：
移码：10000010
补码（将移码的符号位取反）：01111110
十进制值（将补码转换为十进制）：-126
在这个例子中，移码10000010实际上表示的是补码01111110，而补码01111110表示的是十进制数-126。因此，移码10000010对应的十进制数是-126，而不是直接将二进制数转换为十进制得到的130。