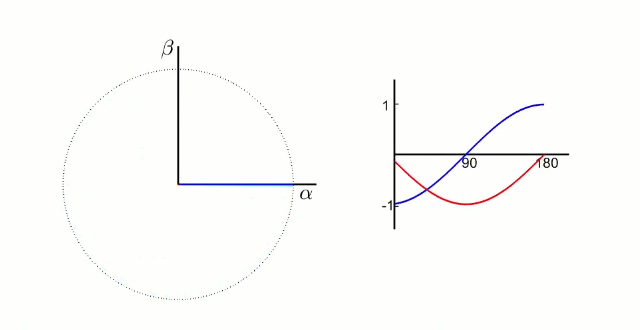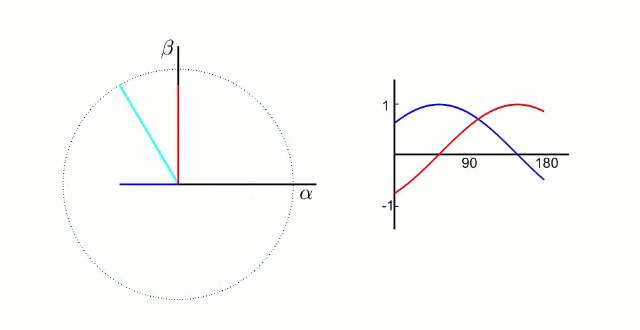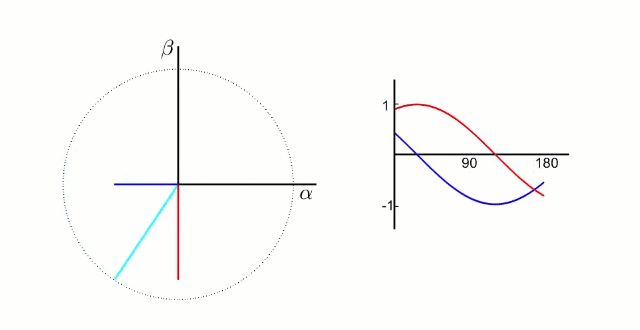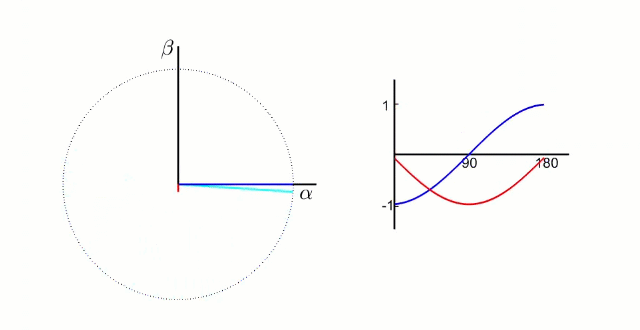永磁同步电机公式总结——反电动势、磁链、转矩公式;三项、两项电压方程;坐标表换方程
一、电机的一些基础公式和概念
1.1 反电动势相关
1.1.1 反电动势电压与输入电压关系
反电动势不会高于输入电压
= 供给电机的电压
= 反电动势的电压
= 电机自身的内阻所消耗的电压
1.1.1 反电动势公式
= 反电动势
= 线圈匝数
= 磁场的变化率 (T)
= (θ 为磁场方向与线圈法向的夹角)
=
(磁通量)
= 线圈截面积 (
)
= 产生磁场变化所经历的时间 (s)
1.1.2 电机定子绕组的功率关系
= 电源供给给电动机的功率(输入功率)
= 电动机输出的机械功率
= 热功损(铜损、铁损、机械损等)
1.1.3 电机定子绕组电流公式
= 反电动势
= 外加电压
= 表示电动机回路总电阻
1.2 安培力相关
安培力公式:
= 表示磁感应强度
= 表导体棒的长度
= 导体棒切割的速度
常理可知,电机反电动势不会大于供给的电压,加入我们给电机输入10V 电压,反电动势将不会超过 10V。
对于一个电机参数来说,B 和 L 是已知的,E 也不会超过输入电压,我们就可以根据这个公式推算出 v,进而得到电机空转的理论的最大值。
1.2 磁链相关
1.2.1 电机磁链常数定义 ( )
)
定义: 是永磁体在定子绕组中产生的固定磁链幅值,单位为韦伯 (Wb)。其大小由永磁体的材料特性(如剩磁 Br)、体积和充磁方向决定,理想情况下为常数,但实际受温度影响 (如钕铁硼永磁体温度每升高100℃,下降10%~15%)
电机旋转时, 切割定子绕组产生反电动势:
= 反电动势
= 电角速度
1.2.2 电机绕组磁链定义(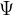 )
)
绕组磁链是指定子绕组中由电流和永磁体共同作用产生的总磁通量,单位为韦伯 (),随电流、转子位置 (
) 和时间变化,是电机控制的核心变量。
- 感磁链:由定子电流通过绕组自感 (
) 产生。
- 互感磁链:其他绕组电流通过互感耦合产生(如三相绕组间的相互作用)。
- 永磁体耦合磁链:永磁体磁场在定子绕组中的投影分量 (
)。
1.3 转矩方程
对于嵌入式永磁同步电机 (IPMSM) 力矩方程是:
= 永磁转矩,与q轴电流成正比
= 磁阻转矩,由 d-q 轴电感差异和电流交互作用产生。
表贴式 (SPMSM) 则是:
因为 其磁阻转矩为 0,所以控制表贴式电机获得最大转矩控制 id=0 即可。
二、定子三项电压方程:
2.1 定子三项电压方程 (磁链表达)
= 相电压
= 相电流
= 相磁链
= 相电阻
三项矩阵形式如下,其中 P 为微分算子:
其中,、
、
是三相定子电压,
是定子电阻,是是子电流,
、
、
是定子磁链,
、
、
。为电角度和实际电机角度不同,此方程组电机控制过程中应用情况较少。注意:定子磁链是一个多变量、强耦合的结果,所以用电桥测试电感时,慢速旋转电机,电感的值一直在变化。
2.2 磁链方程
电机的磁链电流产生和永磁体与绕组有关:

、
、
= 转子永磁体磁链常数
、
、
= 各自绕组的自感
、
、
= 相间互感,对称系统中
、
、
= 三项定子电流
= 永磁体磁链幅值 (常数)
= 转子 d 轴与 A 相绕组的电角度
对于 B、C 相的反电动势和角度的关系正好是相差 120°,所以上述公式需要减去和加上 。

2.3 磁链方程的微分形式
简化之前的磁链方程,此方程只描述静态系统所以忽略角度:
= 定子绕组的电感,包括自感和互感
= 永磁体磁链幅值 (常数)
如果看做成一个动态系统需要加入电角度:
我们将其取微分可得:
其中 (转子电角速度),因为最终取微分可得:
= 永磁体磁链幅值 (常数)
= 定子绕组的电感,包括自感和互感
= 电角速度
2.3 定子三项电压方程 (电感微分与磁链峰值常数表达)
还是回到这个方程:
其中磁链等于:
也就是对 取微分可得:
![]()


所以最终我们得出:

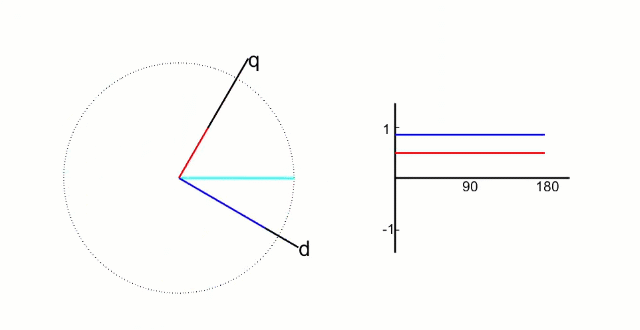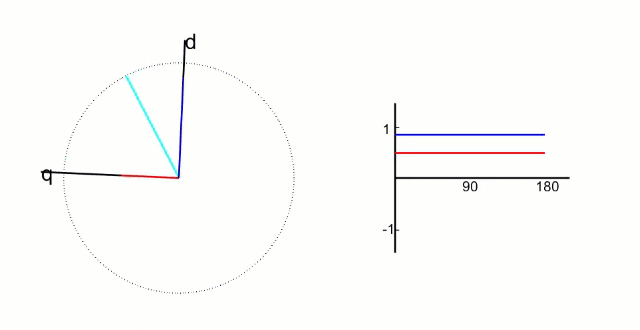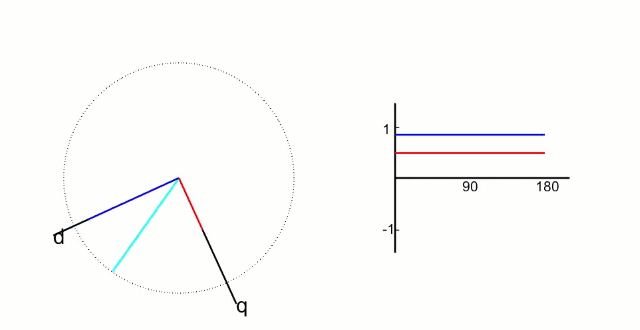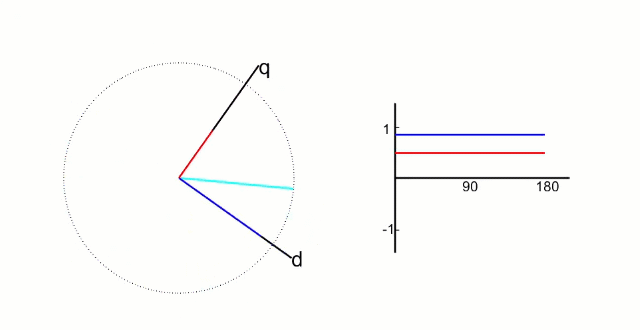
其中  矢量图如下:
矢量图如下:

三、两项电机方程
3.1 α 和 β 轴的静止电压方程
对 ABC 三相电压方程做 Clake 变换得到 uα、uβ 静止电压方程。

eα、eβ 是两轴反电动势的公式。

这两个方程一般用作无传感器角度观测,需牢记,表贴式电机 、
相等,内嵌式电机
、
不相等。
3.2 d 和 q 轴旋转坐标电压方程
再做 Park 变换得到两项电压 d、q 轴下的电压方程。


3.3 d 和 q 轴的磁链方程
对于 IPMSM 电机来说 dq 轴电感不相同,公式如下:

SPMSM 电机 dq 电感轴相等,简化为:
![]()
4.2 d 和 q 轴的电磁转矩方程
= d 轴电感
= q 轴电感
= 磁链常数
= 极对数
= 电机转矩
其中,、
、
为电机本体参数,需测定。
为电机极对数。此方程已完成对耦合量解耦,最后一项和转速有关的磁链耦合量,可前馈消除,如果影响比较小,可以不用管。轴方程需牢记,电机实际控制需要用到,电流环,MTPA,弱磁等都需用到此方程。
四、坐标变换
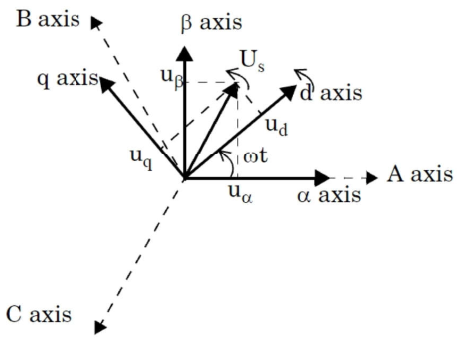
4.1 Clark 变换和逆 Clark 变换
4.1.1 Clark 变换
左图是 A、B、C 三项电流;右图是 α、β 两项电流
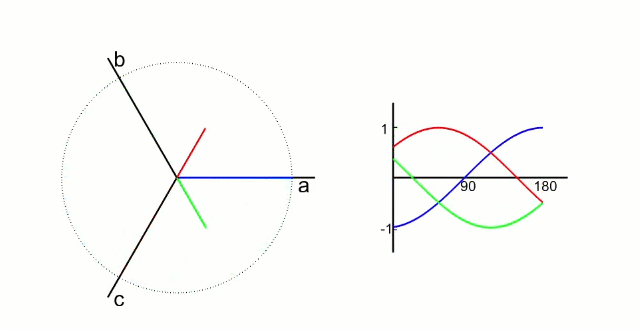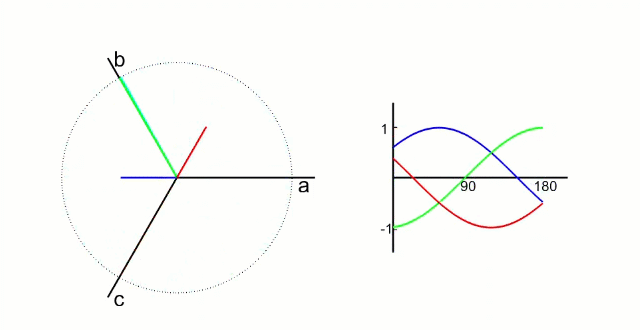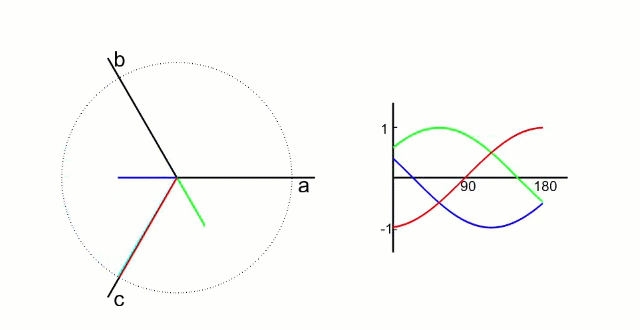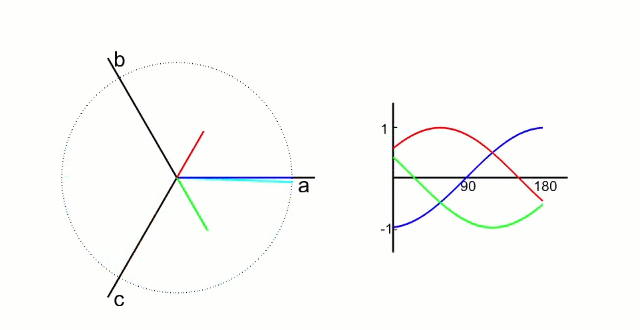
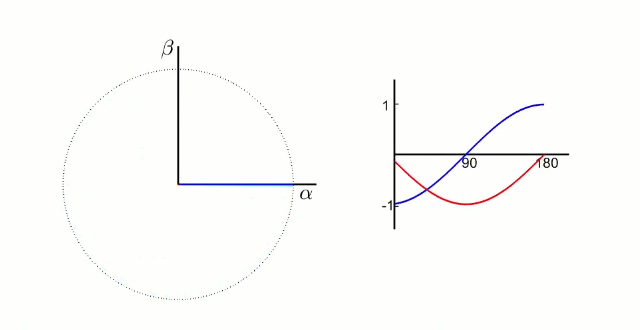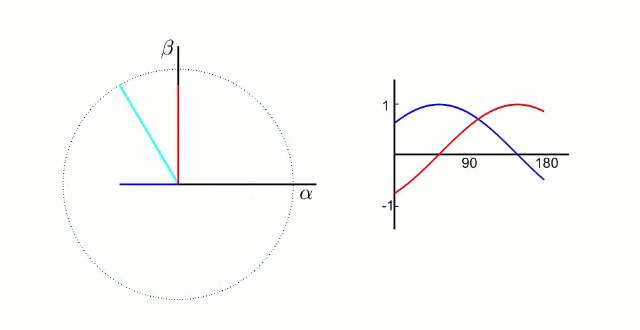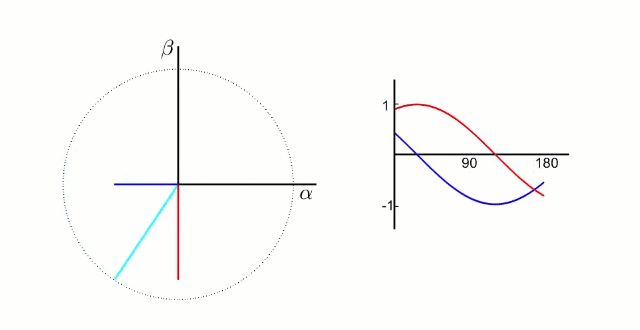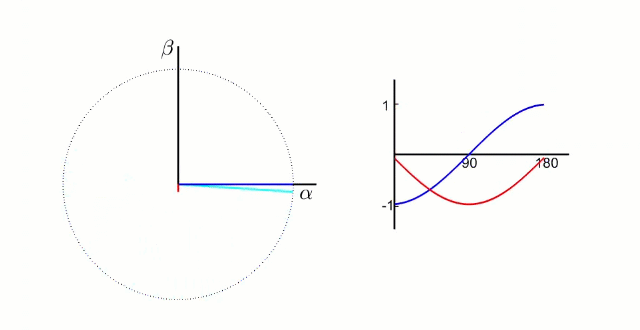
以电流变换为例,A、B、C 向 α、β 轴变换,按照幅值不变原则:
4.1.2 逆 Clark 变换
以电流变换为例,α、β 向 A、B、C 轴变换,按照幅值不变原则:
4.2 Park 变换和逆 Park 变换
左图是 α、β 两项电流;右图是 DQ 轴电流