当前位置：首页 > news >正文

math toolkit for real-time development读书笔记一三角函数快速计算(2)

news 来源：原创 2025/5/18 6:45:46

续math toolkit for real-time development读书笔记一三角函数快速计算(1)

在介绍更好的实现方法之前，先花点时间讨论一个简单的实现可能会有所帮助。总体思路非常直接：

1.首先，要知道由于函数在 360°（2π 弧度）后会重复，因此不应使用过大的值调用这些函数。但我无法保证不会有人这样做，所以我会执行取模运算.这至少能保护我免受像 10,000π 这样的不合理输入的影响。请注意，此操作的结果应始终产生一个 0 到 2π 范围内的正角度。

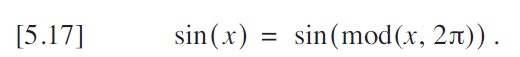
其次，正弦函数是奇函数，因此

如果角度大于 180°（π 弧度），我只需减去 π，然后记住改变结果的符号。

第三，正弦函数和余弦函数是互补的。因此：

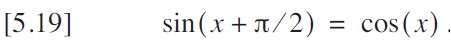
通过这样做，我将范围缩小到 0° 到 90°（π/2 弧度）。最后，我可以以略微不同的形式再次利用互补性来写出：

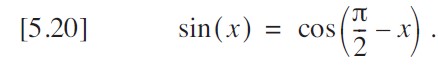
如果角度大于 45°（π/4 弧度），我会用 90° 减去该角度，得到一个小于 45° 的角度。这种变换有两个作用：一是将范围缩小到 0° 到 45°，二是确保我在目标范围内使用两个级数（方程 [5.15] 或 [5.16]）中精度最高的那个。所有这些逻辑最好地体现在如下的伪代码中。虽然原理简单，但实现起来相当繁琐。我实际上见过有人直接按这种方式实现正弦函数，着急的时候我自己也这么做过。但嵌套的函数调用自然会浪费计算机时间，而且代码执行的符号变换和角度变换比实际需要的更多。就连实变量模运算函数 mod () 的实现也不简单。我可以消除嵌套函数调用，但取而代之的要么是杂乱的嵌套 if 语句，要么是需要设置和测试的几个标志位。这些方法都不太令人满意。

伪代码：

double sine(double x) {x = mod(x, twopi);if( x > pi){return - sin1(x - pi);elsereturn sin1(x);
}
double sin1(double x) {if (x > halfpi)return cos2(x - halfpi);elsereturn sin2(x);
}
double sin2(double x) {if (x > pi_over_four)return _cosine(halfpi - x);elsereturn _sine(x);
}
Function cos2(x) {if (x > pi_over_four)return _sine(halfpi - x);elsereturn _cosine(x);
}

请注意基础函数的名称变化；为了将它们与全范围函数区分开，我在它们的名称前加了一个下划线。

幸运的是，有一个非常简洁的解决方案可以消除所有问题，甚至无需使用模运算（mod ()）。该方案的部分关键在于，实际上我不必将角度限制为正值。查看方程 [5.7] 和 [5.8] 可以发现，它们对负参数同样有效。

算法的其余部分请参见图 5.3。乍一看，单位圆似乎被划分为八个卦限，但仔细观察会发现它仅分为四个 90° 的象限，每个象限以 x 轴和 y 轴为中心。这些象限相对于常规位置逆时针旋转了 45°。每个象限内标注了计算该角度正弦值所需的公式。

如图所示，我将为每个象限分配一个 0 到 3 的编号。如果使用舍入而非截断来获取整数，这个编号可以非常快速地计算出来。

然后，我可以通过减去适当的值将角度简化为其核心部分。请注意，此公式会将任何角度（无论是正值还是负值）缩小到–45° 到 45° 的范围。象限编号可通过计算 n mod 4 得到。

传统单位圆以坐标轴为边界划分为四个标准象限（每个 90°，边界为 x/y 轴）。
旋转 45° 的象限划分则以坐标轴的角平分线为边界，将单位圆划分为四个倾斜的象限，每个象限仍覆盖 90°，但中心轴为x 轴、y 轴、y=x 轴、y=-x 轴（即原坐标系旋转 45° 后的方向）。

（示意图说明：象限 0 中心为 x 轴，象限 1 中心为 y=x 轴，象限 2 中心为 y 轴，象限 3 中心为 y=-x 轴）

具体方法是：

将角度转换为弧度之后，通过下述公式快速定位象限的编号。

$n=Round(\frac{\theta }{\frac{\pi }{2}}) =\left \lfloor \theta /(\frac{\pi }{2})) +0.5\right \rfloor\div 4$

使用四舍五入（round）而非截断，可避免边界角度的象限误判（如 π/2 严格属于象限 1 而非象限 0）,这里的除号表示取余操作

2.根据象限编号 n，从 θ 中减去对应象限的中心角度，公式为： $\theta{}'= \theta -n*\frac{\pi }{2},n\in {0,1,2,3}$ .例如：

象限 1 中心为 90°=π/2，约简后角度为 θ−π/2
象限 2 中心为 180°=π，约简后角度为 θ−π
象限 3 中心为 270°=3π/2，约简后角度为 θ−3π/2
象限 0 无需调整，直接使用原始约简值

3.每个倾斜象限内的正弦值可通过三角恒等式转换为标准三角函数组合，避免复杂运算。

现在，一个简单的 case 语句即可为每种情况提供所需的结果。最终的代码如下所示。请注意，我无需单独进行一组计算来求余弦值，只需将角度加上 90°（π/2 弧度）并调用正弦函数即可。通过这种方法，我最终在单个步骤中处理了模运算和角度约简，并且将符号变换和逻辑操作降至最少。

double sine(double x){
long n = (long)(x/halfpi + 0.5);
x -= n * halfpi;
n = mod(n, (long)4);
switch(n){case 0:return _sine(x);case 1:return _cosine(x);case 2:return - _sine(x);case 3:return - _cosine(x);}
}
double cosine(double x){return sine(x + halfpi);
}

将角度约简到小于 45° 的范围相当容易。从表 5.4 和 5.5 可以看出，要获得双精度精度需要九项（计算）。我希望进一步减少项数，但接下来一个明显的问题是：我能做到吗？答案是：可以，但并非没有代价。

所有的范围约简都可以从一个单一的三角恒等式推导而来。

$\sin(A+B)=\sin A\cos B+\cos A\sin B$

如果令 A = x 且 B = π/6，划分为正负15°范围时：

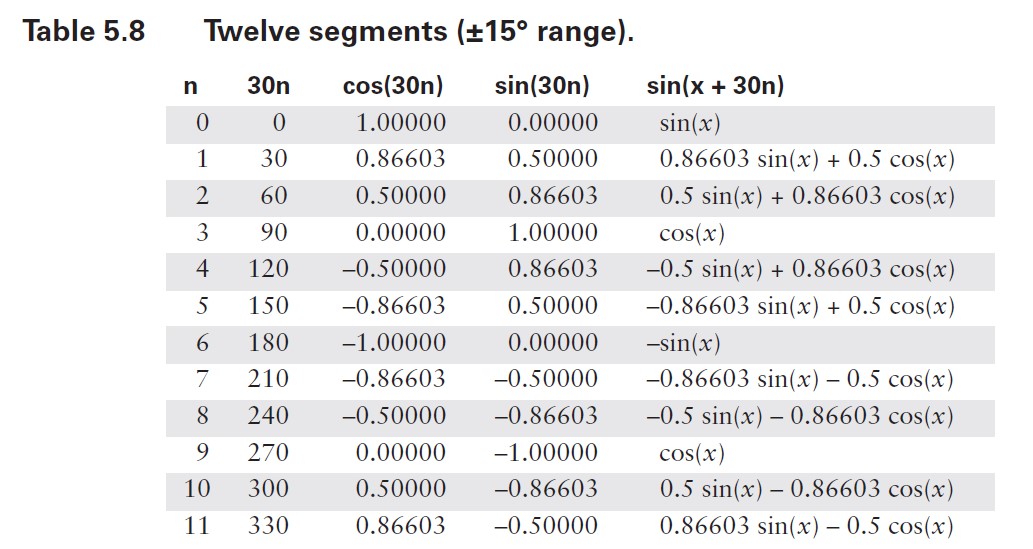
在许多场景下（例如坐标旋转），需要用到同一个角度的正弦值和余弦值。如果此时已经为计算正弦值而对约简后的角度同时计算了两个三角函数值，那么余弦值几乎是 “顺带免费” 得到的。在这种情况下，使用更小的角度范围就非常有意义。此外，通过限制角度范围，级数展开所需的项数可以更少。清单 5.5 展示了一个基于表 5.8（15° 范围）的超快速单精度浮点实现。需要注意的是，对于这个角度范围和精度要求，正弦级数可以简化为三项，余弦级数简化为四项，这两个表达式因此会呈现非常简单的形式。

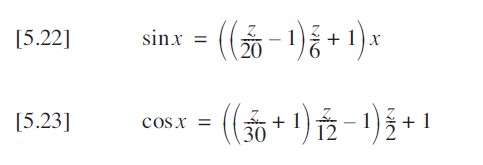
这看起来开始简单多了。由于这些函数非常简短，我甚至可以通过将它们作为内联函数插入来进一步加快速度。

Listing 5.5 Both at once.
// Find both the sine and cosine of an angle
void sincos(double x, double *s, double *c){double s1, c1;long n = (long)(x/pi_over_six + 0.5);x -= (double)n * pi_over_six;n = n % 12;if(n < 0)n += 12;double z = x*x;double s1 = ((z/20.0-1.0)*z/6.0+1.0)*x;double c1 = ((z/30.0+1.0)*z/12.0-1.0)*z/2.0+1.0;switch(n){case 0:s = s1;c = c1;break;case 1:s = cos_30 * s1 + sin_30 * c1;c = -sin_30 * s1 + cos_30 * c1;break;case 2:s = sin_30 * s1 + cos_30 * c1;c = -cos_30 * s1 + sin_30 * c1;break;case 3:s = c1;c = -s1;break;case 4:s = -sin_30 * s1 + cos_30 * c1;c = -cos_30 * s1 - sin_30 * c1;break;case 5:s = -cos_30 * s1 + sin_30 * c1;c = -sin_30 * s1 - cos_30 * c1;break;case 6:s = -s1;c = -c1;break;case 7:s = -cos_30 * s1 - sin_30 * c1;c = sin_30 * s1 - cos_30 * c1;break;case 8:s = -sin_30 * s1 - cos_30 * c1;c = cos_30 * s1 - sin_30 * c1;break;case 9:s = -c1;c = s1;break;case 10:s = sin_30 * s1 - cos_30 * c1;c = cos_30 * s1 + sin_30 * c1;break;case 11:s = cos_30 * s1 - sin_30 * c1;c = sin_30 * s1 + cos_30 * c1;break;}
}

如果划分为更小的角度可以按照如下方式进行：

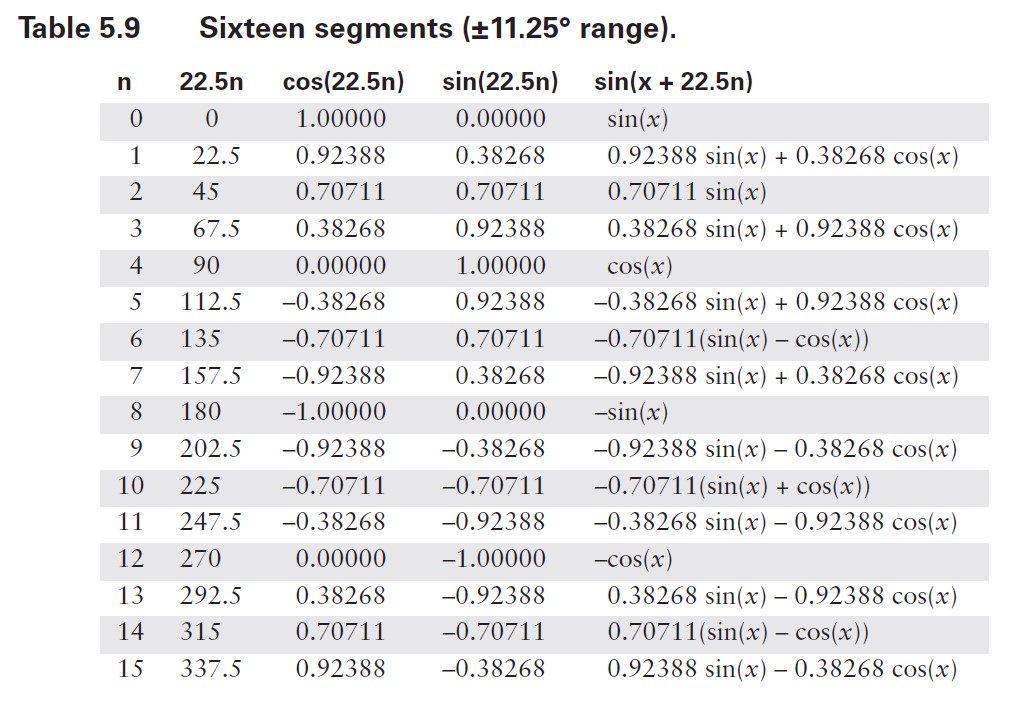
一篇关于正弦和余弦的文章若不提及切比雪夫多项式的应用，就不算完整。从根本上讲，切比雪夫多项式理论允许程序员对系数进行微调，以实现整体误差上限的降低。当截断一个多项式时，通常在 x 较小时误差非常小，但在 x=0 附近的某个范围外，误差会呈指数级急剧增大。另一方面，切比雪夫多项式围绕零值振荡，其峰值偏差有界且相等。用切比雪夫多项式表示幂级数，可使你用零点附近的微小误差换取自变量范围极值附近小得多的误差。在此我不会详述切比雪夫多项式理论，目前仅给出该过程的结果。

就本讨论而言，你无需了解具体实现方式，但总体思路是：用切比雪夫多项式的等价形式替换 x 的每一次幂，合并同类项，按该形式截断级数，再替换回原形式。当所有项合并后，你会发现其又回到了 x 的幂级数形式，但系数已以最优方式略微调整。由于该过程可降低最大误差，通常会发现你能在级数展开中减少一项左右，同时仍保持相同精度。