【Fifty Project - D26】

间歇性螺旋式懈怠了好多天，不过只是懈怠了记录，每天还是按时超量完成学习、作息、锻炼。连轴转了几天搞定了答辩，接下来还有一系列答辩材料和毕业材料要准备QAQ

今日完成记录

Time	Plan	完成情况
9：00 - 10：00	答辩记录等文件编写	√
11：00 - 13 ：00	Leetcode	√
13：30 - 14：30	有氧	√
19：00 - 19：30	《新参者》	√

Leetcode

单调队列

停止记录的几天结束了栈的题单，队列的题单也逐渐来到末尾，最后几个单调队列的题，尤其是这个和至少为K的子数组，实在煎熬。

单调队列：即保存数据单调上升或者单调下降的队列。题目中一般结合滑动窗口和双端队列实现，几个题都是hard，虽然可能没有那么hard，主要还是考验对单调队列的理解和应用。慢慢撕出来可以显著加深对单调队列的理解。

预算内的最多机器人数目：两个数组，一个是充电时间数组chargeTime，一个是费用数组runningCost，表示了n个机器人的充电时间以及各自的运行费用，现要求在允许的最大费用k内选定连续的一批机器人，返回能选定的最大机器人数量。费用计算公式为$cost=max(chargeTim{e}_i)+sum(runningCos{t}_i)$。
思路：观察费用公式可知，需要维护滑动窗口内两个统计量，一个是最大值，一个是总和。然后求最大滑动窗口。观察公式还可以知道：当滑动窗口左侧固定，右侧入队只会增大费用，当右侧固定，左侧出队必然会降低费用。因此先贪心一直扩大窗口大小，直到费用溢出，期间更新合法结果，溢出后左边持续出队直到费用再次合法，依照上述流程滑动窗口，最终得到最大长度。
还需要考虑如何计算费用：总和是容易计算的，一个变量即可。但是要如何计算滑动窗口的最大值呢？有两个方法：1.用堆记录所有窗口划过的值，用map记录每个值出现次数，当出窗口时更新map的次数，每次读堆的最大值都判断一下map中记录的次数是否为0；2.利用单调队列记录。

详细解释一下单调队列的思路

首先，我们先不引入单调队列，而是简单地使用一个队列去保存所有可能成为最大值的数，并且讨论一下随着滑动窗口扩张和收缩，这个队列中保存的数的情况以及最大值变更的情况如下：
1） 扩张滑动窗口
如图1当滑动窗口包括11，那么毋庸置疑的最大值是11

如图2，当滑动窗口扩张到4，窗口内有11和4，那么如果11出队，4必然是新的最大值，因此可能成为最大值的数队列此时是（11， 4）【意思是当前最大值为11，如果当前最大值出队了，那么新的最大值是4】

如图3，当滑动窗口继续扩张到7，此时滑动窗口内是（11，4， 7），可见当11出队，新的最大值应该是7，所以此时的最大值队列应该是（11， 7）。【最大值是11，但是如果11出队，最大值是7】
可见4已经失去了候选权，因为我们的滑动窗口是从左往右的，也就是4必然在7之前出队，而只要7在队中那么4就不可能当上最大值，所以队列中应该保存（11，7）

如图4，滑动窗口继续扩张到14，此时滑动窗口内是（11，4，7，14），可见最大值应该是14了，因此队列中的（11， 7）都得出队，因为只要14在一天，11和7就永无出头之日，且11和7在14的左边，也就是必然先出队，可见11和7已经不可能成为最大值了。

如图5继续扩张0，当滑动窗口扩张到（11，4，7，14，10，9，8）时，备选的最大值队列应该是（14，10，9，8）

2）左边收缩滑动窗口
图6展示了当图5窗口左侧收缩，依次出队11、4、7后，两个队列的情况，最大值队列不变，因为14没有出队。

当14退出滑动窗口，最大值队列同样退出14，10将成为新的滑动窗口最大值。如下图

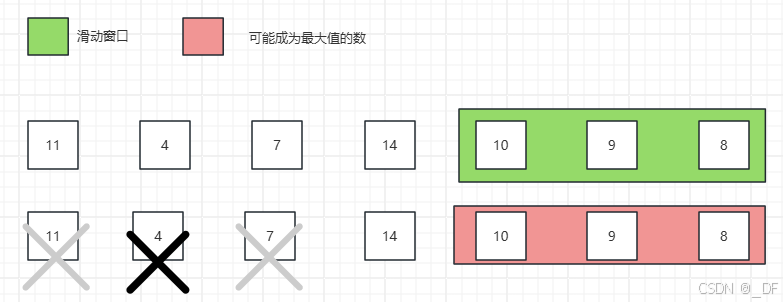
从上面的扩张和收缩过程，可见最大值数组可以用单调队列完美实现。

和至少为K的最短子数组：给定一个数组arr和一个K，要求返回和至少为K的最短子数组的长度。数组中的数可能出现负数，K是大于0的正整数。
思路：因为数组中会出现负数，所以直接使用滑动窗口就不适用了，无法判断什么时候要收缩窗口。因此考虑使用前缀和辅助，首先计算数组的前缀和数组，核心问题在于决定什么时候需要收缩窗口：（1）当前子数组和不足K，需要收缩窗口得到更大的和（移除左侧一些和为非正数的子数组）（2）当前子数组和大于等于K，通过收缩窗口看是否能使用更小的子数组满足题干要求。
第二个情况很好解决，直接收缩同时判断当前和是否大于等于K即可。第一个情况困难点在于你需要知道每次收缩需要收缩到什么地方，也就是找到这个和为非正数的前缀子数组。

如上图，两个绿色框中的子数组都属于和为非正数的子数组，以他们为前缀的话对寻找目标和大于等于K的最短子数组是没有作用的，第一个框和为0，所以后续的数组如果满足和大于等于K，加上这个子数组只会更长，与目标不符；第二个框和为-3，后续数组加上这个前缀会使得和更小（增加了长度但是减小了和）这也与目标相悖。因此在遇到这种子数组的时候需要从左侧排出（不能以这些数组为首）
将这个数组符号化为bad_arr，长度为j，下标是start, end。当我们发现滑动窗口左侧是start的时候，应该直接将窗口收缩到end+1，这也就是上面说的遇到这个子数组就得从左侧排出的做法，接下来我们需要观察这些数组的特性以得到一种快速记忆start和end的方法。
观察这些数组可以发现几个特点：
（1）pre[end] <= pre[start - 1]，因为这些数的和是小于等于0的，所以尾部前缀和必然小于等于首部-1的前缀和。
（2）这类子数组是可合并的，如下图，两个绿色合并后的红色区域子数组和是-3，

结合上面两个特点，我们可以使用一个单调队列记忆前缀和，最开始是0，然后记忆所有小于单调队列队尾的点，每次要收缩的过程，如果收缩节点下标是单调队列的队头，则让对头出队，再收缩到单调队列的新队头。

单调队列太难了QAQ，理清楚这个逻辑太难了

《新参者》

结束了《挪》后一直没有找新的书，一方面是抽屉里还有三本朋友送的东野圭吾，一方面是不太喜欢去图书馆，去一趟借书回来会让我感觉投入成本有点高hhhh，就是拿回来的书不看完感觉很亏，但是又决定不好选什么书。

之所以又一直没有开始东野圭吾，是因为想着总得阅读点有内容深度的东西吧（没有diss东野圭吾的意思哈），感觉侦探小说更多在于推理消遣，而不是那种类型的小说（看了以后会让自己思考的东西）

最后又开始了《新参者》是因为想着饭后刷抖音还不如看会侦探小说了hhh.

那么就开始加贺侦探的新参者啦

看完了第一章，不愧是以温情出名的《新参者》，第一章的小故事以嫌疑人保险哥带出了调查的案件，保险哥因为和仙贝哥的约定，编造了自己的行踪，给自己招上了嫌疑人的锅，不过加贺老哥敏锐的观察力（真的牛蛙）解释清楚了，实际上是因为仙贝哥为了向母亲隐瞒母亲自己的病情跟保险哥通了气，自己给保险哥真的病历提交保险材料，再跑一趟去找老太太拿伪造病历材料，导致了时间线上出现了三十分钟误差。