强化学习《初学者》--基础概念贝尔曼公式
强化学习(Reinforcement Learning, RL)是机器学习的一个重要分支,它专注于让智能体(Agent)通过与环境(Environment)的交互来学习如何做出最优决策。

可能会觉得有些抽象,想象一下训练小狗做动作:如果它做对了,你就给零食(奖励);做错了就不给甚至轻微惩罚。
强化学习的最终目标:求解最优策略。沿着这个最优策略可以最大化长期累积奖励,而不是单次奖励。
一、基础概念
整篇会以网格寻找到目标网格的最优路径为例:

任务:从开始网格,找到到达目标网格的最优的路径。
1.1 状态(State)
智能体相对于环境的状态(如游戏画面、机器人传感器数据)
对于这个例子来说,这个状态可以是位置,总共有9个状态:

状态空间可以表示为:
对于更复杂的状态可以包括速度、加速度等,具体的状态所包括的变量取决于当前的任务。对于例子的这个任务来说,只需要关注于位置即可,所以状态时位置。比如机器人的状态可以有位置、速度、加速度等等。
1.2 动作(Action)
对于每个状态,智能体可执行的操作
对于这个例子来说,对于每个状态,可能执行的动作有五个:向上、向右、向下、向左以及保持不动,分别表示为、
、
、
以及
。

每个状态的动作空间可以表示为:
不同的状态可以有不同的动作空间。
1.3 状态转移(State transition)
当采取动作时,智能体的状态可能会发生转移,从一个状态转到另一个状态,这个过程就成为状态转移。
例如,对于状态,选择动作
时,则转移到状态
:
对于状态,选择动作
时,则转移到状态
:因为
往上之后没有表格了
状态转移可以看作智能体和环境的一种交互行为。
状态转移的表格表示:

对于表格的表示来说,它只能表达确定的状态。
也可以使用概率来表示状态转移,其实就是使用条件概率来表示:在状态,如果选择动作
,则状态转移到
:
概率表示也是确定性的情况,但是状态转移可以是随机的,可以根据概率,随机选择一条状态来进行转移。
1.4 策略(Policy)
智能体决定动作的规则(如“在状态A时选择动作B”)。告诉智能体要选择哪一个状态
直观的表示:箭头表示策略

基于这个策略,从不同的点出发,则可以得到不同的路径:

数学表征为:同样使用条件概率
这是一个确定的策略,也可以有不确定的策略:

表格表征:

1.5 奖励(Reward)
环境对动作的即时反馈(如得分增加、能量消耗),也就是采取某个动作之后的得分,是一个实数、标量,可以看作人机交互的手段,引导智能体按照我们期望的方式行动。
分为:
- 积极奖励:鼓励这种行为(0奖励也算一种特殊的鼓励 )
- 消极奖励:乘法这种行为
在例子当中,可以设置一下奖励规则:
- 智能体尝试越出边界:
- 智能体进入forbidden cell:
- 智能体进入目标cell:
- 其他:
表格表征:

表示的是确定性的情况。
数学表征:条件概率,在状态时,如果我们选择动作
,奖励是-1。
- 在
和
的条件下,
的概率为1,其他条件下
的概率为0
注意:
- 奖励规则是确定的,但是奖励转移时随机的。只有学习了就有奖励,但是获得奖励是 不确定的。
- 奖励依赖于当前的状态和动作,而不是下一个状态。
1.6 trajectory(轨迹)和return(回报)
轨迹是一个 “状态-动作-奖励”链:
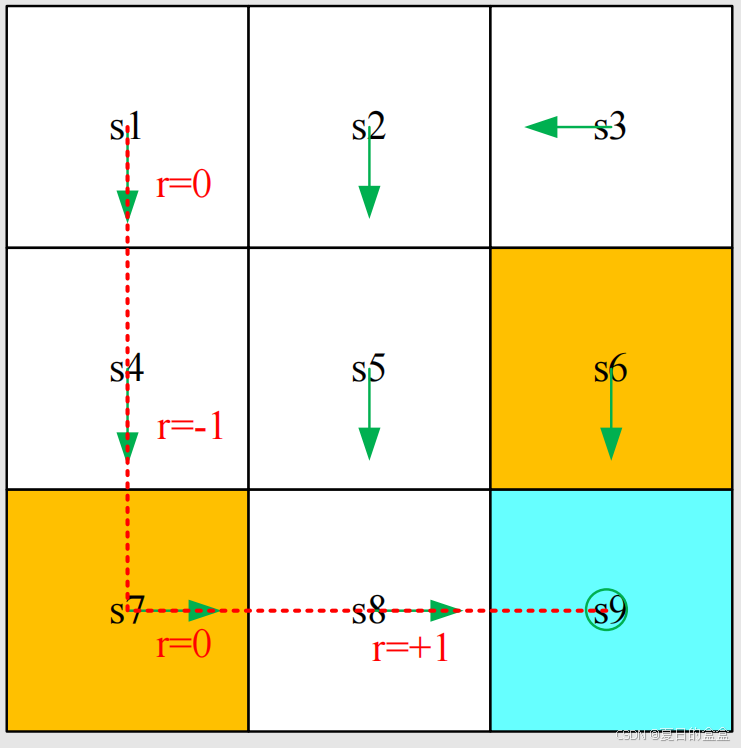
回报的即是当前路径的奖励 :
判断哪个策略比较好:可以哪个策略的回报是greater。回报可以判断策略的好坏。

上面的第一个策略的轨迹可以表示为:

回报为:
这个回报是没有意义的,因为这个回报时发散的。这个时候就需要discount rate,discounted return:
通过的控制,回报就变成有限的,并且可以平衡短视和长视奖励,也就是是说:
- 如果
接近于0,discounted return的价值主要是近期获得的回报。
- 如果
接近于1,discounted return的价值主要是长期获得的回报。
1.7 Episode
当智能体遵循某个策略与环境交互时,可能会在某些终止状态处停止。由此产生的状态-动作序列被称为一个Episode。

一个episode通常被定义为一段有限的交互轨迹。包含这类有限episode的任务称为episodic tasks。
有的任务没有终端状态,意味这与环境的交互没有结束点,这类任务称为持续任务(continuing tasks)。
实际上,我们可以通过将分集任务(episodic tasks)转化为持续任务(continuing tasks),在统一的数学框架下对待这两类任务。
- 方案1:将目标状态视为一种特殊的吸收态。一旦智能体进入了吸收态,它便永远不会离开。从此时起,后续的奖励均为 r = 0。
- 方案2:将目标状态视为一个正常的、具有策略的状态。即使智能体到达了目标状态,也可以选择离开。每次进入目标状态时,将获得 r = +1 的奖励。
这篇文章里面采用了 方案 2,这样做的好处是无需将目标状态与其他状态区别对待,可以像处理普通状态一样来处理目标状态。
1.8 马尔可夫决策过程(MDP)
MDP的主要元素:
集合:
- 状态
- 动作
- 奖励:
概率分布:
- 状态转移概率:在状态s,采取动作a,转移到状态s'的概率为
- 奖励概率:在状态s,采取动作a,获得r奖励的概率为
策略:在状态s,选择动作a的概率为
马尔可夫属性:无记忆性属性
在马尔可夫过程中,未来的发展只依赖于前一个状态,而与过去的历史无关。
则网格这个例子也可表示为更加通用的模型:马尔可夫过程

圆圈表示状态,带有箭头的链接表示状态转移。
一旦给出策略,马尔可夫决策过程就变成了马尔可夫过程!
1.9 总结

强化学习就是智能体根据当前的状态选择动作,之后在环境中会进入另一个状态并获得一定的奖励,通过多次迭代,最大化这个累计奖励。
强化学习是一种机器学习方法,与监督学习和无监督学习不同。它并不依赖于标注数据,而是在一个环境中通过试错来学习最佳策略。这类似于小孩子通过尝试不同的行为来学习正确的做法。在强化学习中,核心要素:
- 状态:智能体相对于环境的状态(如游戏画面、机器人传感器数据)
- 动作:对于每个状态,智能体可执行的操作
- 奖励:环境对动作的即时反馈(如得分增加、能量消耗)
- 策略:智能体决定动作的规则(如“在状态A时选择动作B”)
- 状态转移:当采取动作时,智能体的状态可能会发生转移,从一个状态转到另一个状态,这个过程就成为状态转移。
二、贝尔曼公式
2.1 回顾return
回顾之前的内容,说过Return可以反映策略的好坏:下面三个路径通过计算可知第一个轨迹是最好的,第二个最差,第三个可能好也可能差,有一定的概率

- 第三个不是传统意义上的return,而是return的平均值
2.2 计算return
方法1:通过定义,表示从
出发得到的return

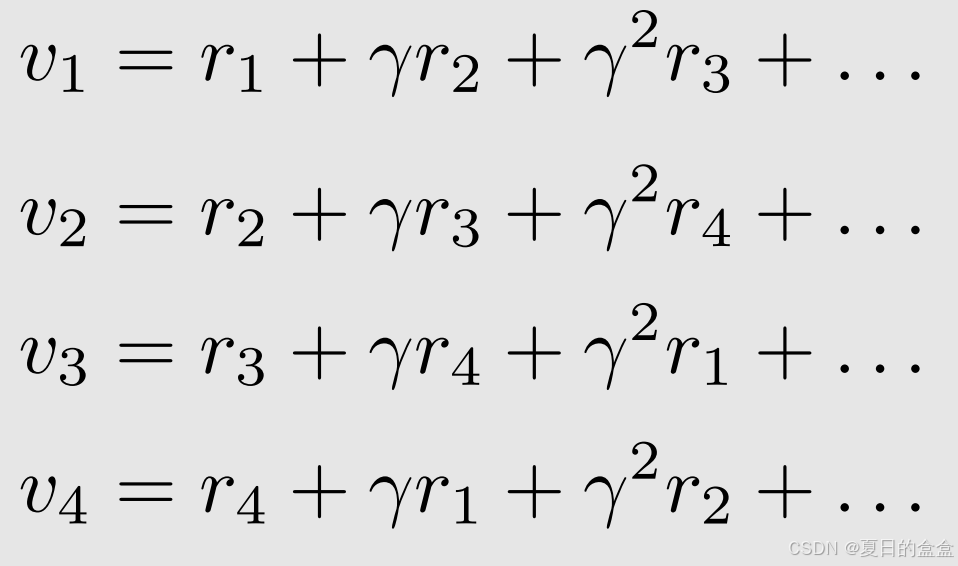
方法2:推导,状态之间的return存在依赖性 ,称为Bootstrapping。当前return依赖于其他的return

可以将上面的公式写成矩阵的形式:

也就是:特定确定性问题的贝尔曼公式
P矩阵就是策略(在这个例子里面,比较简单),通过这个公式可以求解v
以下的例子就可以直接写出来return的依赖性:


2.3 state value
首先考虑单步的情况,状态经过动作
会转移到状态
,并得到奖励
:
在这里面,动作、奖励、状态都是由概率决定的,具体而言:
- 策略决定动作:也就是
由
决定
- 状态和动作决定奖励:也就是
由
决定
- 状态和动作决定状态转移:也就是
由
决定
考虑多步的轨迹:
discounted return是:
是discounted rate
state value就是的期望(期望值/平均值):也叫state-value function
- 它是s的函数。它是一个条件期望,条件是状态从s开始。它是s的函数。它是一个条件期望,条件是状态从s开始。
- 它基于策略π。对于不同的策略,state value可能不同。
- 它代表状态的“值”。如果state value越大,则策略越好,因为可以获得更大的累积奖励。
return和state value的区别:
- state value是从一个状态开始可以得到的所有可能的return的平均值。如果π(a|s), p(r|s, a), p(s'|s,a)都是确定性的,则state value与return值相同。
有如下三个策略:


相较于2.1的return来说,和
是一致的,因为是确定性的,而对于
来说只能计算state value,因为是不确定的。
2.4 贝尔曼公式(Bellman equation)
state value可以衡量策略的好坏,这是很重要的,但是要如何计算呢?使用到的就是贝尔曼公式。
Bellman equation:描述不同状态的state value之间的关系
考虑随机的轨迹:
返回的:
即时奖励
未来奖励
state value定义为:
将期望值拆开进行分析,对于第一个期望值:对于每一个状态,根据策略有不同的动作可以选择,第一个期望值也就是即时的奖励

- 选择动作a的概率是
,对应的state value是
。
- 在s和a情况下,奖励为r的概率为
,故
为
对于第二个期望值:从当前状态出发所得到的下一个时刻的return,也就是未来奖励的期望值:
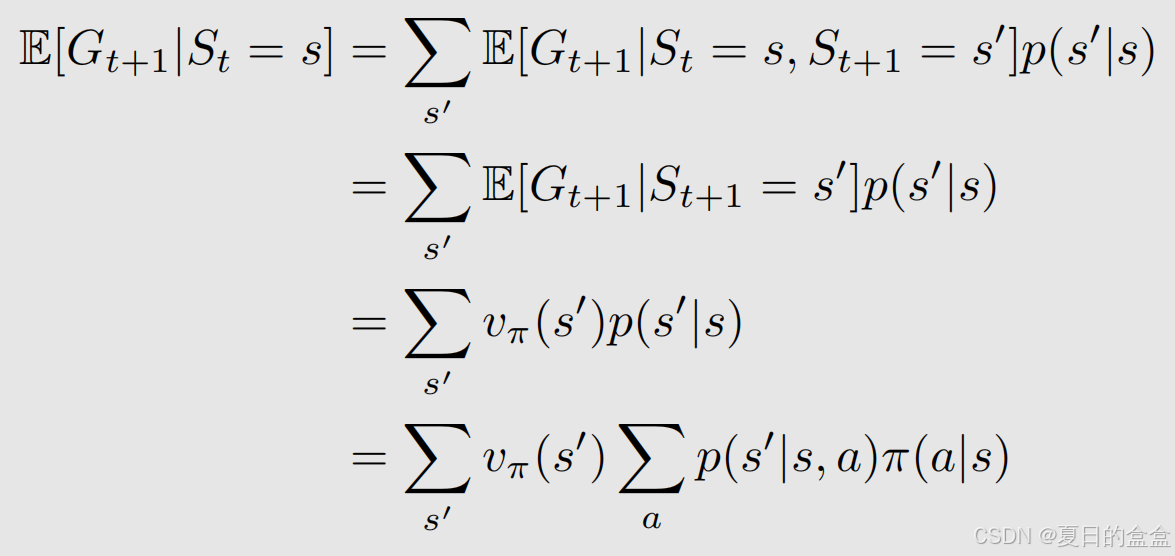
- 因为马尔可夫无记忆性,
由上可得贝尔曼公式:

- 描述不同状态的state value之间的关系,也就是
和
的关系
- 包含两项,第一项是即时奖励、第二项是未来奖励
- 每个状态都满足这个公式
和
是状态值,可以计算的,存在依赖性,也就是Bootstrapping
是既定的策略,求解这个公式也称为策略评估
和
表示动态模型,也分为model-based和model-free
如下例子:

根据贝尔曼公式可知需要计算如下的参数:
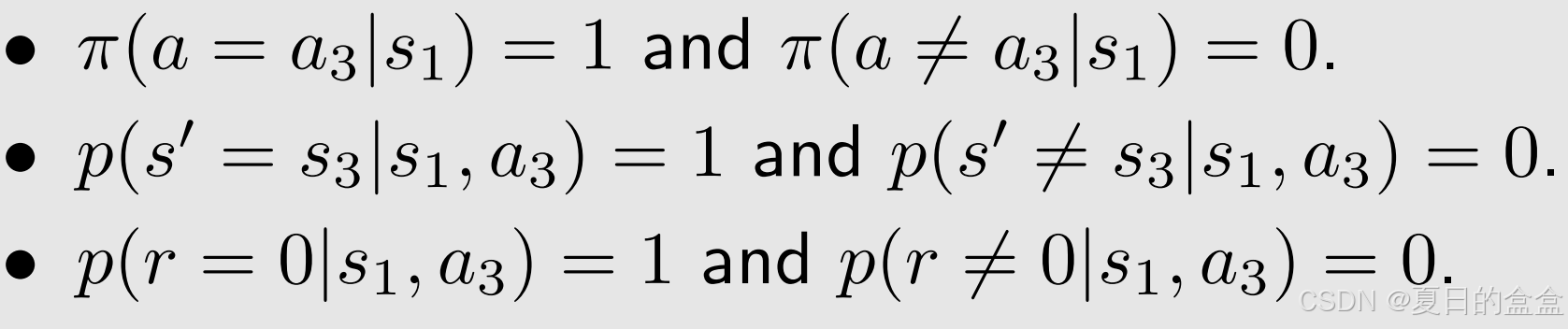
代入参数计算state value:
![]()
直观的理解,state value=即时奖励+未来奖励,故
![]()
同样的方法可以写出其他状态的state value:

求解:

如果:所以
的加载高于
(直观来说,
比
离目标点近)

计算出state value之后就可以改进这个策略
介绍更复杂的例子:

计算每个状态的state value:

求解state value:

如果:

比较两个例子,这个例子state value小于前一个例子,故可以得出结论,前一个策略会比较好。

2.5 贝尔曼公式的矩阵形式
为什么要介绍矩阵形式:可以帮助求解贝尔曼公式。

重构贝尔曼公式:
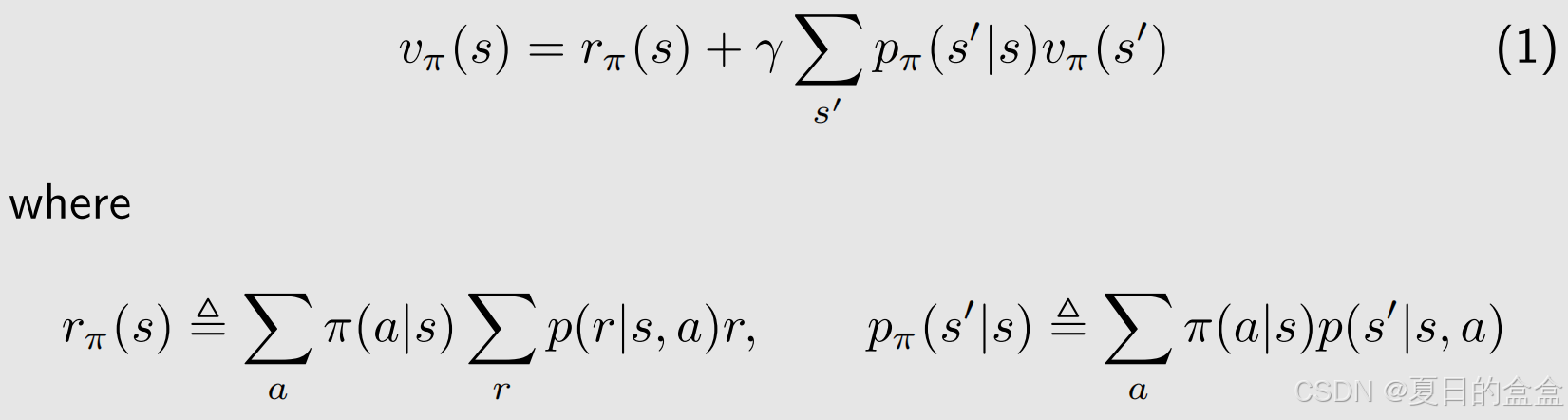
代表即时奖励的平均值,
对于多个状态:i=1,2,...,n
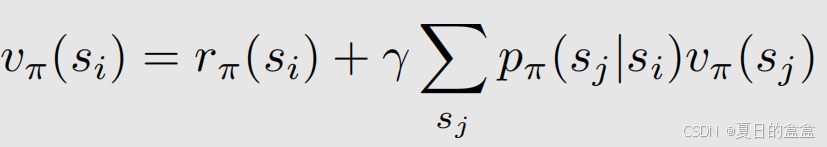
转换为矩阵形式:

其中:

是二元矩阵,状态转移矩阵(是概率值),
代表即时奖励,
需要求解的state value
 举例进行说明:总共四个状态
举例进行说明:总共四个状态

给出矩阵的环境和策略如下:

贝尔曼的矩阵表达式如下:

例子2:不确定性策略

直接代入公式:

2.6 求解state value
为什么要求解:策略评估:给定一个策略,找出相应的state value称为策略评估
- 给出策略
- 列出贝尔曼公式
- 求解贝尔曼公式
方法 1:公式法

这种方法需要利用工具计算逆矩阵,比较麻烦
方法2:迭代法
![]()
迭代计算出,可以证明出:
![]()
举例进行说明:首先是两个比较好的策略,


通过计算,两个策略最后计算出来的state value值一致,说明不同的策略,state value可能一样
比较两个不好的策略:


2.7 action value
- state value:智能体从一个状态开始可以得到的平均return。
- action value:智能体从一个状态开始并采取一个动作所能得到的平均return。
为什么要关注action value:因为可以知道哪个动作 (action)更好

- 是一个状态-动作对(s,a)函数
- 依赖于策略
state value和action value的关系:在一系列动作里面选择a的概率是,值是

即:已知action value和策略,可以计算出state value

将这个公式和前面的贝尔曼公式相比:

可以得到:即时奖励+未来奖励

故计算出每个状态的state value以及已知的每个动作的概率值和奖励,即可计算出每个状态的每个动作的action value。
举例进行说明:

写出状态1的action value:只会有动作

注意:其他动作的action value并不为0,只是当前的策略没有其他动作,但并不代表其他动作没有value,如果当前策略的当前动作不行,下一次就需要尝试其他动作。
其他动作也需要进行计算:

- 动作值很重要,因为我们关心采取哪个动作。
- 我们可以先计算所有状态值,然后计算动作值。
- 我们也可以直接计算有或没有模型的动作值。
2.8 总结
两个关键性概念:
- state value就是在s状态
的期望(期望值/平均值),可以用它衡量策略的好坏

- action value就是状态s下选择动作a
的期望(期望值/平均值,可以知道哪个动作 (action)更好

- 它们之间的关系


贝尔曼公式:描述不同状态的state value之间的关系

贝尔曼公式的矩阵表达:可以求解state value

求解贝尔曼公式的两种方法:
- 公式法
- 迭代法
三、优化策略和贝尔曼最优公式
章节重点:
- 核心概念:optimal state value and optimal policy
- 基础工具:the Bellman optimality equation (BOE)
回顾之前的内容:

由上面的state value可以计算出action value:

介绍state value的时候提到了,state value可以衡量策略的好坏,当策略不好的时候,我们可以怎么改进它?答案是使用action value来改进策略
当前策略是:

但当我们计算action value的时候,的值不是最大的,而是
:

优化的方式是选择action value最大的动作,也就是。
新的策略可以定义如下:

持续更新……
参考:B站up主第1课-基本概念(State,action,policy等)_哔哩哔哩_bilibili,听视频时做的笔记。
