算法-贪婪算法
贪婪算法
可行解:满足条件约束的方案,有多个
最优解:满足问题的目标,只有一个,最好的方案
优化问题:一个问题需要最小或最大的结果(即需要找到最优解)
贪婪算法:用于解决优化问题,分阶段解决
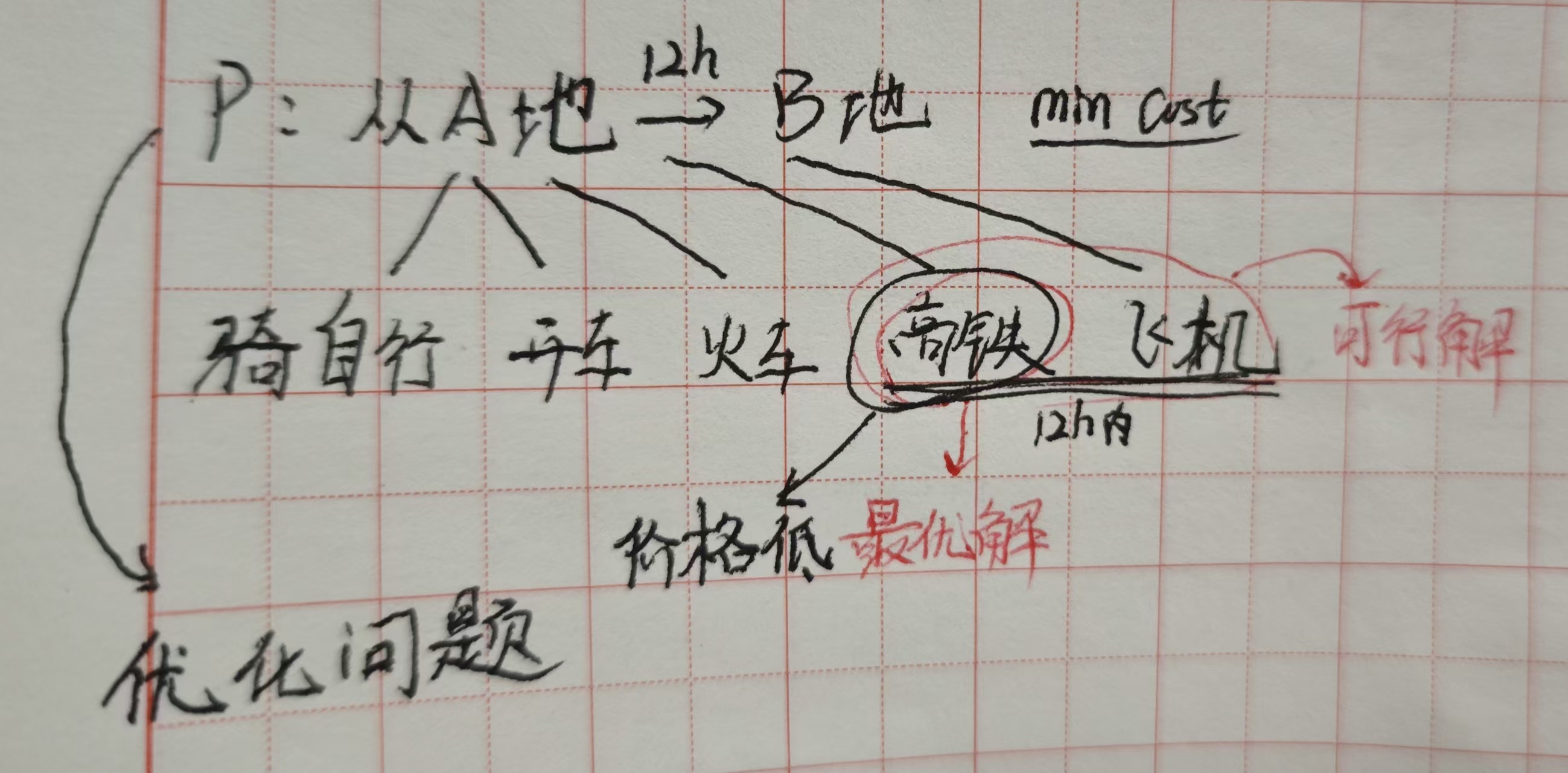
//a是一些输入,n是a的大小。进行遍历筛选a,a是可行的就包含在解决方案中。
Algorithm Greedy(a,n){for i=1 to n do{x=select(a);if feasible(x) thensolution=solution+x;}
}
实景举例:假如你要选择一款功能性最好的车。不必去所有店里,看所有的车,这将是浪费时间的。你可以从品牌,上线时间,硬件情况,买的人数等等条件筛选出了几款,然后再找出最好的那一台。
再假如要招员工,1000选1,需要简历,测试,技术面试,小组讨论,人力面试等等,非常麻烦。选择一种最好的方式来筛选。
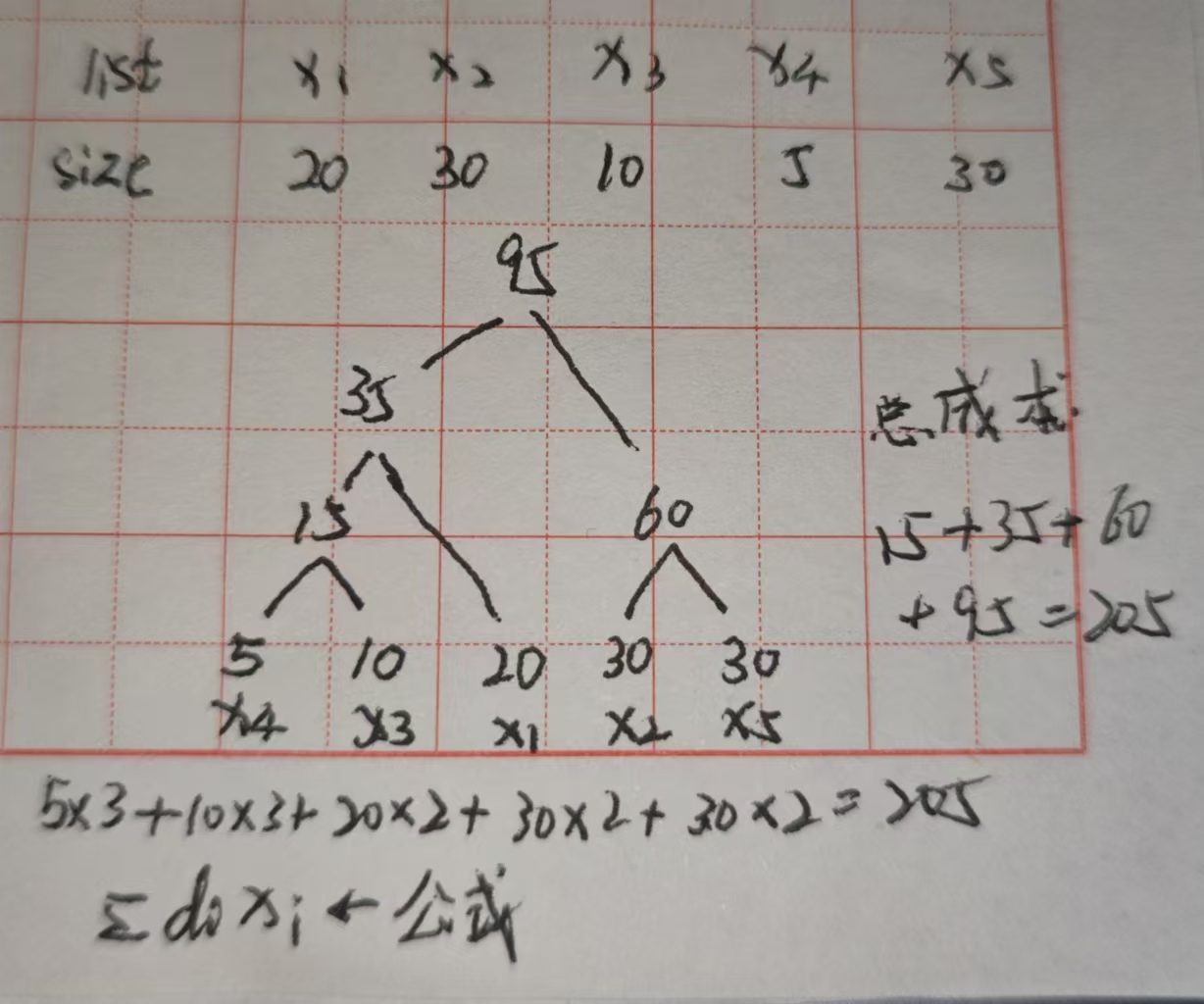
背包问题
袋子容量m,物体数量n。运输蔬菜,最好的方式装满,以获得最大利润
分阶段:选择输入(最好的方式)–验证是否满足条件–验证是否达到目标

带截至时间的作业调度
背包问题物体是可分割的,而作业调度不可分割。
注意:每个工作只需要一个单位,所以可以选择3个工作。因为没有人愿意等待工作,所以只可以选择3个工作。

最优合并模式
多个列表合并排序,先合并小列表,时间复杂度会更小些。
霍夫曼编码
一种压缩算法,就像文件一般通过压缩包进行传输以减小文件大小 。
非固定大小的编码:字母数量多的编码位数少,自然就小了。
自行构建编码的话,需要解码所以代码图表也要传输的,总位数就是msg+table。

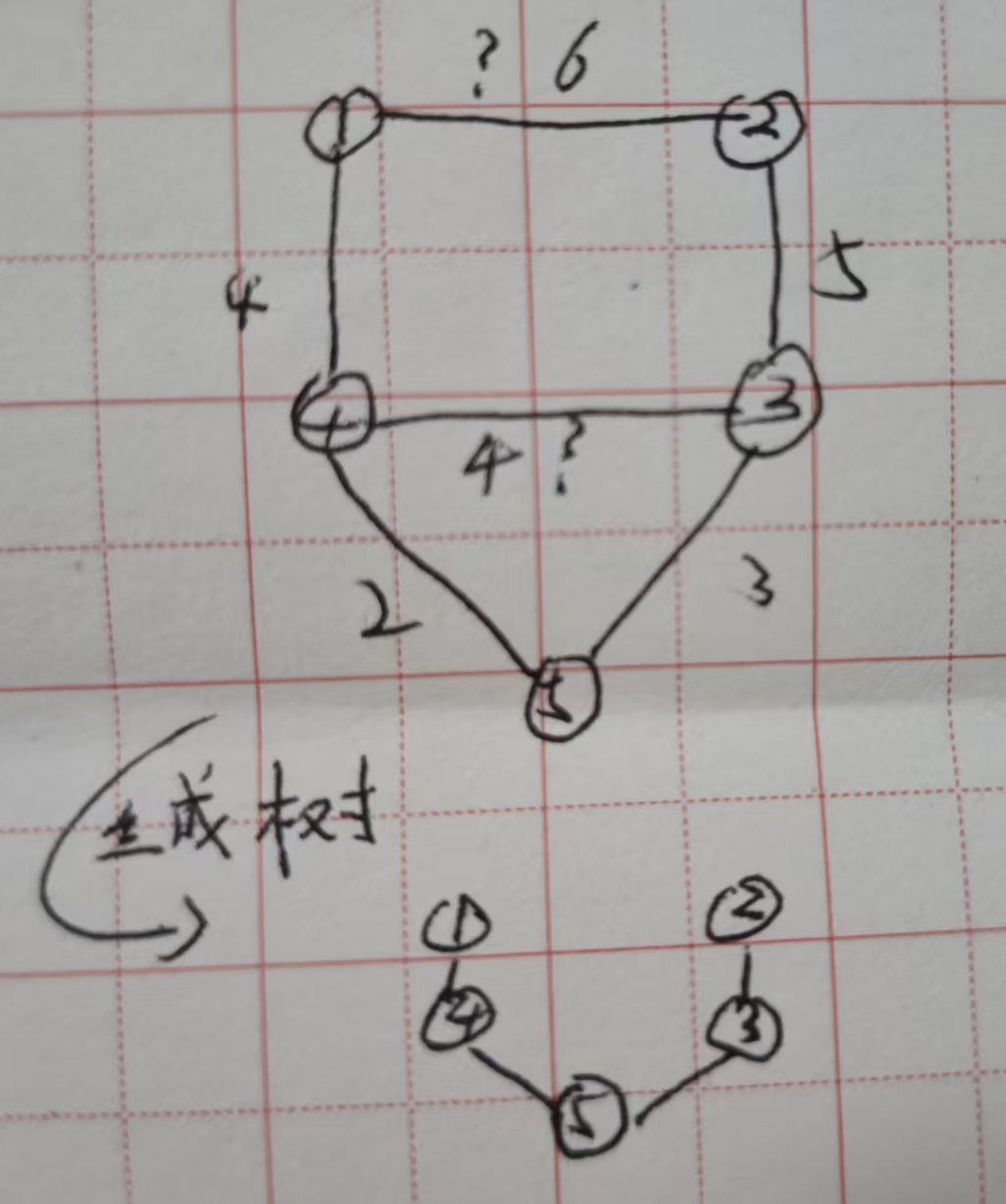
Prim算法和kruskal算法(连通图)
算法是为了找到最小生成树,即最优解。
1.生成树:无向连通图的子图,包含所有顶点,顶点-1为边数,不会形成循环,就是生成树。
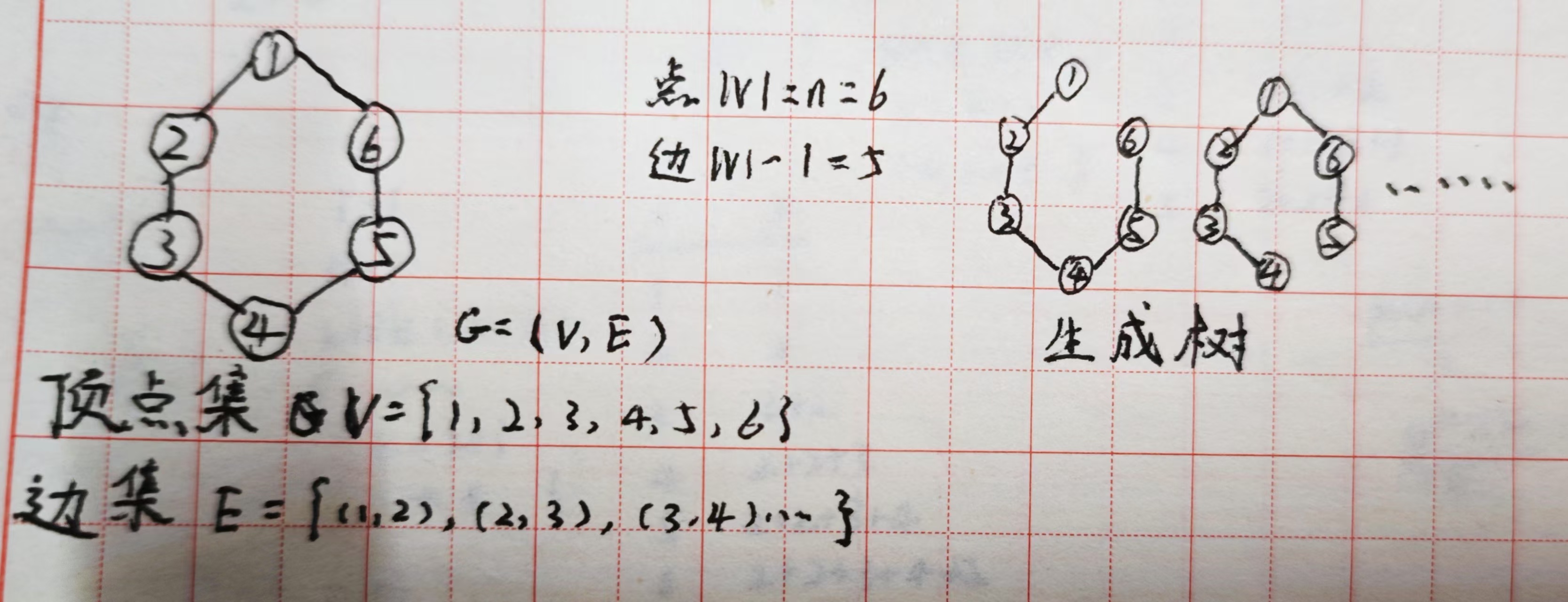 2.prim算法:他认为先选择权重最小的一条边作为基准边,之后持续选择小边,但要保证之后选的边要与已选的顶点相连(即保证连通)。
2.prim算法:他认为先选择权重最小的一条边作为基准边,之后持续选择小边,但要保证之后选的边要与已选的顶点相连(即保证连通)。
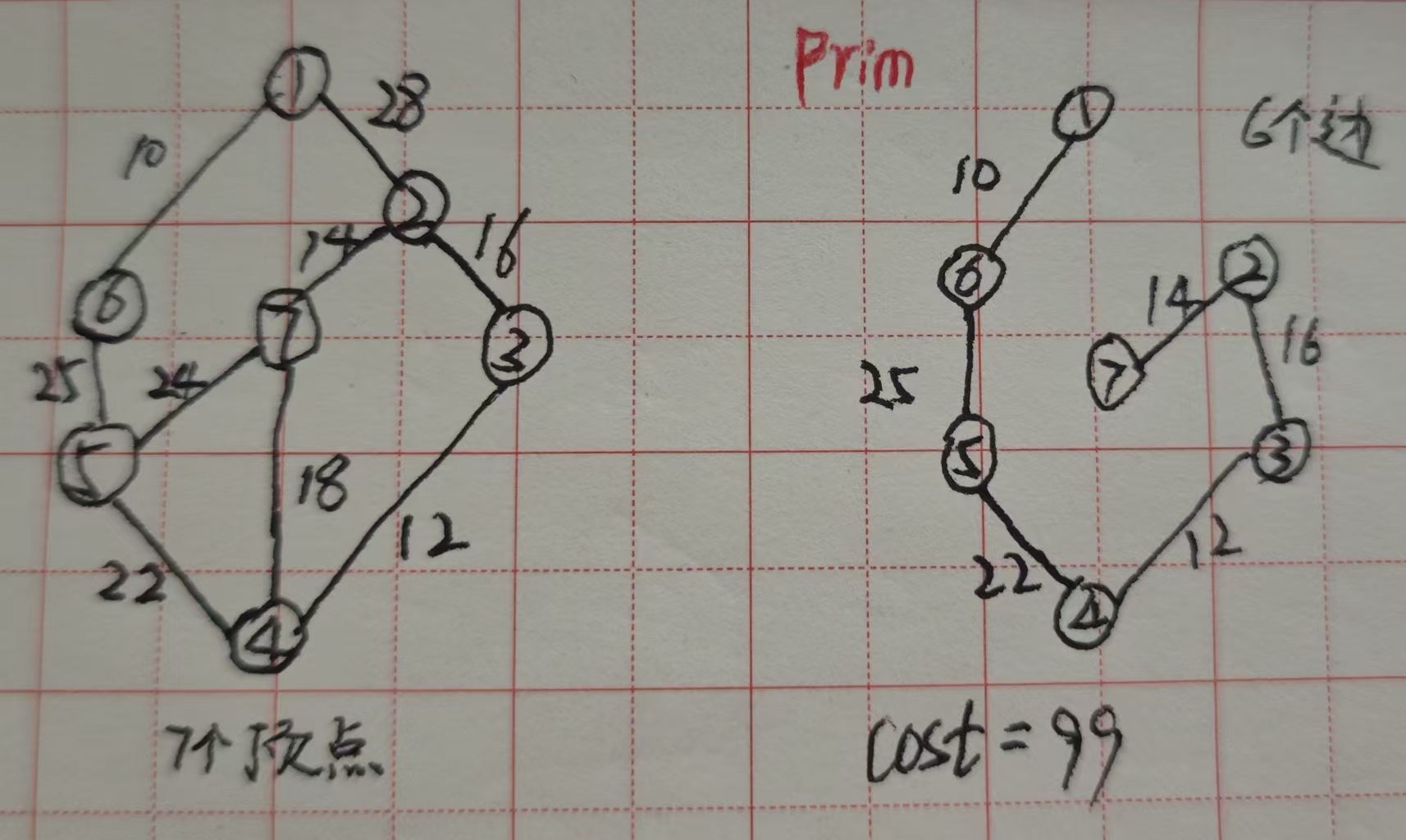
3.kruskal算法:他认为要一直选择权重最小的一条边,但是如果要形成循环就弃掉此边。
还用上面的例子发现通过kruskal找出的最小生成树和prim一样。
时间复杂度:先找到边,然后要找到多少条边,即O(VXE)=O(n2),因为始终要选择最小边,那么如果采用最小堆,时间复杂度将是O(nlogn)。
算法还可以解决知道最小生成树求权重问题:
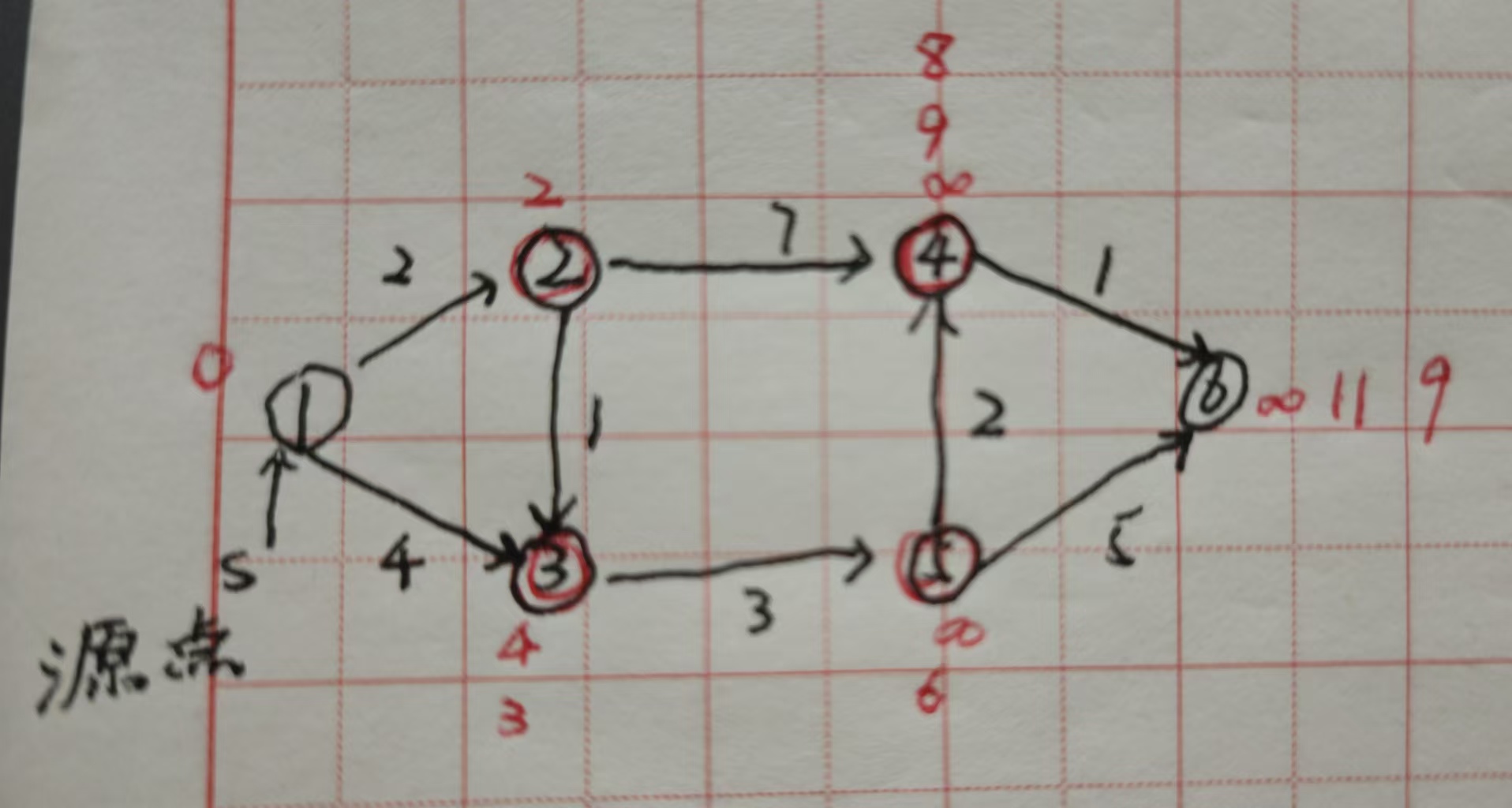
Dijkstra算法-单源最短路径
1.它可以在有向或无向图中,找到从单个源点到其他顶点的最短路径。
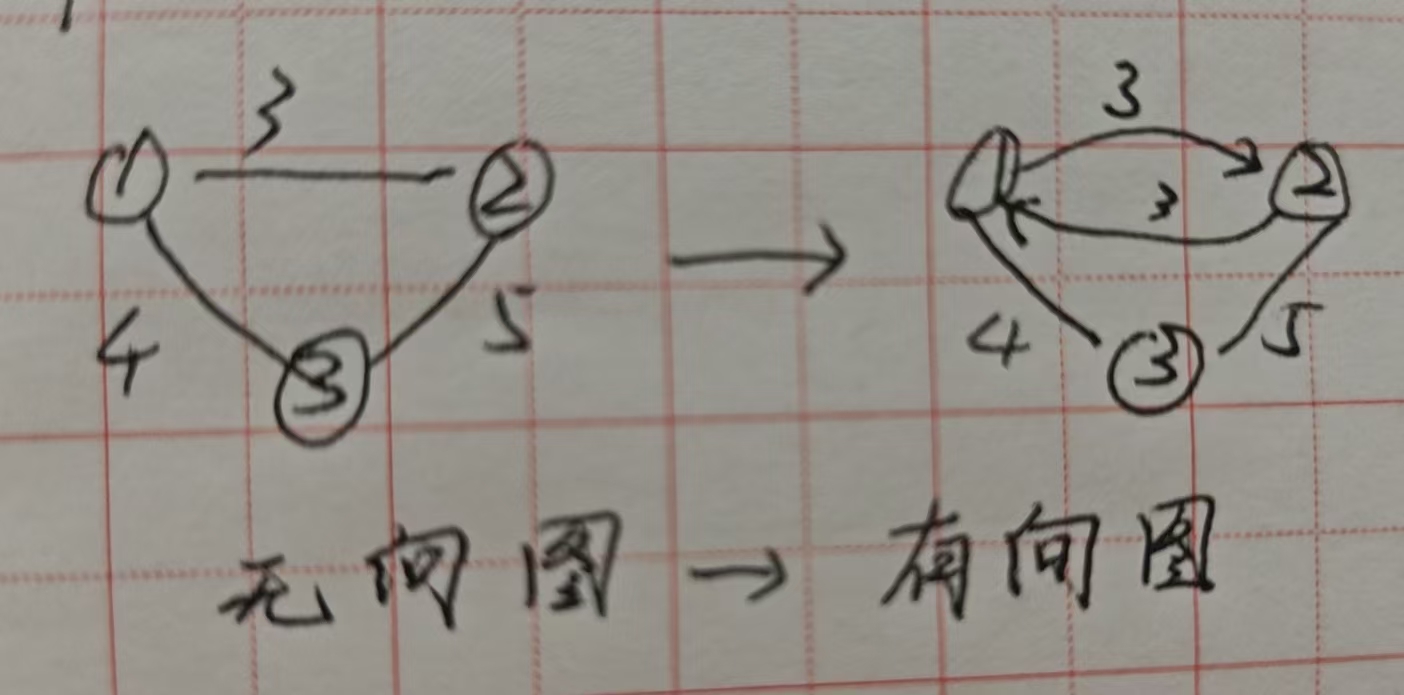
寻找逻辑如图:源点到其他顶点有直接路径的先找出,找出后再选择一个最小的作为源点,如此往复。
时间复杂度O(n2),要找到单个源点到其他顶点的最短路径此为n,最多要切换n个源点。
例子:
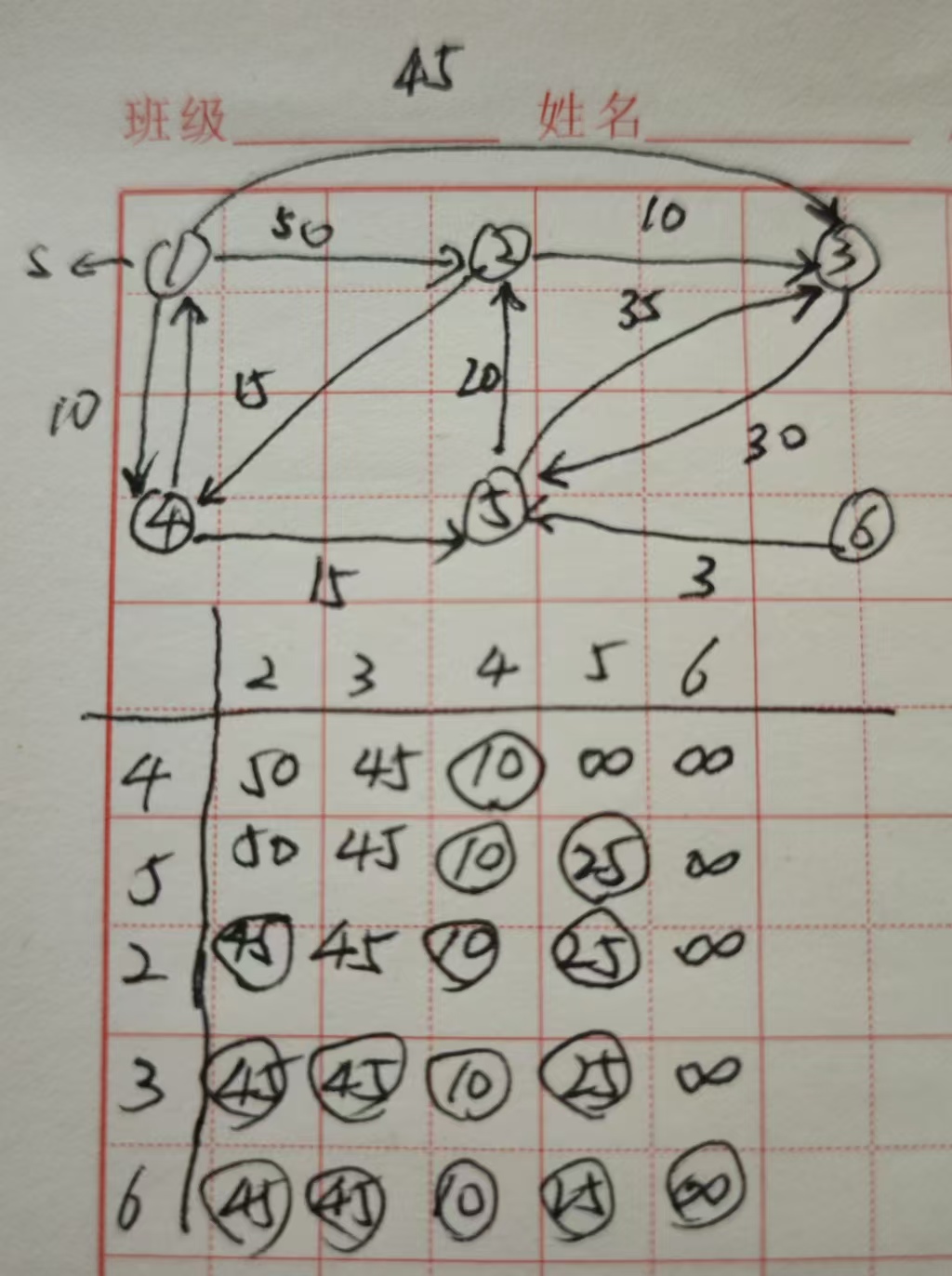
存在的问题:有负数的边可能会造成无效
