论文分享➲ ICLR2025 Oral | Scaling and evaluating sparse autoencoders

SCALING AND EVALUATING SPARSE AUTOENCODERS

稀疏自动编码器的规模扩展与评估

📖导读：本篇博客有🦥精读版、🐇速读版及🤔思考三部分；精读版是全文的翻译，篇幅较长；如果你想快速了解论文方法，可以直接阅读速读版部分，它是对文章的通俗解读；思考部分是个人关于论文的一些拙见，欢迎留言指正、探讨。最佳排版建议使用电脑端阅读。

---

目录

---

🦥精读版

Abstrct

  稀疏自动编码器是一种颇具前景的无监督方法，它通过从稀疏瓶颈层重构激活值，实现从语言模型中提取可解释的特征。由于语言模型学习了众多概念，自动编码器需要达到非常大的规模，才能够恢复所有相关特征。然而，研究自动编码器的规模扩展特性颇具难度，这是因为需要在重构目标和稀疏性目标之间取得平衡，并且还存在 “死亡隐层单元” 的情况。我们提出使用 k - 稀疏自动编码器（Makhzani & Frey, 2013）来直接控制稀疏性，这简化了调优过程，并提升了重构与稀疏性之间的平衡水平。此外，我们还发现了一些改进方法，即使在我们所尝试的最大规模下，这些方法也只会产生极少的 “死亡隐层单元”。利用这些技术，我们找到了关于自动编码器规模和稀疏性的清晰的规模扩展规律。我们还引入了几种新的指标，用于基于对假设特征的恢复情况、激活模式的可解释性以及下游影响的稀疏性来评估特征质量。这些指标通常都会随着自动编码器规模的增大而得到改善。为了展示我们方法的可扩展性，我们在 GPT-4 的激活值上对一个拥有 1600 万隐层单元的自动编码器进行了针对 400 亿个词元的训练。我们发布了适用于开源模型的代码和自动编码器，以及一个可视化工具。

1. Introduction

  稀疏自动编码器（SAEs）在寻找语言模型中的特征（Cunningham 等人，2023；Bricken 等人，2023；Templeton 等人，2024；Goh，2016）和电路（Marks 等人，2024）方面展现出了巨大的潜力。遗憾的是，由于其极高的稀疏性，稀疏自动编码器很难训练，因此以往的工作主要聚焦于在小型语言模型上训练相对较小的稀疏自动编码器。

  我们开发了一种先进的方法，可在任何语言模型的激活值上可靠地训练极宽且稀疏、几乎没有死亡隐层单元的自动编码器。我们系统地研究了与稀疏性、自动编码器大小和语言模型大小相关的缩放定律。为了证明我们的方法具有可靠的可扩展性，我们在 GPT - 4（OpenAI，2023）的残差流激活值上训练了一个拥有 1600 万个隐层单元的自动编码器。

  由于提高重构效果和稀疏性并非稀疏自动编码器的最终目标，我们还探索了更好的方法来量化自动编码器的质量。我们研究了以下几个方面的相关指标：某些假设特征是否被恢复、下游影响是否稀疏，以及特征能否以高精确率和高召回率进行解释。

  我们的贡献如下：
  1. 在第 2 节中，我们介绍了一种训练稀疏自动编码器的先进方案。
  2. 在第 3 节中，我们展示了清晰的缩放定律，并将其扩展到大量隐层单元的情况。
  3. 在第 4 节中，我们引入了隐层质量的评估指标，并发现根据这些指标，更大的稀疏自动编码器通常表现更好。

  我们还发布了代码、一套完整的 GPT - 2 小型自动编码器，以及一个用于 GPT - 2 小型自动编码器和 1600 万个隐层单元的 GPT - 4 自动编码器的特征可视化工具。

图1：基于GPT-4激活值训练的TopK自动编码器的缩放定律。（左图）在固定计算资源预算下的最优损失。（右图）在固定的隐层单元总数n和固定的稀疏度（激活的隐层单元数量）k条件下，收敛时损失的联合缩放定律。具体细节见第3部分。

2. 方法

2.1 实验设置

  输入：我们在GPT-2小型模型（Radford等人，2019）的残差流上，以及一系列规模逐渐增大且采用GPT-4架构和训练设置的模型（包括GPT-4本身（OpenAI，2023））的残差流上训练自动编码器。我们选择网络接近末端的一层，这一层应包含众多特征，且不专门用于预测下一个词元（更多讨论见F.1小节）。具体来说，对于GPT-4系列模型，我们使用网络中约 $\frac{5}{6}$ 位置处的一层；对于GPT-2小型模型，我们使用第8层（约 $\frac{3}{4}$ 的位置）。在所有实验中，我们采用的上下文长度为64个词元。在将输入传递给自动编码器（或计算重构误差）之前，我们会减去在维度 $d_{\text{model}}$ 上的均值，并将所有输入归一化为单位范数。

  评估：训练完成后，我们根据稀疏性 ${\text{L}}_0$ 和重构均方误差（MSE）来评估自动编码器。我们报告所有均方误差数值的归一化版本，方法是将其除以始终预测平均激活值时的基线重构误差。

  超参数：为简化分析，除非另有说明，我们不考虑学习率预热或衰减。我们在小规模实验中遍历不同的学习率，并推断出大规模实验中最优学习率的趋势。其他优化细节见附录A。

2.2 基线：ReLU自动编码器

  对于来自残差流的输入向量 $x\in {\mathbb{R}}^d$ 以及 $n$ 个隐层维度，我们采用（Bricken 等人，2023）提出的基线 ReLU 自动编码器。编码器和解码器的定义如下：$$\begin{gathered} z=\text{ReLU}(W_{\text{enc}}(x-b_{\text{pre}})+b_{\text{enc}}) \\ \hat{x}=W_{\text{dec}}z+b_{\text{pre}}\text{\hspace{1em}(1)} \end{gathered}$$其中 $W_{\text{enc}}\in {\mathbb{R}}^{n\times d}$，$b_{\text{enc}}\in {\mathbb{R}}^n$，$W_{\text{dec}}\in {\mathbb{R}}^{d\times n}$，且 $b_{\text{pre}}\in {\mathbb{R}}^d$。训练损失定义为 $\mathcal{L}=\Vert x-\hat{x}{\Vert }_2^2+\lambda \Vert z{\Vert }_1$，其中 $\Vert x-\hat{x}{\Vert }_2^2$ 是重构均方误差，$\Vert z{\Vert }_1$ 是用于促进隐层激活 $z$ 稀疏性的 ${\text{L}}_1$ 惩罚项，$\lambda$ 是一个需要调整的超参数。

图2：TopK激活函数与其他激活函数的比较。

2.3 TopK激活函数

  我们采用了$k$ - 稀疏自动编码器（Makhzani & Frey，2013），它通过使用一种激活函数（$\text{TopK}$）来直接控制激活的隐层单元数量。该激活函数仅保留k个最大的隐层单元值，其余的置为零。因此，编码器定义如下：
$$z=\text{TopK}(W_{\text{enc}}(x-b_{\text{pre}}))\text{\hspace{1em}(2)}$$ 解码器保持不变。训练损失简单定义为 $\mathcal{L}=\Vert x-\hat{x}{\Vert }_2^2$。

  使用k - 稀疏自动编码器有诸多好处：

• 它消除了对 ${\text{L}}_1$惩罚项的需求。 ${\text{L}}_1$是对 ${\text{L}}_0$的一种不完美近似，并且它会引入一种偏差，使得所有正的激活值都朝着零值缩小（见5.1小节）。
• 它能够直接设置 ${\text{L}}_0$，而无需调整 ${\text{L}}_1$系数$\lambda$，这使得模型比较更加简便，迭代速度更快。它还可以与任意激活函数结合使用。
• 从经验上看，在稀疏性与重构效果的平衡方面，它优于基线ReLU自动编码器（见图2a），并且随着规模的增大，这种差距还会进一步扩大（见图2b）。
• 通过有效地将较小的激活值限制为零，它提高了随机激活示例的单义性（见4.3小节） 。

2.4 防止出现“死亡隐层单元”

  “死亡隐层单元”是自动编码器训练过程中的另一个重大难题。在规模较大的自动编码器中，随着训练的进行，有越来越大比例的隐层单元会在某个时刻完全停止激活。例如，Templeton等人（2024年）训练了一个拥有3400万个隐层单元的自动编码器，但其中只有1200万个隐层单元处于激活状态。而且在我们进行的消融实验中发现，如果不采取任何缓解措施，“死亡隐层单元”的比例最高可达90%（图13）。这会导致均方误差（MSE）大幅恶化，并且使得训练在计算资源上造成浪费。

  我们发现了两种防止出现“死亡隐层单元”的重要方法：一是将编码器初始化为解码器的转置矩阵 ；二是使用一种辅助损失函数，该函数利用$\text{top-}{k}_{\text{aux}}$的“死亡隐层单元”来对重构误差进行建模（更多细节见A.2小节）。通过使用这些技术，即使是在我们规模最大的（拥有1600万个隐层单元的）自动编码器中，“死亡隐层单元”的比例也仅为7%。

3. 缩放定律

3.1 隐层单元数量

  鉴于像GPT - 4这样的前沿模型具有广泛的能力，我们假设要忠实地表示模型状态需要大量的稀疏特征。我们考虑两种主要方法来选择自动编码器的规模和词元预算：

图3：学习率随隐层单元数量共同变化的情况。每个点上方显示的是训练至收敛所需的词元数量。

图4：GPT-4系列中规模更大的目标模型，要达到相同的均方误差（k = 32），需要更多的隐层单元。

3.1.1 训练至计算 - 均方误差前沿（$L(C)$）

  首先，借鉴Lindsey等人（2024）的方法，在给定可用计算资源的情况下，我们训练自动编码器以达到最优的均方误差（MSE），而不考虑收敛情况。这种方法最初是用于预训练语言模型（Kaplan等人，2020；Hoffmann等人，2022）。我们发现，均方误差遵循计算量的幂律$L(C)$，不过最小的模型偏离了这一趋势（图1）。

  然而，隐层单元才是训练的重要产物（而非重构预测），而对于语言模型，我们通常只关心词元预测。因此，跨不同隐层单元数量n比较均方误差是不公平的——n越大，隐层单元的信息瓶颈越宽松，也就更容易实现更低的均方误差。所以，这种方法用于自动编码器训练可以说是缺乏理论依据的。

3.1.2 训练至收敛（$L(N)$）

  我们还研究了将自动编码器训练至收敛（在一定误差范围 $ϵ$ 内）的情况。如果不考虑计算效率，这为我们的训练方法所能达到的最佳重构效果设定了一个界限。在实践中，理想情况下我们会在 $L(N)$ 和 $L(C)$ 对应的词元预算之间选择一个中间值进行训练。

  我们发现，能使模型收敛的最大学习率与 $1/\sqrt{n}$ 成比例变化（图 3）。我们还发现，达到 $L(N)$ 时的最优学习率大约是达到 $L(C)$ 时最优学习率的四分之一。

  我们发现，对于 GPT - 2 小型模型，训练至收敛所需的词元数量大约以 $\Theta (n^{0.6})$ 的速率增长；对于 GPT - 4，该数量大约以 $\Theta (n^{0.65})$ 的速率增长（图 9）。这种增长趋势在某个点必然会失效——如果词元预算持续以低于线性的速率增长，那么每个隐层单元接收到梯度信号的词元数量将趋近于零。

3.1.3 不可约损失

  缩放定律有时会包含一个不可约损失项 $e$，使得公式为 $y=\alpha x^{\beta }+e$（Henighan 等人，2020）。我们发现，纳入一个不可约损失项能显著提高我们对 $L(C)$ 和 $L(N)$ 的拟合质量。

  起初，我们并不清楚为什么应该存在一个非零的不可约损失。一种可能性是，激活值中存在其他类型的结构。在极端情况下，激活值中的无结构噪声要进行建模会困难得多，并且其指数会接近零（附录 G）。存在一定的无结构噪声可以解释幂律曲线中的弯曲现象。

图5：在下游损失方面，TopK激活函数与其他激活函数的比较。本比较是基于GPT-2小型模型进行的，关于GPT-4的比较见 图11。

3.1.4 联合拟合稀疏性（$L(N,K)$）

  我们发现，均方误差（MSE）遵循关于隐层单元数量$n$和稀疏性水平$k$的联合缩放定律（图1b）。由于当$k$接近模型维度$d_{model}$时，重构变得毫无意义，所以这种缩放定律仅适用于$k$较小的情况。我们对GPT-4自动编码器进行联合缩放定律拟合得到的公式为：$$L(n,k)=\exp (\alpha +{\beta }_k\log (k)+{\beta }_n\log (n)+\gamma \log (k)\log (n))+\exp (\zeta +\eta \log (k))\text{\hspace{1em}(3)}$$ 其中$\alpha =-0.50$，${\beta }_k=0.26$，${\beta }_n=-0.017$，$\gamma =-0.042$，$\zeta =-1.32$，以及$\eta =-0.085$。我们可以看到$\gamma$是负数，这意味着随着$k$的增加，缩放定律$L(N)$的变化趋势会变得更陡峭。$\eta$也是负数，这表明不可约损失会随着$k$的增加而减小。

3.2 目标模型规模 $L_s(N)$

  由于语言模型的规模很可能会持续增大，我们也希望了解稀疏自动编码器如何随着目标模型的变化而进行缩放。我们发现，如果保持k不变，更大的目标模型需要更大规模的自动编码器才能达到相同的均方误差，并且其指数更差（图4）。

4. 评估

  我们在第3部分中展示了，更大规模的自动编码器在均方误差（MSE）和稀疏性方面表现出良好的缩放特性（另见5.2小节中关于激活函数的比较）。然而，自动编码器的最终目标并非仅仅是优化稀疏性与重构效果之间的平衡（在极限情况下这种平衡会退化），而是要找到对实际应用有用的特征，比如在机理可解释性方面。因此，我们使用以下指标来衡量自动编码器的质量：

1. 下游损失：如果将残差流隐层单元替换为自动编码器对该隐层单元的重构结果，那么此时语言模型的损失情况如何？（4.1小节）
2. 探测损失：自动编码器是否恢复了我们认为它们可能捕捉到的特征？（4.2小节）
3. 可解释性：对于自动编码器隐层单元的激活，是否存在既必要又充分的简单解释？（4.3小节）
4. 消融稀疏性：对单个隐层单元进行消融操作，是否会对下游的logits产生稀疏性影响？（4.5小节）

  这些指标表明，一般来说，随着隐层单元总数的增加，自动编码器的性能会变得更好。而激活的隐层单元数量${\text{L}}_0$所产生的影响则更为复杂。增加${\text{L}}_0$会使基于词元模式的解释效果变差，但会使探测损失和消融稀疏性得到改善。当${\text{L}}_0$接近模型维度$d_{\text{model}}$时，所有这些趋势也会失效，在这种情况下，隐层单元也会变得相当密集（详细讨论见E.5小节）。

图6：对于GPT-2小型自动编码器，探测损失和对数几率差值指标作为隐层单元总数n和激活隐层单元数量k的函数。一般来说，隐层单元总数越多（n值越高），所有指标的表现越好（黄色表示更好的情况）。当激活隐层单元数量L0 = 512时，这两个指标的表现都变差，在这种情况下，解决方案是密集的（见E.5小节）。

4.1 下游损失

  重构误差不为零的自动编码器，可能无法成功地对与（模型）行为最为相关的特征进行建模（Braun等人，2024）。为了衡量我们是否对与语言建模相关的特征进行了建模，我们参照先前的研究（Bills等人，2023；Cunningham等人，2023；Bricken等人，2023；Braun等人，2024），考虑使用下游的Kullback-Leibler（KL）散度和交叉熵损失。在这两种情况下，我们通过在正向传播过程中用重构值替换残差流，来测试自动编码器，并观察其对下游预测的影响。我们发现，与先前的方法相比，$k$-稀疏自动编码器在降低下游损失方面的效果，要比降低均方误差（MSE）的效果更显著（图5a）。我们还发现，当保持稀疏性${\text{L}}_0$固定，仅改变自动编码器的大小时，均方误差与KL散度以及交叉熵损失的差值之间，存在明确的幂律关系（图5b）。

  另一个问题是，仅靠原始损失数值本身很难进行解读——我们希望从绝对意义上了解其性能究竟有多好。先前的研究（Bricken等人，2023；Rajamanoharan等人，2024）将激活值归零的消融损失作为基线，并报告相对于该基线恢复的损失比例。然而，由于将残差流归零会导致极高的下游损失，这就意味着，即使对模型行为的解释非常糟糕，也可能获得较高的分数。

  相反，我们认为一个更合理的指标是，考虑训练一个具有可比下游损失的语言模型所需的预训练计算量的相对大小。例如，当我们将拥有1600万个隐层单元的自动编码器应用于GPT-4时，所得到的语言建模损失，相当于GPT-4预训练计算量的10%。

4.2 用一维探测法恢复已知特征

  如果我们期望一个高质量的自动编码器能够发现特定的特征（例如情感、语言识别等），那么衡量自动编码器质量的一个指标就是检查这些特征是否存在。基于这一思路，我们精心整理了一组包含61个二分类数据集（详细信息见表1）。对于每个任务，我们使用Newton-Raphson方法在每个latent上训练一个一维逻辑回归探测器来预测该任务，并记录（所有latents）最佳的交叉熵损失。即：$$\underset{i,w,b}{\min }\mathbb{E}\left[-y\log \sigma (w{z}_i+b)-(1-y)\log (1-\sigma (w{z}_i+b))\right]$$其中 $z_i$ 是第 $i$ 个激活前的隐层单元，$y$ 是一个二分类标签。我们对所有任务的损失求平均值。

  在 GPT-2 小型模型上的实验结果如图 6a 所示。我们发现，随着 $k$ 的增加，探测分数先上升后下降。我们发现，TopK 激活函数通常比 ReLU 激活函数能获得更好的探测分数（图 23），并且两者都比直接使用残差流通道的效果要好得多。关于几个 GPT-4 自动编码器的实验结果见图 32：我们观察到，尽管没有监督训练信号，但这一指标在整个训练过程中都有所改善；并且我们发现，它优于使用残差流通道的基线方法。按组件细分的分数结果见图 33。

  这一指标的优点是计算成本较低。然而，它也有一个主要的局限性，即它严重依赖于对哪些特征是 “自然” 特征的强假设。

4.3 为特征寻找简单的解释

  从经验来看，我们的自动编码器发现了许多特征，当查看随机激活值时，这些特征呈现出易于识别的模式，这些模式可用于给出解释（E.1小节）。然而，这可能会产生一种可解释性的“错觉”（Bolukbasi等人，2021），即解释过于宽泛，因此具有较高的召回率但精确率较低。例如，Bills等人（2023）提出了一种自动可解释性评分，该评分在很大程度上依赖于召回率。他们发现一个特征在短语“don’t stop”或“can’t stop”结尾处激活，但对所有包含“stop”的情况都激活的一种解释却能获得较高的可解释性分数。随着我们扩大自动编码器的规模，特征变得更加稀疏和具体，这种问题会变得更加严重。

  遗憾的是，正如Bills等人（2023）的研究那样，当使用GPT-4进行模拟时，评估精确率的成本极高。作为初步探索，我们专注于改进版的“神经元到图”（N2G）方法（Foote等人，2023），这是一种表达能力相对较弱但成本低得多的方法，它以带通配符的n元组集合的形式输出解释。未来，我们希望探索一些方法，以便更易于对任意英文解释的精确率进行近似评估。

  为构建一个N2G解释，我们从一些能激活隐层单元的序列开始。对于每个序列，我们找到仍能激活该隐层单元的最短后缀。然后，我们检查n元组中的任何位置是否可以用填充标记替换，以插入通配符标记。我们还通过检查在开头插入填充标记是否有影响，来判断该解释是否依赖于绝对位置。我们使用最多16个非零激活的随机样本来构建图，并使用另外16个作为真正例来计算召回率。

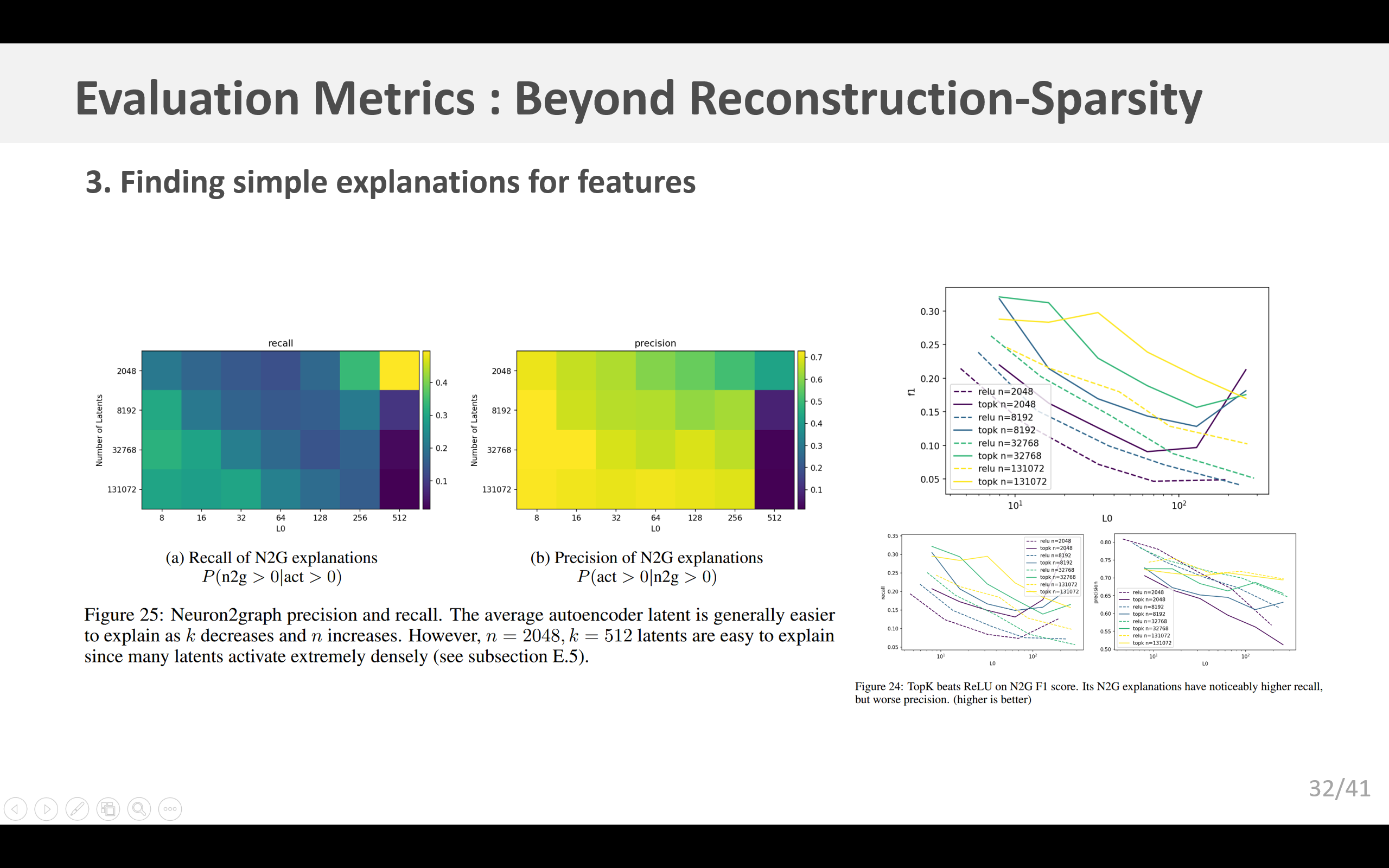
  GPT-2小型模型的结果见图25a和25b。请注意，密集的词元模式很容易解释，因此n = 2048，k = 512的隐层单元平均来说很容易解释，因为许多隐层单元的激活非常密集（见E.5小节）。一般来说，总隐层单元数量更多且激活隐层单元数量更少的自动编码器最容易用N2G进行建模。

  我们还得到证据表明，$\text{TopK}$模型的虚假正激活比ReLU模型更少。对于具有相同$n$（从而得到更好的F1分数）和相似${\text{L}}_0$的$\text{TopK}$模型，N2G解释的召回率显著更高（>1.5x），而精确率仅略微更低（>0.9x）（图24）。

4.4 解释重构

  当我们的目标是让模型的激活值具有可解释性时，我们可以提出这样一个问题：如果我们只使用模型中可解释的部分，那么会牺牲多少性能呢？

  我们的下游损失指标衡量的是我们捕获了多少性能（但我们的特征可能是不可解释的），而我们基于解释的指标衡量的是我们的特征具有多大程度的单义性（但它们可能无法解释模型的大部分内容）。这表明可以将我们的下游损失指标和基于解释的指标结合起来，方法是使用我们的解释来模拟自动编码器的隐层单元，然后在解码后检查下游损失。这个指标还有一个优点，即它以一种符合原则的方式同时重视召回率和精确率，并且对于激活更密集的隐层单元，它会更加重视召回率。

  我们用“神经元到图”（N2G）的解释方法尝试了这一点。N2G基于前缀树中的节点生成一个模拟值，但我们对这个值进行缩放，以最小化解释的方差。具体来说，我们计算$E[sa]/E[s^2]$，其中$s$是模拟值，$a$是真实值，并且我们在一个词元训练集上估计这个量。GPT-2模型的结果如图7所示。

图7：在GPT-2模型第8层，对残差流进行各种干预后的下游损失情况。当使用“神经元到图”（N2G）方法对自动编码器中的每个隐层单元进行解释，并且使用N2G模拟值而非真实的隐层单元激活值来运行模型时（紫色曲线），我们发现规模更大且更稀疏的自动编码器具有更低的下游损失。在最佳情况下，使用N2G模拟的隐层单元来运行模型，其性能优于二元语法语言建模的基线方法，这表明达到了一定程度的有效解释。然而，原始自动编码器的大部分重构结果（红色曲线）仍然无法用N2G的解释方法来解释。

4.5 消融影响的稀疏性

  如果语言模型所学习到的底层计算是稀疏的，那么一个假设是，自然特征不仅在激活值方面是稀疏的，而且在下游影响方面也是稀疏的（Olah等人，2024）。从经验上看，我们观察到消融影响通常是可解释的（见我们的可视化工具）。因此，我们开发了一个指标来衡量对输出对数几率（logits）的下游影响的稀疏性。

  在特定的词元索引处，我们获取残差流中的隐层单元，然后逐个消融自动编码器的每个隐层单元，并比较消融前后得到的对数几率。这个过程会为每次消融和受影响的词元产生$V$个对数几率差异，其中$V$是词元词汇表的大小。由于每个对数几率上的固定差异不会影响经过softmax后的概率，我们会在每个词元处减去对数几率差异值的中位数。最后，我们将在一组$T$个未来词元（在被消融的索引处或之后）上的这些向量连接起来，以得到一个总共$V\cdot T$个数值的向量。然后，我们通过$(\frac{{\text{L}}_1}{{\text{L}}_2}{)}^2$来衡量这个向量的稀疏性，这对应于“受影响的有效词元数量”。我们将其除以$V\cdot T$，以得到一个介于$0$到$1$之间的分数，分数越小表示影响越稀疏。

  我们对在GPT-2小型模型第8层的多层感知器（MLP）后残差流上训练的各种自动编码器进行了此操作，其中$T=16$。结果如图6b所示。令人欣喜的是，使用较大$k$值训练的模型，其隐层单元的影响更稀疏。然而，在$k=512$时趋势发生了逆转，这表明当$k$接近$d_{model}=768$时，自动编码器学习到的隐层单元的影响变得不太容易解释。请注意，隐层单元在绝对意义上是稀疏的，其$(\frac{L1}{L2}{)}^2$为$10$-$14\%$，而消融残差流通道得到的值为$60\%$（略好于随机向量的理论值$\sim \frac{2}{\pi }$）。

图8：可以对隐层单元激活值进行优化，以改善从一组固定隐层单元得到的重构效果。对于ReLU自动编码器，这种优化倾向于正值，这与补偿由L1惩罚项导致的激活值收缩情况相符。对于TopK自动编码器，优化过程没有偏向性，并且优化幅度也较小。这种优化仅缩小了ReLU自动编码器和TopK自动编码器之间的部分差距。

5. 理解TopK激活函数

5.1 TopK防止激活值收缩

  L1惩罚项的一个主要缺点是它倾向于将所有激活值向零收缩（Tibshirani，1996）。我们提出的TopK激活函数可以防止激活值收缩，因为它完全消除了对L1惩罚项的需求。为了从经验上衡量激活值收缩的程度，我们考虑在给定固定解码器的情况下，不同（且可能更大）的激活值是否会带来更好的重构效果。我们首先运行编码器以获得一组激活的隐层单元，保存稀疏掩码，然后仅优化非零值以最小化均方误差（MSE）。这种优化方法已经被多次提出，例如在k奇异值分解（k-SVD）（Aharon等人，2006）、松弛套索回归（relaxed Lasso）（Meinshausen，2007）或迭代阈值算法（ITI）（Maleki，2009）中。我们使用投影梯度下降法，在存在正值约束的情况下求解最优激活值。

  这种优化过程平均而言往往会增加ReLU模型中的激活值，但在TopK模型中却不会（图8a），这表明TopK不受激活值收缩的影响。TopK模型中优化的幅度也比ReLU模型小。在ReLU模型和TopK模型中，优化过程都显著改善了重构均方误差（图8b），以及下游的下一词元预测交叉熵（图8c）。然而，这种优化仅缩小了ReLU模型和TopK模型之间的部分差距。

5.2 与其他激活函数的比较

  近期关于稀疏自动编码器的其他研究提出了不同的方法来解决L1激活值收缩问题，并在帕累托意义上改进${\text{L}}_0$-$\text{MSE}$边界（Wright & Sharkey，2024；Taggart，2024；Rajamanoharan等人，2024）。Wright和Sharkey（2024）建议针对每个隐层单元微调一个缩放参数，以纠正${\text{L}}_1$激活值收缩问题。在门控稀疏自动编码器（Rajamanoharan等人，2024）中，哪些隐层单元激活的选择与激活幅度的估计是分开的。这种分离使得自动编码器能够更好地估计激活幅度，并避免${\text{L}}_1$激活值收缩。另一种方法是用概率ReLU（ProLU）（Taggart，2024）（也称为TRec（Konda等人，2014），或跳跃ReLU（JumpReLU）（Erichson等人，2019））来代替ReLU激活函数，它将所有低于正阈值的值设为零，即$J_{\theta }(x)=x\cdot 1_{(x>\theta )}$。由于参数$\theta$是不可微的，因此它需要一个近似梯度，比如ReLU等价梯度（ProLU-ReLU）或直通估计器（ProLU-STE）（Taggart，2024）。

  我们从重构均方误差、激活的隐层单元数量L0以及下游交叉熵损失等方面对这些不同的方法进行了比较（图2和图5）。我们发现，它们显著改善了重构-稀疏性的帕累托边界，其中TopK方法总体表现最佳。

6. 局限性与未来方向

  我们认为，我们的自动编码器仍有许多可以改进的地方。

• TopK激活函数强制每个词元恰好使用$k$个隐层单元，这可能并非最优选择。理想情况下，我们应该约束激活隐层单元数量的期望值$\mathbb{E}[L_0]$，而非$L_0$本身。
• 优化过程很可能可以大幅改进，例如采用学习率调度策略 、使用更好的优化器，以及设计更有效的辅助损失函数来防止出现“死亡隐层单元”。
• 在理解哪些指标最能有效追踪与下游应用的相关性，以及深入研究这些应用本身方面，还有很多工作可以开展。这些应用包括：寻找用于引导模型行为的向量、进行异常检测、识别模型中的电路结构等等。
• 我们对将混合专家（MoE）（Shazeer等人，2017）与自动编码器相结合的研究方向感到兴奋，这将大幅降低自动编码器训练的渐进成本，并支持训练规模更大的自动编码器。
• 我们发现的许多特征的随机激活，尤其是在GPT-4中，尚未达到足够的单语义性。我们相信，随着技术的改进和规模的扩大，这一问题有可能得到解决。
• 我们基于探测的评估指标存在较大的噪声，这可以通过纳入更广泛的任务以及提高任务质量来加以改善。
• 虽然我们使用“神经元到图”（n2g）方法是因其计算效率较高，但它只能捕捉非常简单的模式。我们认为，在开发更具表现力且计算成本足够低，能够通过模拟来估计解释精确率的解释方法方面，仍有很大的改进空间。
• 64个词元的上下文长度可能太短，无法展现出GPT-4最有趣的行为。

7. 相关研究

  Mallat和Zhang（1993）引入了在超完备字典上进行稀疏编码的概念。Olshausen和Field（1996）对这一想法进行了改进，提出在无监督的情况下从数据中学习字典。这种方法在图像处理领域尤其具有影响力，例如在（Mairal等人，2014）的研究中就有所体现。后来，Hinton和Salakhutdinov（2006）提出了自动编码器架构用于降维。结合这些概念，稀疏自动编码器得以发展（Lee等人，2007；Le等人，2013；Konda等人，2014），通过使用如L1惩罚项这样的稀疏先验来训练自动编码器，以提取稀疏特征。Makhzani和Frey（2013）通过引入k - 稀疏自动编码器进一步完善了这一概念，该自动编码器使用TopK激活函数替代了L1惩罚项。Makelov等人（2024）使用一种衡量从先前发现的电路中恢复特征能力的指标来评估自动编码器。

  最近，稀疏自动编码器被应用于语言模型（Yun等人，2021；Lee Sharkey，2022；Bricken等人，2023；Cunningham等人，2023），并且多个稀疏自动编码器已在小型开源语言模型上进行了训练（Marks，2023；Bloom，2024；Mossing等人，2024）。Marks等人（2024）表明，稀疏自动编码器得到的特征可以在语言模型中找到稀疏电路。Wright和Sharkey（2024）指出，稀疏自动编码器会受到L1惩罚项导致的激活值收缩问题的影响，L1惩罚项的这一特性最早由Tibshirani（1996）描述。Taggart（2024）和Rajamanoharan等人（2024）提出使用不同的激活函数来解决稀疏自动编码器中的激活值收缩问题。Braun等人（2024）建议在下游的KL散度上训练稀疏自动编码器，而非在重构均方误差上进行训练。

  Kaplan等人（2020）研究了语言模型的缩放定律，考察了损失如何随着各种超参数的变化而变化。Clark等人（2022）使用双线性拟合探索了与稀疏性相关的缩放定律。Lindsey等人（2024）专门研究了自动编码器的缩放定律，将损失定义为重构和稀疏性之间的特定平衡（而不是简单地在保持稀疏性固定的情况下关注重构）。

图9：词元预算、均方误差（MSE）以及学习率的幂律关系，这些数据是在不同k值上取平均值得到的结果。第一行展示的是GPT-2的情况，第二行展示的是GPT-4的情况。请注意，由于对学习率的扫描（取值测试）比较粗略，并且词元预算取决于学习率，所以各个拟合结果存在一定的噪声（尤其是对于GPT-4而言）。

A. 优化

A.1 初始化

  我们按如下方式初始化自动编码器：

• 依据Bricken等人（2023）的方法，将偏置 $b_{pre}$ 初始化为一组数据点样本集的几何中位数。
• 将编码器方向初始化为与相应的解码器方向平行，这样对应的隐层单元读写方向就相同。方向是均匀随机选取的。
• 按照Bricken等人（2023）的做法，在初始化时（以及在每个训练步骤之后），我们将解码器隐层单元方向缩放为单位范数。
• 对于基线模型，我们使用PyTorch的默认方式来初始化编码器的幅度。对于TopK模型，我们初始化编码器的幅度，使得重构向量的幅度与输入向量的幅度相匹配。不过，在我们的消融实验中发现，这要么没有影响，要么有微弱的负面作用（图14）。

A.2 辅助损失

  我们定义了一种类似于“幽灵梯度”（Jermyn & Templeton，2024）的辅助损失（AuxK），它使用top-$k_{aux}$个“死亡隐层单元”（通常$k_{aux}=512$）来对重构误差进行建模。在训练过程中，如果某些隐层单元在预先设定数量的词元（通常为1000万个）内都未激活，那么这些隐层单元就会被标记为“死亡”。然后，给定主模型的重构误差$e=x-\hat{x}$，我们定义辅助损失$L_{aux}=||e-\hat{e}|{|}_2^2$，其中$\hat{e}=W_{dec}z$是使用top-$k_{aux}$个“死亡隐层单元”进行的重构。完整的损失函数则定义为$L+\alpha L_{aux}$，其中$\alpha$是一个较小的系数（通常为$1/32$）。由于编码器的前向传播过程可以共享（并且其计算成本在解码器成本和编码器反向传播成本中占主导地位，详见附录D），添加这种辅助损失只会使计算成本增加约10%。

  我们发现，在大规模训练时，AuxK损失偶尔会出现非数字（NaN）的情况，当它为NaN时，我们会将其置零，以防止训练过程崩溃。

A.4 批量大小

  较大的批量大小对于实现更高程度的并行性至关重要。先前的研究往往使用如2048或4096个词元这样的批量大小（Bricken等人，2023；Conerly等人，2024；Rajamanoharan等人，2024）。为了获得并行处理的优势，在我们的大多数实验中，我们使用了131,072个词元的批量大小。

  虽然批量大小会显著影响$L(C)$损失，但我们发现，当优化超参数设置适当时，$L(N)$损失对批量大小的依赖并不强烈（图10）。

C. 训练消融实验

C.1 防止隐层单元“死亡”

图13：减少“死亡”隐层单元数量的方法（GPT-2小型模型，200万个隐层单元，k = 32）。采用辅助损失（AuxK）和/或关联初始化方案后，“死亡”隐层单元的数量在训练初期出现激增之后，通常会在训练过程中逐渐减少。

  我们发现，“死亡”隐层单元数量的减少主要得益于辅助损失（AuxK）和关联初始化方案的结合使用。

D. 系统相关

  如果没有我们在系统方面所做的改进，要在本文中把自动编码器扩展到最大规模是不可行的。一旦参数无法全部存储在一块GPU上，模型并行就变得很有必要。在最大规模的情况下，一个简单粗糙的实现方式可能会比我们经过优化的实现方式慢一个数量级。

D.1 并行处理

  我们采用标准的数据并行和张量分片方法（Shoeybi等人，2019），并且在TopK前向传播过程中额外使用了全收集（allgather）操作，以确定在全局范围内哪些$k$个隐层单元属于前$k$个（激活值较高的隐层单元）。为了将这种全收集操作的成本降至最低，我们将每个分片的容量因子截断为$2$ —— 进一步的改进是有可能的，但这需要对NCCL（英伟达集合通信库）进行修改。对于最大规模（1600万个隐层单元）的自动编码器，我们使用了$512$路分片。较大的批量大小（A.4小节）对于减少并行化开销非常重要。

  由于层数极少，这给并行处理带来了挑战 —— 它使得流水线并行（Huang等人，2019）和全分片数据并行（FSDP，Zhao等人，2023）方法不适用。此外，由于层数较少，通信重叠的机会也有限，尽管我们确实将主机到设备的传输操作和编码器数据并行通信操作进行了重叠，以实现一些微小的性能提升。

D.2 内核

  我们可以利用隐层单元的极高稀疏性，与单纯进行密集矩阵乘法相比，使用少得多的计算量和内存来执行大多数操作。在扩展到大量隐层单元时，这一点非常重要，既能直接提高处理吞吐量，又能减少内存使用量。

  我们使用两种主要的内核：

• DenseSparseMatmul：一种密集矩阵与稀疏矩阵之间的乘法运算。
• MatmulAtSparseIndices：在一组稀疏索引上对两个密集矩阵进行乘法运算。

  然后，我们进行了以下优化：

1. 解码器的前向传播使用 DenseSparseMatmul 内核。
2. 解码器的梯度计算使用 DenseSparseMatmul 内核。
3. 隐层单元的梯度计算使用 MatmulAtSparseIndices 内核。
4. 编码器的梯度计算使用 DenseSparseMatmul 内核。
5. 偏置前的梯度计算使用了一个技巧，即在与编码器权重相乘之前，先在批次维度上对激活前的梯度进行求和。

  从理论上讲，在极限稀疏的情况下，这能使计算效率提高多达6倍，因为编码器的前向传播是唯一剩下的密集型操作。在实践中，我们确实发现编码器的前向传播占据了大部分计算量，而激活前的值占据了大部分内存。

  为了确保读取操作能够合并进行，解码器权重矩阵的存储方式也必须与典型布局不同，要进行转置存储。我们还使用了许多其他内核来融合各种操作，以减少内存和内存带宽的使用。

F. 各类小结果

F.1 不同位置的影响

  在对GPT-2小型模型的不同位置进行全面测试时，我们发现，最优学习率会因层以及位置类型（多层感知器（MLP）增量、注意力增量、MLP后置、注意力后置）的不同而有所变化，但变化幅度在两倍以内。

  收敛所需的词元数量在前几层明显更高。均方误差（MSE）在残差流的前几层是最低的，随后逐渐增加，直到最后一层时有所下降。残差流增量的均方误差在第6层左右达到峰值，注意力增量的均方误差在最后一层急剧下降。

  当对重构结果进行消融操作时，下游损失和KL散度会随着层数的增加而明显变差。尽管归一化均方误差在较后的层中会下降。然而，在最后几层似乎存在一个例外（GPT-2小型模型的第11/12层，尤其是第12/12层），这些层的归一化均方误差可能会比前几层更好，但对下游预测的影响却更严重（图27）。

  我们还可以看到，层的选择对不同的指标有着不同的影响（图28）。不出所料，较前的层能得到更好的“神经元到图”（N2G）解释，而后层在探测损失和稀疏性方面表现更优。

  在使用在GPT-2小型模型最后一层上训练的自动编码器的早期实验结果中，我们发现，从性质上来说，其结果比在第8层上训练的结果要差，所以在后续的所有实验中我们都使用第8层。

G. 不可约损失项

  在语言模型中，不可约损失的存在是因为文本具有一些内在的不可预测性——即使是一个完美的语言模型，预测下一个词元的损失也不可能为零。由于理论上一个足够大的自动编码器实际上能够完美地重构输入，我们最初预计不会存在不可约损失项。然而，我们发现，如果没有不可约损失项，拟合的质量会大幅下降。

  虽然我们没有完全理解不可约损失项背后的原因，但我们的假设是，激活值是由一系列具有不同结构量的成分组成的。我们预计结构较少的数据也会有更差的缩放指数。在最极端的情况下，一部分激活值可能完全是无结构的高斯噪声。在对无结构噪声进行的模拟实验中（见图31），我们发现在768维高斯数据上的$L(N)$指数为$-0.04$，这比我们在类似维度的GPT-2小型模型激活值上看到的大约$-0.26$要平缓得多。

图31：在768维随机高斯数据上进行训练时的L(N)缩放定律，其中k = 32 。

---

🐇速读版

1. 论文解读

【注】这部分我将以幻灯片的形式展示论文的主要内容，如感兴趣可留言获取原始PPT文件，欢迎留言讨论哈！

  以上就是这篇文章的主要内容。此外，研究团队还提供了一个可视化交互界面SAE viewer，用于直观展示SAE提取到的特征，感兴趣的读者可以点击进入体验一下。

---

2. 代码

这篇论文公开了官方代码，为后续研究GPT系列模型内部特征可解释性提供了重要工具支持。但目前只提供了在GPT-2-small上训练的四个不同尺寸的SAE（如下代码所示）。大概计算了一下，GPT-2-small（12层）上训练的SAE（n=32768）参数量大约为0.6B。感兴趣的读者可以 clone 项目亲自运行，进一步探索其工作机制。欢迎留言讨论哈！

def v1(location, layer_index):"""Details:- Number of autoencoder latents: 32768- Number of training tokens: ~64M- Activation function: ReLU- L1 regularization strength: 0.01- Layer normed inputs: false- NeuronRecord files:`az://openaipublic/sparse-autoencoder/gpt2-small/{location}/collated_activations/{layer_index}/{latent_index}.json`"""assert location in ["mlp_post_act", "resid_delta_mlp"]assert layer_index in range(12)return f"az://openaipublic/sparse-autoencoder/gpt2-small/{location}/autoencoders/{layer_index}.pt"def v4(location, layer_index):"""Details:same as v1"""assert location in ["mlp_post_act", "resid_delta_mlp"]assert layer_index in range(12)return f"az://openaipublic/sparse-autoencoder/gpt2-small/{location}_v4/autoencoders/{layer_index}.pt"def v5_32k(location, layer_index):"""Details:- Number of autoencoder latents: 2**15 = 32768- Number of training tokens:  TODO- Activation function: TopK(32)- L1 regularization strength: n/a- Layer normed inputs: true"""assert location in ["resid_delta_attn", "resid_delta_mlp", "resid_post_attn", "resid_post_mlp"]assert layer_index in range(12)# note: it's actually 2**15 and 2**17 ~= 131kreturn f"az://openaipublic/sparse-autoencoder/gpt2-small/{location}_v5_32k/autoencoders/{layer_index}.pt"def v5_128k(location, layer_index):"""Details:- Number of autoencoder latents: 2**17 = 131072- Number of training tokens: TODO- Activation function: TopK(32)- L1 regularization strength: n/a- Layer normed inputs: true"""assert location in ["resid_delta_attn", "resid_delta_mlp", "resid_post_attn", "resid_post_mlp"]assert layer_index in range(12)# note: it's actually 2**15 and 2**17 ~= 131kreturn f"az://openaipublic/sparse-autoencoder/gpt2-small/{location}_v5_128k/autoencoders/{layer_index}.pt"# NOTE: we have larger autoencoders (up to 8M, with varying n and k) trained on layer 8 resid_post_mlp
# we may release them in the future

参考文献
@inproceedings{
gao2025scaling,
title={Scaling and evaluating sparse autoencoders},
author={Leo Gao and Tom Dupre la Tour and Henk Tillman and Gabriel Goh and Rajan Troll and Alec Radford and Ilya Sutskever and Jan Leike and Jeffrey Wu},
booktitle={The Thirteenth International Conference on Learning Representations},
year={2025},
url={https://openreview.net/forum?id=tcsZt9ZNKD}
}