软件工程之形式化说明技术深度解析

按照形式化的程度，可以把软件工程使用的方法划分成非形式化、半形式化和形式化3种。用自然语言描述需求规格说明书，是典型的非形式化方法。用数据流图或实体-联系图建立模型，是典型的半形式化方法。

所谓形式化方法，是描述系统性质的基于数学的技术，也就是说，如果一种有坚实数学基础，那么它就是形式化的。

前文基础：
1.软件工程学概述：软件工程学概述-CSDN博客 

2.软件过程深度解析：软件过程深度解析-CSDN博客 

3.软件工程之需求分析涉及的图与工具：软件工程之需求分析涉及的图与工具-CSDN博客 

一、概述

（一）非形式化方法的缺点

非形式化方法主要依赖自然语言描述系统需求和设计，其核心缺陷在于语义模糊性和逻辑不严谨性。具体表现为：

（1）矛盾性：同一需求可能存在相互冲突的陈述。例如，某系统需求文档中同时要求“用户必须通过短信验证”和“用户可选择跳过验证”，导致设计无法执行。

（2）二义性：同一描述可能被不同人解读为不同含义。例如，“系统应快速响应”中的“快速”缺乏量化标准，不同开发者可能设定不同阈值（如 1 秒、5 秒）。

（3）含糊性：表述笼统，缺乏具体细节。例如，“系统需具备良好的用户体验”未明确具体指标（如界面响应时间、操作步骤数）。

（4）不完整性：遗漏关键需求或约束条件。例如，某金融系统需求未明确“高并发下的交易一致性”，导致上线后出现数据不一致问题。

（5）抽象层次混乱：高层抽象与低层细节混杂。例如，在需求文档中同时描述业务流程和数据库表结构，导致逻辑层次不清。

（二）形式化方法的优点

形式化方法基于数学逻辑和符号系统，通过严格的数学模型描述系统行为，具有以下显著优势：

（1）精确性：使用数学语言消除歧义，确保需求定义唯一。例如，用一阶逻辑公式明确“所有用户必须登录”的语义。

（2）可验证性：通过数学证明或模型检查技术，验证系统是否满足预期性质。例如，使用模型检查工具SPIN验证通信协议的死锁自由性。

（3）早期错误检测：在开发早期发现设计缺陷，降低后期修改成本。例如，NASA在火星探测项目中使用形式化方法提前发现导航软件的逻辑错误。

（4）跨阶段平滑过渡：从需求规格到系统设计的数学模型可直接映射，支持无缝迭代。例如，Z语言的模式（Schema）可同时描述需求和设计，便于逐步细化。

（5）高可靠性保障：适用于安全关键系统（如航空航天、医疗设备）。例如，空客A320的飞行控制系统通过形式化验证，确保了99.999% 的可靠性。

（三）应用形式化方法的准则

（1）选择适当的表示方法：根据系统特性选择合适的形式化技术。例如，实时系统可采用时间自动机（Timed Automata），并发系统可采用Petri网。

（2）形式化但不过分形式化：仅对关键部分形式化，避免过度复杂。例如，对支付系统的交易逻辑进行形式化，而界面设计采用传统方法。

（3）估算成本与资源：需投入专业人力和工具，需提前评估培训和工具采购成本。例如，使用 Coq 进行定理证明需至少 6 个月的培训周期。

（4）结合传统方法：形式化方法与 UML、敏捷开发等结合，发挥互补优势。例如，用 Petri 网建模并发流程，同时用 UML 活动图描述业务逻辑。

（5）建立详尽文档：用自然语言注释形式化模型，提高可读性。例如，在 Z 语言规格说明中添加需求背景和验证结论。

（6）持续测试与验证：形式化验证无法覆盖所有场景，需结合黑盒测试和白盒测试。例如，对区块链智能合约进行形式化验证后，仍需通过压力测试验证性能。

二、有穷状态机

（一）概念

有穷状态机（Finite State Machine, FSM）是一种基于状态转移的形式化模型，由五元组定义：

（1）状态集Q：有限个状态的集合（如Q = { q0, q1, q2 }）。

（2）输入字母表Σ：输入符号的集合（如Σ= { a, b }）。

（3）状态转移函数δ：形式如δ: Q×Σ→ Q，定义状态间的转移规则。

（4）初始状态q0：系统的起始状态。

（5）终止状态集F ⊆Q：接受输入的状态集合。

FSM通过状态转移描述系统行为，适用于处理离散事件系统（如协议解析、流程控制）。

（二）例子：自动售货机控制系统

项目背景：某自动售货机支持投币、选择商品、退币等操作，需确保交易流程的正确性。

1.状态定义：

q0：初始状态（等待投币）。

q1：已投币状态（等待选择商品）。

q2：商品发放状态（处理出货）。

q3：退币状态（处理退币）。

2.转移函数：

投币（输入a）：δ(q0, a) = q1。

选择商品（输入b）：δ(q1, b) = q2。

退币（输入c）：δ(q1, c) = q3。

出货完成（输入d）：δ(q2, d) = q0。

退币完成（输入e）：δ(q3, e) = q0。

3.状态转移图：

q0 [投币a] → q1  

q1 [选商品b] → q2  

q1 [退币c] → q3  

q2 [出货d] → q0  

q3 [退币e] → q0  

4.流程说明：

（1）用户投币后进入q1，系统检查余额。

（2）若余额足够，选择商品进入q2，发放商品后返回q0。

（3）若余额不足或用户选择退币，进入q3，退币后返回q0。

数学模型：状态转移函数可表示为矩阵形式：

其中“-”表示无效转移。比如，不存在“q0 [投币a] → q2 [出货d]，因为需要先选择商品 ”。

三、Petri网

（一）概念

Petri网是一种图形化建模工具，用于描述并发和异步系统，由四元组C = (P, T, I, O)定义：

（1）库所（Place）P：用圆圈表示，代表系统状态或资源（如“可用打印机”）。

（2）变迁（Transition）T：用矩形表示，代表事件或操作（如“打印任务”）。

（3）输入函数I：定义库所到变迁的输入弧。

（4）输出函数O：定义变迁到库所的输出弧。

Petri网通过令牌（Token）在库所间的流动模拟系统动态行为，适用于分析并发、同步和死锁问题。

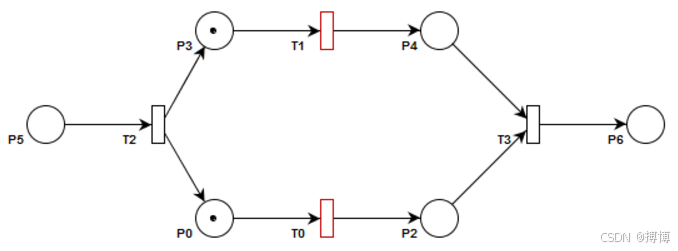
（二）例子：生产流水线控制系统

项目背景：某工厂流水线包含三个工序：加工（T1）、质检（T2）、包装（T3），需协调各工序的资源分配。

Petri 网模型：

1.库所：

P_1：原材料库存（初始有 3 个令牌）。令牌可以理解为资源的个数。

P_2：加工中（初始 0 个令牌）。

P_3：质检中（初始 0 个令牌）。

P_4：包装中（初始 0 个令牌）。

P_5：成品库（初始 0 个令牌）。

2.变迁：

T_1：加工（消耗 1 个P_1，生成 1 个P_2）。

T_2：质检（消耗 1 个P_2，生成 1 个P_3）。

T_3：包装（消耗 1 个P_3，生成 1 个P_4）。

T_4：完成（消耗 1 个P_4，生成 1 个P_5）。

关联矩阵：

其中“-1”表示消耗令牌，“+1”表示生成令牌。

3.动态行为分析：

初始状态：M_0 = (3, 0, 0, 0, 0)。

触发T_1：M_1 = (2, 1, 0, 0, 0)（加工中 1 个工件）。

触发T_2：M_2 = (2, 0, 1, 0, 0)（质检中 1 个工件）。

触发T_3：M_3 = (2, 0, 0, 1, 0)（包装中 1 个工件）。

触发T_4：M_4 = (2, 0, 0, 0, 1)（成品库 1 个工件）。

可达性分析： 通过状态方程（其中X为变迁触发向量），可验证系统能否达到目标状态。例如，目标状态M_target = (0, 0, 0, 0, 3)是否可达：

解得x_1 = x_2 = x_3 = x_4 = 3，因此可达。

四、Z语言

（一）简介

Z 语言是一种基于集合论和一阶谓词逻辑的形式化规格说明语言，通过模式（Schema）描述系统状态和行为。其核心要素包括：

1.类型定义：

使用集合、序列、映射等数学结构。

Person == ℕ  // 定义Person类型为自然数（身份证号）

2.模式：

封装状态变量和约束条件。

LoginSystem == [users: P Person;  // 用户集合loggedIn: Person → ℙ;  // 登录状态映射∀ p: Person • p ∈ loggedIn ⇒ p ∈ users  // 约束：登录用户必须在用户集合中]

3.操作定义：

通过模式描述状态转换。

LoginRequest == ΔLoginSystem  // Δ表示状态可修改∧ [p?: Person;  // 输入参数：用户IDp? ∈ users \ loggedIn;  // 前置条件：用户未登录loggedIn' = loggedIn ∪ { p? }  // 后置条件：登录状态更新]

应用案例： IBM在开发客户信息控制系统（CICS）时使用Z语言，将需求错误率降低了70%，开发成本减少9%。

（二）评价

1.优点：

（1）精确性：数学语义确保规格说明无歧义。例如，用集合论定义用户权限，避免自然语言描述的模糊性。

（2）可扩展性：模式可组合和重用。例如，将“用户登录”模式与“权限管理”模式组合，构建完整的访问控制系统。

（3）形式化验证支持：可通过定理证明工具（如 ProofPower）验证规格说明的一致性。例如，证明“登录操作不会导致重复登录”的性质。

2.缺点：

（1）学习曲线陡峭：需掌握集合论、逻辑推理和复杂符号。例如，理解Z语言的量化表达式需要数学基础。

（2）工具支持有限：主流IDE（如Eclipse）对Z语言的支持较弱，依赖专用工具（如Z/EVES）。

（3）不适用于实时系统：缺乏时间建模能力，难以描述时序约束（如“操作必须在5秒内完成”）。

3.工业应用现状：

Z语言在航空航天、金融等领域有成功案例，但受限于学习成本和工具生态，普及率低于UML等半形式化方法。例如，欧洲航天局在阿丽亚娜火箭项目中使用Z语言，但后续项目逐渐转向更易上手的模型驱动方法。

五、结语

形式化说明技术通过数学模型和逻辑推理提升软件系统的精确性和可靠性，尤其适用于安全关键领域。实际应用中需权衡成本与收益：

（1）有穷状态机适用于离散事件系统（如协议解析），通过状态转移图直观描述行为。

（2）Petri网擅长并发系统建模，通过关联矩阵和可达性分析揭示潜在问题。

（3）Z语言提供严格的数学规格说明，适合复杂系统的需求定义和验证。

未来，随着自动化验证工具（如Coq、SPIN）的发展和低代码技术的融合，形式化方法将逐步从实验室走向工业界，成为保障软件质量的核心技术之一。