当前位置：首页 > news >正文

SIFT算法详细原理与应用

news 来源：原创 2025/5/6 10:12:02

SIFT算法详细原理与应用

1 SIFT算法由来

1.1 什么是 SIFT？

SIFT，全称为 Scale-Invariant Feature Transform（尺度不变特征变换），是一种用于图像特征检测和描述的经典算法。它通过提取图像中的局部关键点，并为每个关键点生成具有尺度和旋转不变性的描述子，使其能够在不同的图像中进行特征匹配。SIFT 算法尤其适合处理视角变化、尺度变换、部分遮挡和光照变化的问题，因此被广泛应用于计算机视觉领域。

1.2 SIFT 的发展历程

SIFT 由计算机科学家 David G. Lowe 于 1999 年首次提出，并在 2004 年发表的论文《Distinctive Image Features from Scale-Invariant Keypoints》中进一步完善。其革命性的设计使得 SIFT 成为了特征提取领域的重要里程碑。
虽然 SIFT 曾因专利保护限制了开源使用，但随着专利过期（美国专利于 2020 年到期），SIFT 再次成为开源社区的重要工具，并在许多实际项目中被广泛应用。

此外，SIFT 的思想也启发了许多后续算法的诞生，例如 SURF（Speeded-Up Robust Features）和 ORB（Oriented FAST and Rotated BRIEF），进一步推动了特征提取技术的发展。

2 SIFT算法详细原理

根据高斯函数生成高斯金字塔
生成高斯金字塔的作用可以理解为通过相机调整距离物体的距离拍摄的物理，实际上对于物体本身，不管相机距离物体的距离远近，总有一些特征是不变的，比如物体的边缘及轮廓等。
高斯金字塔底层的图像可以理解为相机近距离拍摄物体的图像，顶层可以理解为相机远距离拍摄物体的图像。故sift具有图像尺寸不变性及旋转不变性（再生成种子时会进行角度旋转变换及归一化处理），而角点检测算法Harris只具有旋转不变性

通过模拟不同距离的图像，尽可能的找到图像的所有特征点
根据高斯金字塔生成差分金字塔（DOG）

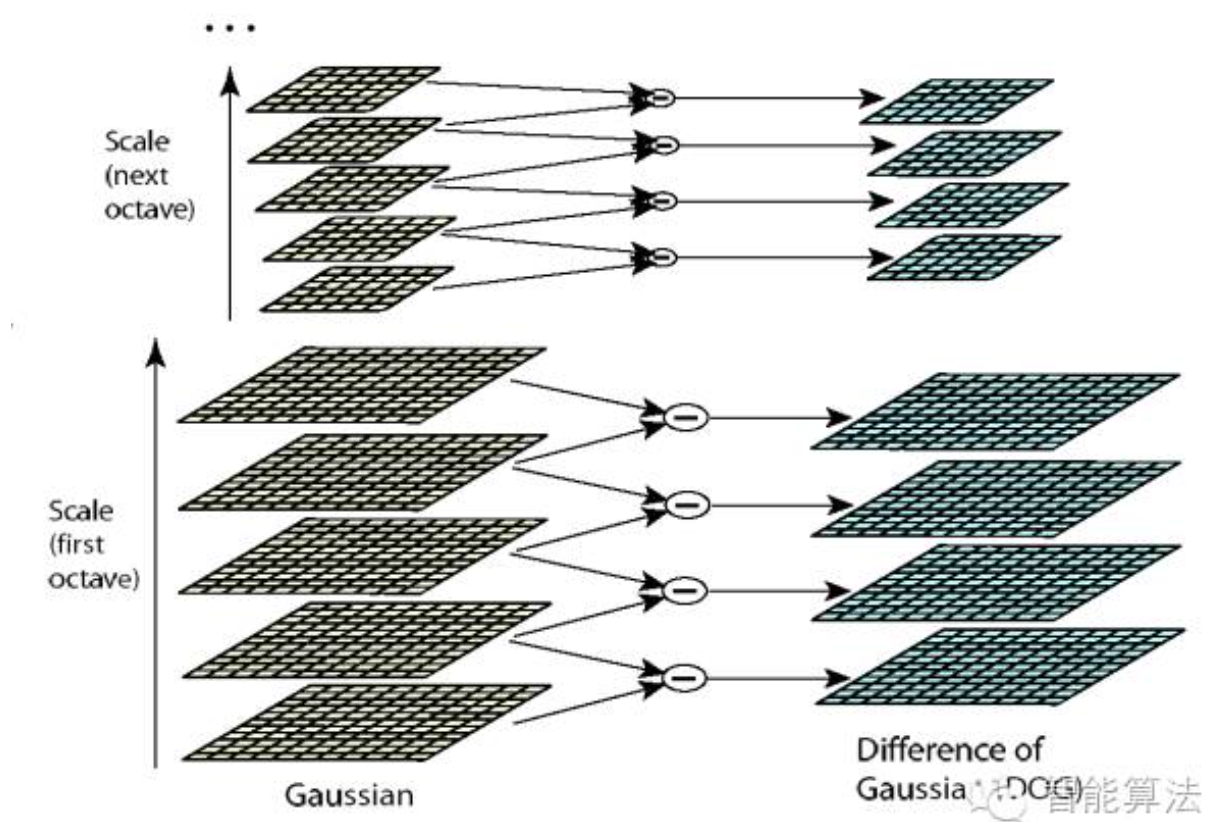
通过对高斯金字塔同一组中相邻的图像进行相减，得到DOG差分图像
根据DOG差分图像找到关键点（极值点）

为了寻找尺度空间的极值点，每一个采样点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。如图所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。一个点如果在DOG尺度空间本层以及上下两层的26个领域中是最大或最小值时，就认为该点是图像在该尺度下的一个特征点,如图所示。
关键点过滤
真正的关键点都是灰度值在，x,y方向都有变化的，即：一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向有较小的主曲率。
根据找到的关键点计算出对应的描述子
- 计算关键点周围领域的直方图(包括变化尺度，角度（角度可以分为8个方向）)，得出当前关键点的主方向（变换尺度最大的为主方向）
- 对关键点周围领域进行旋转，将主方向旋转成与x方向一致的方向，以确保旋转不变性
- 将关键点领域分为4x4的 16个子区域，每个子区域分别计算他们的直方图，然后生成由右图组成的16个种子，每个种子包含八个方向的变化尺度。
- 生成描述子
  根据关键点生成的16个种子的八维向量，组成一个4x4x8-128维的向量。再将特征向量进行归一化（就是使的特征向量的值1，成为单位向量）。即每一个关键点就能得到一个128维的向量，也成为一个关键点的描述子。
两个图像描述子的匹配
通过sift算法分别生成两个图像的各自的多个描述子，分别计算两个图像描述子向量之间的距离，计算两个向量的距离有多种
计算两个向量的距离有多种方式
- 曼哈顿距离欧氏距离
- 欧氏距离
- 切比雪夫距离
- 闵可夫斯基距离
- 标准化欧式距离
- 余弦距离
- 汉明距离
- 杰卡德距离
- 马氏距离
  具体详见：9个机器学习算法常见距离计算公式