C37.【C++ Cont】二叉树的存储方式和四种遍历
目录
1.定义
2.存储
顺序存储
链式存储
代码示例
3.遍历
知识回顾
静态实现方法下的遍历
1.前序遍历(又称先序遍历)
编辑
2.中序遍历
3.后序遍历
4.层序遍历(宽度优先遍历)
1.定义
参见100.【C语言】数据结构之二叉树的基本知识文章
2.存储
复习参见101.【C语言】数据结构之二叉树的堆实现(顺序结构) 1为动态存储,本文将使用之前文章讲过的静态方法来实现
顺序存储
设从根节点开始编号为1
1.存储完全二叉树:因为父子结点之间的编号可以用公式算出来,因此可根据编号依次将结点放在数组对应的位置上即可
2.存储非完全二叉树:补成完全二叉树再去编号,例如下图,空间利用率不高
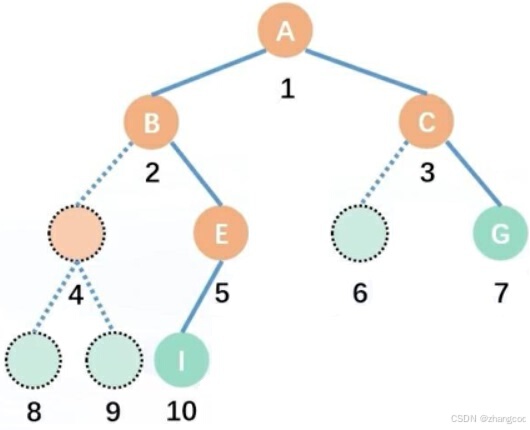

不建议对非完全二叉树或满二叉树使用顺序存储,可以用堆或者线段树
链式存储
定义:通过指针来表示二叉树中节点之间关系的存储方式
动态实现参见106.【C语言】数据结构之二叉树的三种递归遍历方式文章,本文讲静态实现
静态实现需要两个数组left[N]和right[N]用于存储每个节点的左右孩子节点
例如下图:
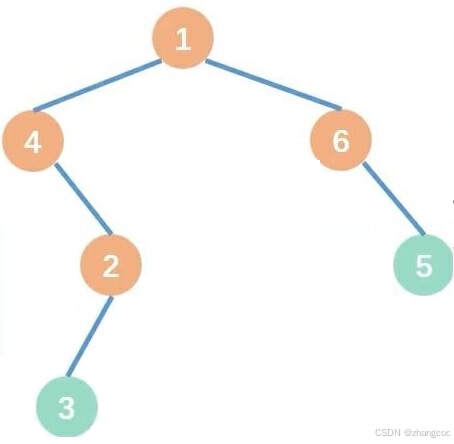
设数组下标为节点的编号,则存储结构left[N]和right[N]为:

(如果没有孩子节点,那么存0)
代码示例
有一个n(n<=10^6)个节点的二叉树.给出每个节点的两个子节点编号(均不超过n),建立一棵二叉树(根节点的编号为1),如果是叶子节点,则输入0 0
输入描述:第一行一个整数n,表示节点数;之后n行,第i行两个整数l和r,分别表示节点的左右子节点编号.若l=0则表示无左子节点,r=0同理.
#include <iostream>
using namespace std;
const int N=1e3+10;
int _left[N],_right[N],n;
int i=1;//根节点编号为1
int main()
{
cin>>n;
while(n--)
{
cin>>_left[i]>>_right[i];
i++;
}
return 0;
}这里_left和_right前都加了"_"避免冲突,因为Dev C++提示[Error] reference to 'left' is ambiguous和[Error] reference to 'right' is ambiguous
3.遍历
知识回顾
106.【C语言】数据结构之二叉树的三种递归遍历方式
静态实现方法下的遍历
由于竞赛中追求运行速度快,因此不用动态分配内存来实现,本文用静态实现方法来遍历,可利用DFS的思想实现三种遍历方式,以此图作为测试用例

窗口中输入
6
2 4
3 0
0 0
5 6
0 0
0 0
1.前序遍历(又称先序遍历)
代码
#include <iostream>
using namespace std;
const int N=1e3+10;
int _left[N],_right[N],n;
int i=1;
void preorder(int x)
{
cout<<x<<"-->";//先访问根
if (_left[x])//左子树不为空
preorder(_left[x]);
if (_right[x])//右子树不为空
preorder(_right[x]);
}
int main()
{
cin>>n;
while(n--)
{
cin>>_left[i]>>_right[i];
i++;
}
preorder(1);//设根节点编号为1
cout<<"结束";
return 0;
}执行结果
2.中序遍历
#include <iostream>
using namespace std;
const int N=1e3+10;
int _left[N],_right[N],n;
int i=1;
void inorder(int x)
{
if (_left[x])//左子树不为空
inorder(_left[x]);
cout<<x<<"-->";//访问根
if (_right[x])//右子树不为空
inorder(_right[x]);
}
int main()
{
cin>>n;
while(n--)
{
cin>>_left[i]>>_right[i];
i++;
}
inorder(1);//设根节点编号为1
cout<<"结束";
return 0;
}执行结果

3.后序遍历
代码
#include <iostream>
using namespace std;
const int N=1e3+10;
int _left[N],_right[N],n;
int i=1;
void postorder(int x)
{
if (_left[x])//左子树不为空
postorder(_left[x]);
if (_right[x])//右子树不为空
postorder(_right[x]);
cout<<x<<"-->";//访问根
}
int main()
{
cin>>n;
while(n--)
{
cin>>_left[i]>>_right[i];
i++;
}
postorder(1);//设根节点编号为1
cout<<"结束";
return 0;
}执行结果

4.层序遍历(宽度优先遍历)
和 文章一样,利用队列即可,但和无根树不同的是:二叉树不需要状态数组bool st[N]来标记节点是否访问过,因为二叉树是有序树
代码
#include <iostream>
#include <queue>
using namespace std;
const int N=1e3+10;
int _left[N],_right[N],n;
int i=1;
void bfs(int x)
{
queue<int> q;
q.push(x);
while(!q.empty())
{
int tmp=q.front();
q.pop();
cout<<tmp<<"-->";
if (_left[tmp])//左子树不为空
q.push(_left[tmp]);
if (_right[tmp])//右子树不为空
q.push(_right[tmp]);
}
}
int main()
{
cin>>n;
while(n--)
{
cin>>_left[i]>>_right[i];
i++;
}
bfs(1);
cout<<"结束";
return 0;
}执行结果


