【漫话机器学习系列】240.真正类率(True Positive Rate,TPR)
理解真正类率(True Positive Rate,TPR):公式、意义与应用
在机器学习与深度学习模型评估中,"真正类率"(True Positive Rate,简称TPR)是一个非常重要的指标。TPR反映了分类器对正样本识别能力的强弱,也常常被称为召回率(Recall)或灵敏度(Sensitivity)。
今天我们通过一张非常直观的图片,来深入理解TPR的定义、公式推导、实际应用场景,并探讨其与其他评估指标的关系。
什么是真正类率(TPR)?
真正类率(TPR) 衡量的是模型对实际为正的样本识别正确的比例。
直观地讲,它回答了这样一个问题:
在所有真实为正的样本中,有多少被正确地识别出来了?
如果一个模型能够将所有正样本都正确分类为正,那么它的TPR就是100%。
TPR的数学公式
根据上面提供的图片,TPR的公式可以写成:
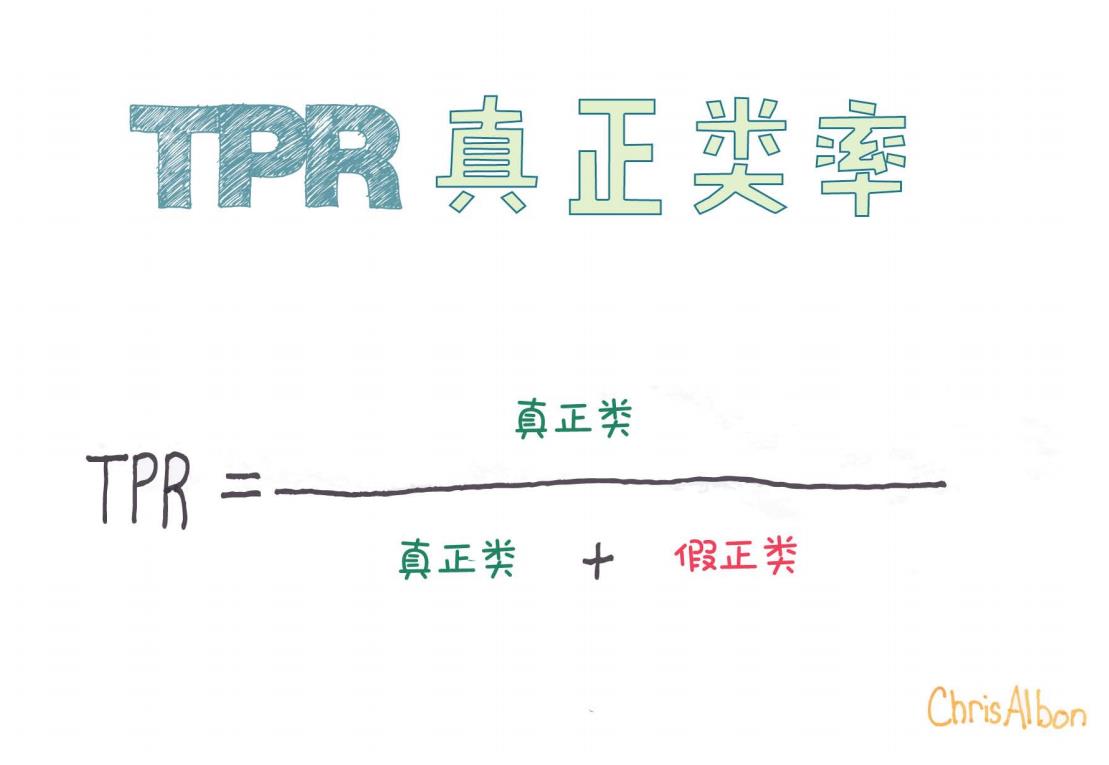
TPR=真正类真正类+假负类\text{TPR} = \frac{\text{真正类}}{\text{真正类} + \text{假负类}}
但是,图片里公式写成了另一种变形,稍有误导。让我们来细致地拆解一下:
-
真正类(True Positive,TP):模型正确预测为正的样本数量。
-
假负类(False Negative,FN):实际为正但被错误预测为负的样本数量。
因此标准的TPR公式应该是:

图片中提到的“假正类”其实是False Positive(FP),应该注意区分。
如果按照图片的公式(真正类 / (真正类 + 假正类)),其实描述的是**精准率(Precision)**而不是TPR。
所以,总结:真正类率(TPR)= 真正类 / (真正类 + 假负类)。
✅ 正确的TPR公式是基于假负类而不是假正类!
为什么TPR很重要?
在某些应用场景中,漏掉真正的正样本是非常严重的错误。例如:
-
疾病检测:将一个患病患者预测为健康(假负类)可能导致严重后果。
-
欺诈检测:漏掉一个真实欺诈行为(假负类)可能带来经济损失。
-
安全检查:漏检危险品可能导致安全事故。
因此,在这些场景中,我们希望TPR尽可能高,确保真正的正样本都能被识别出来。
举个例子
假设我们做了一个癌症检测模型,检测了100个病人,真实情况如下:
-
30个病人确实患有癌症(正样本)。
-
70个病人没有癌症(负样本)。
模型的预测结果:
-
成功检测出25个患癌者(True Positive = 25)。
-
漏掉5个患癌者,误判为健康(False Negative = 5)。
那么TPR就是:
即,模型的真正类率是83.33%,意味着83.33%的癌症患者被成功检测出来了。
TPR与其他指标的关系
在模型评估中,TPR通常不会单独使用,而是和其他指标一起分析,比如:
| 指标 | 公式 | 含义 |
|---|---|---|
| 精准率(Precision) | 预测为正的样本中,正确的比例 | |
| 召回率(Recall/TPR) | 实际为正的样本中,预测正确的比例 | |
| F1分数(F1 Score) | 综合考虑精准率和召回率 |
通常在精度(Precision)和召回率(Recall)之间存在权衡:
-
提高召回率,可能会降低精准率;
-
提高精准率,可能会降低召回率。
因此,实际应用中要根据业务需求选择最合适的指标。
总结
-
TPR(True Positive Rate)也叫召回率(Recall)或灵敏度(Sensitivity)。
-
正确公式是:TPR = 真正类 / (真正类 + 假负类)。
-
TPR用于衡量模型正确识别正样本的能力。
-
在医疗、金融安全等领域,TPR至关重要。
希望通过这篇文章,你对TPR有了更系统深入的理解!
附录:错误提示
⚠️ 图片中使用了“假正类(False Positive)”来计算TPR,这在严谨的定义中是错误的。
正确的TPR公式应该涉及假负类(False Negative)。
大家在学习过程中,务必注意区分**假正类(FP)和假负类(FN)**的不同概念哦!
如果你觉得这篇文章对你有帮助,欢迎点赞收藏!如果有疑问或者想继续了解其他评估指标(比如ROC曲线、AUC指标等),可以在评论区告诉我~
