当前位置：首页 > news >正文

Matlab实现基于CNN-GRU的锂电池SOH估计

news 来源：原创 2025/5/7 9:14:16

Matlab实现基于CNN-GRU的锂电池SOH估计

效果一览

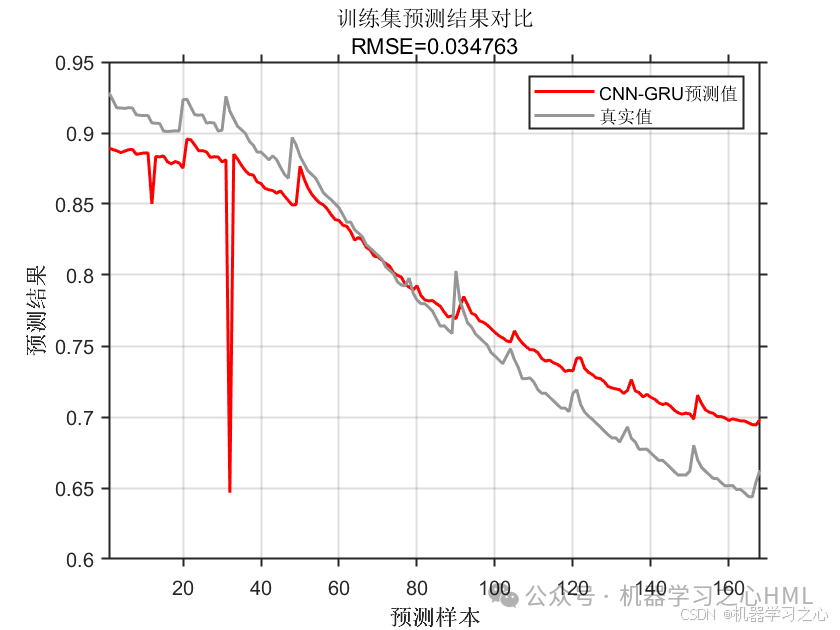
在这里插入图片描述

基本介绍

锂电池SOH估计！基于CNN-GRU的锂电池健康状态估计。CNN-GRU模型通过融合局部特征提取与长期依赖建模，显著提升了锂电池SOH估计的精度。其关键在于合理设计网络层次、优化特征工程策略，并结合实际应用场景选择评估指标。
数据来源：获取锂电池数据集（如NASA 数据集），包含电压、电流、温度、容量等时序数据。
特征选择：选取与SOH相关的特征（如电压曲线、电流曲线、温度变化等）。
数据归一化：对特征进行归一化（缩放到[0,1]），消除量纲影响。
锂电池健康状态（State of Health, SOH）是衡量电池性能退化程度的核心指标，通常以容量衰减率或内阻增加率表示，范围从0%（完全失效）到100%（全新状态）。其重要性体现在：
安全与效率：SOH直接影响电池的剩余寿命、充放电策略和热失控风险。例如，SOH低于80%的电池可能需退役。
经济性：在储能电站和电动汽车中，SOH评估可优化电池更换周期，降低运维成本。
可持续性：通过SOH监测实现梯次利用，减少资源浪费。
CNN-GRU混合模型结合了两种网络的互补特性：
CNN的局部特征提取
通过一维卷积核捕捉充放电数据中的局部模式（如电压曲线的拐点、温度波动）。
参数共享机制降低过拟合风险，适用于高维度传感器数据（电压、电流、温度等）。
GRU的时序依赖性建模更新门和重置门动态调整记忆单元，解决传统RNN的梯度消失问题。
对电池老化过程中的长期退化趋势（如容量随循环次数的非线性衰减）具有更强的捕捉能力。
三、模型架构设计
典型CNN-GRU混合模型包含以下核心模块：

输入层：接收多维度时序数据（如电压、电流、温度序列）。
CNN特征提取层
卷积层：使用多个滤波器提取局部特征，如充放电曲线的斜率变化。
池化层：通过最大池化降低数据维度，保留关键特征。
GRU时序建模层
将CNN输出的特征序列输入GRU，学习时间依赖性。例如，捕捉容量衰减与循环次数间的非线性关系。
输出层：全连接层映射到SOH值。
在这里插入图片描述

程序设计

完整源码私信回复Matlab实现基于CNN-GRU的锂电池SOH估计

%% 参数设置
options = trainingOptions('adam', ...     % Adam 梯度下降算法'MaxEpochs', 100,...                  % 最大训练次数'MiniBatchSize',64,...                % 批处理'InitialLearnRate', 0.001,...         % 初始学习率为0.001'L2Regularization', 0.001,...         % L2正则化参数'LearnRateSchedule', 'piecewise',...  % 学习率下降'LearnRateDropFactor', 0.1,...        % 学习率下降因子 0.1'LearnRateDropPeriod', 50,...         % 经过50次训练后 学习率为 0.001*0.1'ValidationPatience', Inf,...         % 关闭验证'Plots', 'training-progress',...      % 画出曲线'Verbose', false);
%%  训练模型
net= trainNetwork(p_train, t_train, lgraph, options);
%% 预测
t_sim1 = predict(net, p_train); 
t_sim2 = predict(net, p_test ); 
%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);
%%  相关指标计算
%  R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test  - T_sim2')^2 / norm(T_test  - mean(T_test ))^2;
disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])
%  MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;
disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1')./T_train));
MAPE2 = mean(abs((T_test - T_sim2')./T_test));
disp(['训练集数据的MAPE为：', num2str(MAPE1)])
disp(['测试集数据的MAPE为：', num2str(MAPE2)])
%  MBE
mbe1 = sum(abs(T_sim1' - T_train)) ./ M ;
mbe2 = sum(abs(T_sim1' - T_train)) ./ N ;
disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])