当前位置：首页 > news >正文

【模型量化】量化基础

news 来源：原创 2025/5/1 9:28:13

一、认识量化

二、量化基础原理

2.1 对称量化和非对称量化

2.1.1 对称量化

2.1.2 非对称量化

2.1.3 量化后的矩阵乘

2.2 神经网络量化

2.2.1 动态量化

2.2.2 静态量化

2.3 量化感知训练

一、认识量化

量化的主要目的是节约显存、提高计算效率以及加快通信

deepseek-r1-7b 模型以不同数值类型加载随不同数据类型所占用的显存大小也完全不一样，int4 数值类型加载仅需 fp32 加载的 1/8 的显存。通过量化技术能够把模型里的浮点数参数转化为低精度的整数参数，以此实现参数压缩。这不但能够削减模型所需的存储空间，还能缩短模型加载耗时

	FP32	FP16	INT8	INT4
显存占用	28G	14G	7G	3.5G

量化就是把Float类型（FP32、FP16）的模型参数和激活值（分别对应参数量化、激活值量化），用整数（INT8、INT4）来代替

同时需要尽可能减少量化后模型推理的误差。可以来一些好处：

减少模型的存储空间和显存的占用
减少显存和Tensorcore之间的数据传输量，从而加快模型推理时间
显卡对整数运算速度快于浮点型数据。从而加快模型推理时间

二、量化基础原理

量化就是使 $x_{f} \rightarrow x_{q}$ （量化）、 $x_{q} \rightarrow x_{f^{'}}$ （反量化），同时 $x_{f}$ 和 $x_{f^{'}}$ 要尽可能的接近

2.1 对称量化和非对称量化

2.1.1 对称量化

对称量化的原理就是找到 $x_{f}$ 中绝对值的最大值，然后对其进行缩放得到量化后的值，然后进行反量化得到原来的值，可以看出量化是存在一定误差的

这样量化的缺点就是，可能会有数值映射空间被浪费（ $x_{f}$ 中最大值对应映射空间的最大值，但最小值不对应映射空间最小值。如上图，最小值为-92，-93 ~ -127这段空间被浪费）。为了让量化后的数值空间被充分利用，引入非对称量化

2.1.2 非对称量化

非对称量化有一个额外的参数Z调整零点的映射，这个参数通常称为零点。非对称量化表示的范围没有严格的限制，可以根据浮点值的范围，选取任意的想要表示的范围。因此非对称量化的效果通常比对称量化好，但需额外存储以及推理时计算零点相关的内容

对称量化具有计算简单，精度低等特点，非对称量化的计算有一个额外的参数Z调整零点的映射，因此计算复杂，但精度相对较高

2.1.3 量化后的矩阵乘

下图为对称量化在居中乘法当中的应用示意图（非对称量化也类似），通过量化，将浮点矩阵的乘法，转化为整数矩阵的乘法，虽然存在一定误差，但误差不大。在矩阵乘法中采用量化可以降低计算复杂度，提升矩阵乘法效率

N * N 的矩阵，量化前共有 $N^{2}$ 次浮点数计算，量化后有 $N^{2}$ 次整型计算、N次浮点数与整型计算、一次浮点数计算。看似计算次数增多，整型数据在计算速度与传输速度上都大于浮点数

2.2 神经网络量化

为什么量化不会损失太多精度？

因为一般权重和输入都经过 Normalization，基本数值范围都不大
激活函数，数值影响会被平滑
对于绝大部分分类神经网络，最后都是概率值，只要最后某种类别概率高于其他类别就可以，不需要绝对数值准确

量化在神经网络中的是对每一层而言，每一层进行量化计算，每一层输出时进行反量化。具体而言，量化在神经网络中的应用又可分为动态量化（Post Training Quantization Dynamic, PTQ Dynamic）与静态量化（Post Training Quantization Static, PTQ Static）

2.2.1 动态量化

在模型推理过程中动态计算量化参数，仅量化权重，激活值在推理时动态量化。通常适用于Transformer、RNN、LSTM等

仅对权重（Weights）进行量化，激活保持 FP32
不需要标定数据

量化流程

将训练好的模型权重量化为INT8，并保存量化参数
在模型推理时，对每一层输入的FP32激活值，动态进行进行量化为INT8
在每一层对量化后的INT8权重和INT8激活值进行计算
在每一层输出时将结果反量化为FP32
将FP32激活值传入到下一层

直接使用 torch.quantization.quantize_dynamic() 来实现量化操作即可，量化需要在CPU中完成，所以需要把设备信息设置为CPU

import torch
import torch.nn as nnclass Model(nn.Module):def __init__(self):super(Model, self).__init__()self.linear1 = nn.Linear(768, 512)self.linear2 = nn.Linear(512, 314)self.linear3 = nn.Linear(314, 128)self.linear4 = nn.Linear(128, 64)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid()def forward(self, data):data = self.linear1(data)data = self.relu(data)data = self.linear2(data)data = self.relu(data)data = self.linear3(data)data = self.relu(data)data = self.linear4(data)data = self.sigmoid(data)return datadef main():torch.manual_seed(100)data = torch.randn(4, 768)# 量化前推理model = Model()output1 = model(data)print(output1)# 量化模型quantized_model = torch.quantization.quantize_dynamic(model, {torch.nn.Linear}, dtype=torch.qint8)# 量化后推理output2 = quantized_model(data)print(output2)# 模型保存torch.save(model, "./model")torch.save(quantized_model, "./quantized_model")if __name__ == "__main__":main()

调用 PyTorch 的 quantize_dynamic 函数对模型进行动态量化。指定量化 torch.nn.Linear 类型的层，将权重量化为 torch.qint8 类型，得到量化后的模型 quantized_model

模型中的所有 Linear 层变成了 DynamicQuantizedLinear 层

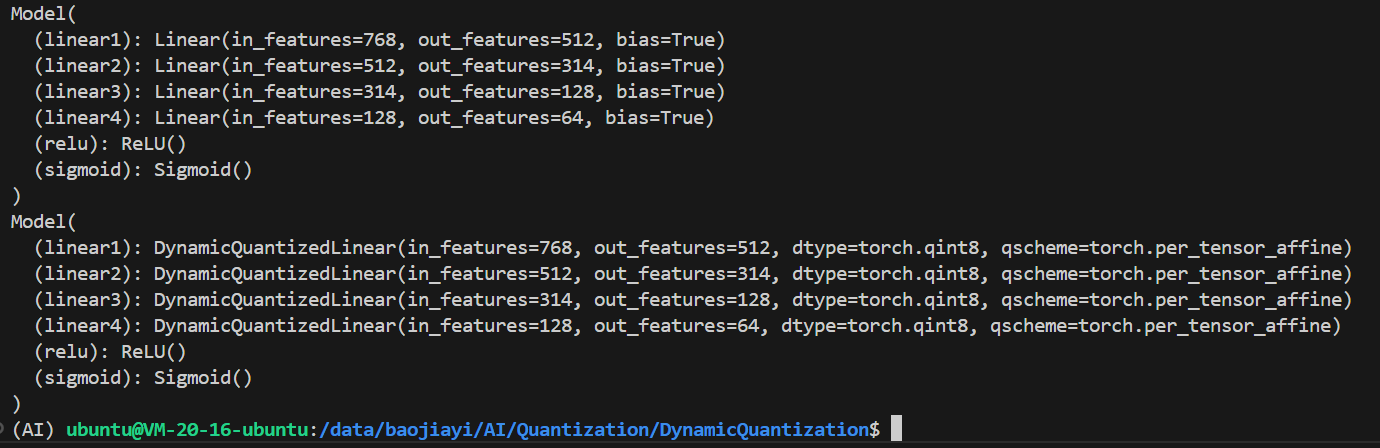
量化前后的模型输出会有一定差异，在实际使用中需要进行评估

tensor([[0.5179, 0.5051, 0.4849, 0.5051, 0.4962, 0.5127, 0.4963, 0.5223, 0.4858,0.5173, 0.4973, 0.4957, 0.4949, 0.4768, 0.5024, 0.4924, 0.4922, 0.5089,0.4982, 0.5187, 0.5301, 0.5003, 0.4945, 0.4974, 0.5036, 0.4974, 0.4658,0.4953, 0.5032, 0.5247, 0.4908, 0.5290, 0.4965, 0.5145, 0.4883, 0.5193,0.4864, 0.4947, 0.4970, 0.5083, 0.5006, 0.4734, 0.5016, 0.4797, 0.5154,0.5057, 0.5040, 0.4682, 0.5352, 0.5256, 0.4836, 0.5180, 0.4835, 0.4852,0.4819, 0.4781, 0.5027, 0.5042, 0.5164, 0.4814, 0.4754, 0.5106, 0.4996,0.5029],[0.5113, 0.5056, 0.4846, 0.5065, 0.4973, 0.4976, 0.4927, 0.5228, 0.4896,0.5117, 0.4979, 0.5049, 0.4964, 0.4696, 0.5109, 0.4985, 0.5010, 0.5215,0.5086, 0.5067, 0.5211, 0.5040, 0.4869, 0.4992, 0.5084, 0.5005, 0.4787,0.4884, 0.5010, 0.5216, 0.4869, 0.5285, 0.5032, 0.5114, 0.4842, 0.5166,0.4952, 0.4936, 0.5116, 0.5120, 0.4992, 0.4769, 0.5055, 0.4885, 0.5158,0.5016, 0.5039, 0.4801, 0.5199, 0.5355, 0.4835, 0.5116, 0.4831, 0.4764,0.4839, 0.4875, 0.5008, 0.4939, 0.5186, 0.4934, 0.4857, 0.5133, 0.5041,0.5088],[0.5060, 0.4920, 0.4859, 0.5196, 0.4865, 0.4944, 0.4927, 0.5032, 0.4783,0.5114, 0.5037, 0.5060, 0.5006, 0.4747, 0.4914, 0.4853, 0.4866, 0.5140,0.5123, 0.5206, 0.5369, 0.4999, 0.5022, 0.4968, 0.5095, 0.4960, 0.4667,0.4771, 0.4929, 0.5121, 0.4905, 0.5138, 0.5042, 0.5163, 0.4904, 0.5030,0.4818, 0.4835, 0.4928, 0.5165, 0.5134, 0.4696, 0.4991, 0.4817, 0.5264,0.5011, 0.4912, 0.4741, 0.5414, 0.5255, 0.4847, 0.5115, 0.4963, 0.4668,0.4893, 0.4925, 0.4882, 0.5030, 0.5091, 0.4816, 0.4877, 0.5033, 0.4960,0.5164],[0.5186, 0.4994, 0.4805, 0.5198, 0.4900, 0.4988, 0.4904, 0.5132, 0.4820,0.5176, 0.5004, 0.5027, 0.4984, 0.4646, 0.5005, 0.4931, 0.4922, 0.5190,0.5077, 0.5191, 0.5297, 0.5008, 0.4907, 0.4966, 0.5053, 0.5080, 0.4790,0.4849, 0.5159, 0.5269, 0.4804, 0.5240, 0.5023, 0.5079, 0.4939, 0.5178,0.4892, 0.4996, 0.5001, 0.5066, 0.4999, 0.4768, 0.4974, 0.4833, 0.5160,0.5086, 0.5015, 0.4754, 0.5317, 0.5420, 0.4927, 0.5129, 0.4932, 0.4706,0.4743, 0.4742, 0.4948, 0.5074, 0.5127, 0.4840, 0.4751, 0.5050, 0.4937,0.5095]], grad_fn=<SigmoidBackward0>)
tensor([[0.5185, 0.5053, 0.4851, 0.5046, 0.4961, 0.5130, 0.4963, 0.5226, 0.4856,0.5172, 0.4971, 0.4955, 0.4947, 0.4766, 0.5030, 0.4925, 0.4923, 0.5091,0.4986, 0.5187, 0.5297, 0.5004, 0.4943, 0.4972, 0.5033, 0.4974, 0.4658,0.4953, 0.5032, 0.5246, 0.4906, 0.5291, 0.4970, 0.5148, 0.4879, 0.5194,0.4863, 0.4949, 0.4967, 0.5085, 0.5010, 0.4734, 0.5017, 0.4797, 0.5159,0.5061, 0.5044, 0.4683, 0.5351, 0.5254, 0.4838, 0.5180, 0.4838, 0.4853,0.4821, 0.4779, 0.5027, 0.5046, 0.5162, 0.4814, 0.4750, 0.5106, 0.4993,0.5028],[0.5117, 0.5056, 0.4841, 0.5065, 0.4975, 0.4975, 0.4928, 0.5230, 0.4897,0.5118, 0.4982, 0.5047, 0.4963, 0.4697, 0.5111, 0.4988, 0.5008, 0.5218,0.5085, 0.5063, 0.5207, 0.5040, 0.4865, 0.4991, 0.5083, 0.5008, 0.4787,0.4887, 0.5011, 0.5217, 0.4867, 0.5284, 0.5036, 0.5114, 0.4844, 0.5164,0.4954, 0.4937, 0.5115, 0.5119, 0.4991, 0.4770, 0.5053, 0.4886, 0.5156,0.5018, 0.5041, 0.4802, 0.5199, 0.5357, 0.4837, 0.5113, 0.4827, 0.4762,0.4834, 0.4870, 0.5011, 0.4941, 0.5187, 0.4936, 0.4859, 0.5132, 0.5039,0.5088],[0.5062, 0.4918, 0.4858, 0.5190, 0.4866, 0.4945, 0.4927, 0.5030, 0.4787,0.5113, 0.5031, 0.5057, 0.5007, 0.4748, 0.4913, 0.4854, 0.4867, 0.5144,0.5122, 0.5206, 0.5371, 0.5000, 0.5022, 0.4967, 0.5097, 0.4959, 0.4666,0.4771, 0.4929, 0.5123, 0.4904, 0.5138, 0.5046, 0.5163, 0.4904, 0.5028,0.4816, 0.4833, 0.4927, 0.5167, 0.5137, 0.4695, 0.4992, 0.4816, 0.5264,0.5014, 0.4912, 0.4741, 0.5411, 0.5254, 0.4851, 0.5116, 0.4962, 0.4667,0.4894, 0.4923, 0.4883, 0.5032, 0.5092, 0.4813, 0.4878, 0.5030, 0.4961,0.5168],[0.5190, 0.4993, 0.4803, 0.5200, 0.4900, 0.4990, 0.4905, 0.5135, 0.4821,0.5172, 0.5004, 0.5026, 0.4980, 0.4645, 0.5009, 0.4930, 0.4923, 0.5193,0.5079, 0.5190, 0.5296, 0.5006, 0.4906, 0.4968, 0.5051, 0.5082, 0.4793,0.4848, 0.5156, 0.5268, 0.4804, 0.5241, 0.5025, 0.5077, 0.4939, 0.5179,0.4895, 0.4997, 0.5000, 0.5068, 0.5001, 0.4765, 0.4975, 0.4836, 0.5158,0.5087, 0.5017, 0.4753, 0.5316, 0.5416, 0.4925, 0.5126, 0.4932, 0.4707,0.4744, 0.4743, 0.4948, 0.5075, 0.5128, 0.4840, 0.4749, 0.5050, 0.4938,0.5095]])

完成动态量化后，模型的大小会得到缩小

训练后动态量化存在的问题：

每次推理时每层都要对输入统计量化参数（如：比例因子和零点），耗时
每层计算完都转化为FP32，存入显存，占用显存带宽

2.2.2 静态量化

针对动态量化的问题1：通过用有代表性的输入数据跑一遍整个网络，通过统计得到每层大概得量化参数来解决
问题2：这一层的输出是下一层的输入。下一层还是要量化，通过在这一层直接量化好再传给下一层方法来解决

静态量化流程如下：

将训练好的模型权重量化为INT8，并保存量化参数
校准(calibration)：利用一些有代表性的数据进行模型推理，用这些数据在神经网络每一层产生的激活估算出激活值的量化参数。这样就不用推理时每次根据实际激活值计算量化参数
在每一层对量化后的INT8权重和INT8激活值进行计算
在每一层输出时将结果反量化为FP32，同时根据校准产生的激活值量化参数，把激活值量化为INT8，把量化参数放入量化后的激活值中
将INT8的激活值和其量化参数传入到下一层

反量化+量化：反量化时用的是上一层的量化参数，量化时用的是本层的量化参数

具体实现

import torch
import torch.nn as nn
import torch.ao.quantization as quantizationclass Model(nn.Module):def __init__(self):super(Model, self).__init__()self.quant = quantization.QuantStub()self.dequant = quantization.DeQuantStub()self.linear1 = nn.Linear(768, 512)self.linear2 = nn.Linear(512, 314)self.linear3 = nn.Linear(314, 128)self.linear4 = nn.Linear(128, 64)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid()def forward(self, data):data = self.quant(data)data = self.linear1(data)data = self.linear2(data)data = self.dequant(data)data = self.relu(data)data = self.quant(data)data = self.linear3(data)data = self.dequant(data)data = self.relu(data)data = self.quant(data)data = self.linear4(data)data = self.dequant(data)data = self.sigmoid(data)return datadef main():torch.manual_seed(100)data = torch.randn(2, 768)# 量化前推理model = Model()output1 = model(data)print(output1)# 量化模型weight_observer = quantization.PerChannelMinMaxObserver.with_args(dtype=torch.qint8, qscheme=torch.per_channel_symmetric, quant_min=-128, quant_max=127)activation_observer = quantization.MinMaxObserver.with_args(dtype=torch.quint8, qscheme=torch.per_tensor_affine, quant_min=0, quant_max=255)qconfig = quantization.QConfig(activation=activation_observer,weight=weight_observer)model.qconfig = qconfigmodel_prepared = quantization.prepare(model)model_prepared(data)model_int8 = quantization.convert(model_prepared)# 量化后推理output2 = model_int8(data)print(output2)# 查看模型print(model)print(model_int8)print("int8 model linear1 parameter (int8):\n", torch.int_repr(model_int8.linear1.weight()))print("int8 model linear1 parameter:\n", model_int8.linear1.weight())# 模型保存torch.save(model, "./model")torch.save(model_int8, "./model_int8")if __name__ == "__main__":main()

量化有多个 qscheme，可以根据具体情况进行控制

2.3 量化感知训练

量化会存在误差。量化感知训练就是在网络训练过程中，模拟量化，让模型在训练过程中就能调整参数，让其更适合量化，提高量化后模型的精度

加载FP32的模型参数
输入FP32的激活值
通过在网络里插入模拟量化节点（fake_quantization）来分别对模型参数和激活值进行量化和反量化。从而引入量化误差
模型在FP32精度下进行计算
计算后的激活值传入下一层

import torch
import torch.nn as nn
import torch.ao.quantization as quantizationtorch.manual_seed(123)class Model(nn.Module):def __init__(self):super(Model, self).__init__()self.quant = quantization.QuantStub()self.dequant = quantization.DeQuantStub()self.linear1 = nn.Linear(768, 512)self.linear2 = nn.Linear(512, 314)self.linear3 = nn.Linear(314, 128)self.linear4 = nn.Linear(128, 64)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid()def forward(self, data):data = self.quant(data)data = self.linear1(data)data = self.linear2(data)data = self.dequant(data)data = self.relu(data)data = self.quant(data)data = self.linear3(data)data = self.dequant(data)data = self.relu(data)data = self.quant(data)data = self.linear4(data)data = self.dequant(data)data = self.sigmoid(data)return datadef main():torch.manual_seed(123)train_data = torch.randn(30000, 768)torch.manual_seed(123)train_label = torch.randn(30000, 64)model = Model()weight_observer = quantization.PerChannelMinMaxObserver.with_args(dtype=torch.qint8, qscheme=torch.per_channel_symmetric, quant_min=-128, quant_max=127)activation_observer = quantization.MinMaxObserver.with_args(dtype=torch.quint8, qscheme=torch.per_tensor_affine, quant_min=0, quant_max=255)qconfig = quantization.QConfig(activation=activation_observer,weight=weight_observer)model.qconfig = qconfigmodel_prepared = quantization.prepare_qat(model)optimizer = torch.optim.Adam(model_prepared.parameters(), lr=0.01)for i in range(10):preds = model_prepared(train_data)loss = torch.nn.functional.mse_loss(preds, train_label)loss.backward()optimizer.step()optimizer.zero_grad()print("loss:", i, loss)if __name__ == "__main__":main()

直接将准备量化感知训练模型 model_prepared = torch.ao.quantization.prepare_qat(model)，将量化参数视为可训练的，以此来降低损失