Transformer-CVPR2025-线性注意力-Breaking the Low-Rank Dilemma of Linear Attention

Transformer-CVPR2025-线性注意力-Breaking the Low-Rank Dilemma of Linear Attention

本工作提出了一个非常有意义的观点：线性注意力虽然高效，但其表达能力受限于“低秩”问题。为此，作者引入了“秩增强”机制，既保留了线性复杂度，又提升了建模能力，最终构建的 RAVLT 模型在 ImageNet 上表现优异，展示了线性注意力在视觉领域进一步发展的可能性。

论文链接：Breaking the Low-Rank Dilemma of Linear Attention
代码链接：qhfan/RALA

1.普通（Softmax）注意力和线性注意力

1.1 什么是普通（Softmax）注意力

在 Transformer 中，注意力的核心计算公式是：

解释一下这些符号：

• Q 是 Query（查询向量）
• K 是 Key（键向量）
• V 是 Value（值向量）
• QK^T 是一个 矩阵乘法，结果是个 n×n 的矩阵（如果输入是 n 个 token，比如图像有 n 个 patch）

这个公式中最耗费计算的就是：

它的计算量是 O(n²)，也就是输入长度的平方。想象一下如果有 1000 个 token，要算一个 1000x1000 的矩阵，这得多少次乘法和加法！所以计算量暴涨。

举例说明：

🧮 第一步：QK^T 的结果

我们有 4 个 token，每个维度是 2：

Q = [[1, 0],[0, 1],[1, 1],[0.5, 0.5]]K = [[1, 0],[0, 1],[1, 1],[1, -1]]

现在我们计算 QKT（4×2 × 2×4 → 得 4×4）：

QK^T =
[[1, 0] dot K[i] for i in 0~3] → [1, 0, 1, 1]   ← Q[0]
[[0, 1] dot K[i] for i in 0~3] → [0, 1, 1, -1]  ← Q[1]
[[1, 1] dot K[i] for i in 0~3] → [1, 1, 2, 0]   ← Q[2]
[[0.5, 0.5] dot K[i] for i in 0~3] → [0.5, 0.5, 1.0, 0.0] ← Q[3]结果矩阵（QK^T）：
[[1.0, 0.0, 1.0, 1.0],[0.0, 1.0, 1.0, -1.0],[1.0, 1.0, 2.0, 0.0],[0.5, 0.5, 1.0, 0.0]]

📈 第二步：每行做 Softmax

Softmax 的公式是：

我们来对每一行应用 softmax。

对第一行 [1.0, 0.0, 1.0, 1.0]：

所以：

Softmax → [2.718/9.154, 1/9.154, 2.718/9.154, 2.718/9.154] ≈ [0.297, 0.109, 0.297, 0.297]

第二行 [0, 1, 1, -1]：

Softmax ≈ [0.147, 0.399, 0.399, 0.054]

🔄 第三步：Softmax结果乘 V

V 是：

V = [[1, 1],[2, 2],[3, 3],[4, 4]]  # shape: 4x2

我们现在把每一行的 softmax 结果（是一个 1x4 向量）乘以 V（4x2），结果就是一个 1x2 向量，也就是每个 token 最终的输出。

举个例子：第一行的 Softmax 是 [0.297, 0.109, 0.297, 0.297]

乘以 V，就是：

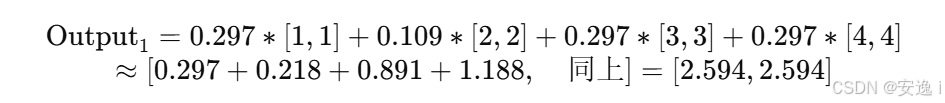
所以第一行输出是 [2.594, 2.594]。

每一行都这样乘一次，就能得到最终的 attention 输出。

✅ 总结这个过程

阶段	操作	复杂度
1️⃣ QKT	4×2 × 2×4 → 得 4×4	O(n²)
2️⃣ Softmax	每行归一化，共 n 行	O(n²)
3️⃣ 乘以 V	4×4 × 4×2 → 4×2	O(n²)

1.2 那么“线性注意力”是怎么优化的？

关键点是：

它 不先计算 QK^T，而是用一个数学技巧把它重新组织成一组“线性计算”。

原理上，它把 Attention 写成一个变形的公式，比如下面这种形式（不同方法有不同的变形）：

这个好处是：

• 把原来 n×n 的计算，变成了 n×d 和 d×d 的计算，复杂度变成了 O(n)。
• 你可以提前先算好 K^T V 这个值，不用每次重新计算。

这种技巧叫做“因式分解 attention”或者“核技巧（kernel trick）”，本质就是通过数学重写，避免了那个大矩阵 QK^T 的直接计算。

举例说明：（4 个 token，d=2）

Softmax Attention 的瓶颈在于要算 Q @ K^T，这是一个 n × n 的矩阵（n 是 token 数），所以是 O(n²)。

线性注意力 的核心思路是：
将注意力公式变形，把 Softmax(Q @ K^T) 改为 φ(Q) @ (φ(K)^T @ V)，其中 φ 是一个激活函数（如 ReLU、ELU、或者线性核），并巧妙地调换矩阵乘法的顺序，从而避免了 n × n 的计算。

Q = [[1, 0],[0, 1],[1, 1],[0.5, 0.5]]K = [[1, 0],[0, 1],[1, 1],[1, -1]]V = [[1, 1],[2, 2],[3, 3],[4, 4]]

我们选择一个简单激活函数：φ(x) = x（即恒等函数，不变形，便于演示）

🧮 具体演算步骤

Step 1：先计算 K' = φ(K) 和 Q' = φ(Q)

我们这里 φ 是恒等函数，所以 K' = K，Q' = Q。

Step 2：计算 中间项 K'^T @ V（这里是 2x4 × 4x2 → 得 2x2）

K.T = [[1, 0, 1, 1],   # 第一列[0, 1, 1, -1]]  # 第二列V = [[1, 1],[2, 2],[3, 3],[4, 4]]

计算：

• 第一行 dot V 第一列：

​ 1×1+0×2+1×3+1×4=1+0+3+4=8

• 第一行 dot V 第二列（同上）也是 8
• 第二行 dot V 第一列：

​ 0×1+1×2+1×3+(−1)×4=2+3−4=10
得到：

K^T @ V = [[8, 8],[1, 1]]

Step 3：计算最终输出：Q @ (K^T @ V)，也就是 4x2 × 2x2 → 4x2

Q = [[1, 0],[0, 1],[1, 1],[0.5, 0.5]]K^T @ V = [[8, 8],[1, 1]]

✅ 最终输出：

[[8.0, 8.0],[1.0, 1.0],[9.0, 9.0],[4.5, 4.5]]

🚀 复杂度分析对比

方式	核心操作	复杂度
Softmax Attention	Q × KT (n×n)	O(n²)
Linear Attention	KT × V (d×d)，再 Q × …	O(n)

1.3 🧠通俗比喻

想象你要把 100 个学生的身高两两配对，计算他们身高差的平均值：

• 原来的方法是，100人之间两两配对，共需要算 4950 次差值（就像 QK^T 那样的 n² 复杂度）。
• 线性注意力的做法是，先把所有人分成几组，然后组内先做统计（比如平均身高），最后再用这些汇总数据来近似整个配对结果，这样只要做几十次计算。

虽然信息量稍微有点损失，但速度大大提升了。

2 .本文主要创新点

1️⃣ 问题发现：线性注意力性能下降的根本原因

• 作者指出，线性注意力机制性能下降的主要原因是其输出特征图呈**低秩（low-rank）**特性，导致无法充分捕捉复杂的空间信息；
• 这不同于以往仅从效率角度讨论线性注意力的研究，作者是从特征表达能力的维度挖掘问题本质。

2️⃣ 解决思路：从两个角度做秩分析

• 作者从 两个关键视角（KV缓存层（KV buffer） 和 输出特征图）出发，进行了系统的秩分析；
• 这一步是理论基础，揭示了低秩的来源并为改进提供方向。

3️⃣ 方法创新：提出 Rank-Augmented Linear Attention（RALA）

• 设计了一种新的注意力机制——RALA，其核心目标是：
  • 在保持线性计算复杂度的同时，
  • 提升注意力输出的秩，增强模型的表达能力；

2.1 低秩（low-rank）特性是什么?

🎯 什么是“秩”（Rank）？

在数学中，秩描述的是一个矩阵中信息的丰富程度。

• 举个简单的例子，一个矩阵可以被看作由若干个向量组合而成；
• 如果这些向量中很多彼此线性相关（也就是你能用几个向量“拼出”其他的），那么这个矩阵就“没那么丰富”——也就是说，它是低秩的；
• 相反，如果向量之间彼此独立，那么矩阵就高秩，包含更多元、复杂的信息。

🧠 低秩的“通俗比喻”

可以想象成一个“图书馆”：

• 高秩图书馆里，书的种类丰富，既有科技类也有文学类、历史类等；
• 低秩图书馆里虽然也有很多书，但它们可能只是同一本书的不同版本，信息非常重复，内容很单一。

在视觉任务中，我们希望注意力机制输出的特征图能“像高秩图书馆”一样，能表达丰富多样的空间信息（比如边缘、纹理、形状、细节等）。

2.1 为什么线性注意力容易“低秩”？

线性注意力（Linear Attention） 通常将其重写为：

其中：

• ϕ(⋅)是一个激活函数或核映射函数，比如 ReLU、ELU，或者 Softmax 的近似形式；
• 这个公式先计算 ϕ(K)⊤⋅V，这是一个固定的值（与每个 Q 无关）；
• 然后再让每个 ϕ(Q) 与它相乘。

❗问题出在哪？

注意这里的顺序：

• ϕ(K)⊤⋅V 是一个 全局聚合后的向量或矩阵；

• 然后再与每个 ϕ(Q)\phi(Q)ϕ(Q) 相乘，就意味着：

  “所有 Query 都用同一个经过压缩的信息来生成输出”。

这就相当于你把整张图的信息提前“捏成一团”，然后用这团东西去产生所有注意力结果。结果就是：

• 所有输出都从一个相似的源出发；
• 导致输出特征矩阵秩（rank）变低；
• 模型最终难以表达复杂的细节结构。

3.代码如何解决 低秩（low-rank）问题？

原代码如下：

class GateLinearAttentionNoSilu(nn.Module):def __init__(self, dim, num_heads):super().__init__()self.dim = dimself.num_heads = num_headsself.head_dim = dim // num_headsself.scale = self.head_dim ** (-0.5)self.qkvo = nn.Conv2d(dim, dim * 4, 1)self.elu = nn.ELU()self.lepe = nn.Conv2d(dim, dim, 5, 1, 2, groups=dim)self.proj = nn.Conv2d(dim, dim, 1)def forward(self, x: torch.Tensor, sin: torch.Tensor, cos: torch.Tensor):'''x: (b c h w)sin: ((h w) d1)cos: ((h w) d1)'''B, C, H, W = x.shapeqkvo = self.qkvo(x)  # (b 3*c h w)qkv = qkvo[:, :3 * self.dim, :, :]o = qkvo[:, 3 * self.dim:, :, :]lepe = self.lepe(qkv[:, 2 * self.dim:, :, :])  # (b c h w)q, k, v = rearrange(qkv, 'b (m n d) h w -> m b n (h w) d', m=3, n=self.num_heads)  # (b n (h w) d)q = self.elu(q) + 1.0k = self.elu(k) + 1.0  # (b n l d)q_mean = q.mean(dim=-2, keepdim=True)  # (b n 1 d)eff = self.scale * q_mean @ k.transpose(-1, -2)  # (b n 1 l)eff = torch.softmax(eff, dim=-1).transpose(-1, -2)  # (b n l 1)k = k * eff * (H * W)q_rope = theta_shift(q, sin, cos)k_rope = theta_shift(k, sin, cos)z = 1 / (q @ k.mean(dim=-2, keepdim=True).transpose(-2, -1) + 1e-6)  # (b n l 1)kv = (k_rope.transpose(-2, -1) * ((H * W) ** -0.5)) @ (v * ((H * W) ** -0.5))  # (b n d d)res = q_rope @ kv * z  # (b n l d)res = rearrange(res, 'b n (h w) d -> b (n d) h w', h=H, w=W)res = res + lepereturn self.proj(res * o)

下面详解解释代码中的五个特性

🧩 3.1门控机制（Gating）增强输出表达能力

📌 原理：

在标准线性注意力中，输出为 Attention = Q @ (Kᵗ @ V)，这个输出是直接由注意力机制给出的。然而，它的表达空间受限于 KV 之间的全局压缩结构，无法单独调节每个通道或位置的重要性。

引入 O（门控项），使得最终输出为：

这里 O 是通过网络学习得来的“控制门”，类似于 LSTM 中的“门”或 SENet 中的“通道注意力”。

🧠 直觉理解：

你把注意力模块当成“讲课内容”，而 O 是“麦克风音量控制器”——不同通道（信息维度）可以通过 O 来“调大”或“调小”自己的输出，不再受注意力矩阵的单一决定。

🪄 举例：

假设注意力计算出了三个通道输出分别为 [2, 5, 1]，而 O 输出为 [0.5, 1.0, 2.0]，则最终输出为：

​ [2×0.5,5×1.0,1×2.0]=[1,5,2]

更高效地区分通道贡献，提升了表示能力，避免信息被平均压平（低秩）。

🧩3.2 LEPE（Local Enhancement Positional Encoding）弥补局部感知缺失

📌 原理：

由于线性 attention 是基于全局聚合的，不容易建模局部空间结构。LEPE 使用 depthwise 卷积（5×5）对 V 的表示进行局部增强，像 CNN 一样引入局部感知偏置。

最终形式是：

🧠 直觉理解：

Attention 像是从“全局信息”中找关键点；而卷积像是从“邻居”中找相关性。两者结合才能又看全局又看细节。

🪄 举例：

假设一张图中有“猫眼睛”，全局注意力可能会看整个猫脸，忽视眼睛的局部形状；加了 LEPE 后，就像用 5x5 小窗扫描眼睛周围的细节，防止局部特征被“平均掉”。

🧩 3.3 Query 均值引导的 Key 加权：避免一锅端地压缩

📌 原理：

传统线性 attention 中，Kᵗ @ V 对所有位置聚合，所有 query 使用的是一个“全局压缩后的 KV 语义”。
这会导致表达能力过于集中，输出秩变低。

本模块中，先计算 Query 的均值，然后用它去加权所有 Key 的重要性，计算形式如下：

这相当于告诉网络：“我平均地问一遍‘你们谁重要’，再按重要程度重新组织 Key”。

🧠 直觉理解：

就像老师要总结全班的发言，不是随机选几个，而是先听所有人，然后根据“代表性发言”（Query 均值）给每个人打权重，决定听谁的多、谁的少。

🪄 举例：

如果一张图的 Query 平均语义是“左边亮、右边暗”，那这个机制就会给右边的 Key 赋予更多权重，帮助表达出这种空间异质性。

🧩 3.4 RoPE（旋转位置编码）增强空间结构感知

📌 原理：

线性 attention 缺乏位置信息，因为它是全连接、全局加权的。RoPE（Rotary Positional Encoding）通过将位置作为相位角加入到 Q/K 中，使得位置以旋转相位的方式编码。

效果类似于：

🧠 直觉理解：

你可以把 Q/K 看作坐标轴上的向量，RoPE 让每个位置上的向量都按照位置进行旋转，让模型能知道“这是谁说的”。

🪄 举例：

假设有两个 token：“猫在左边”和“猫在右边”，原 attention 可能只看到“猫”；加了 RoPE 后，“猫”左边和右边的位置角度不同，模型就能分辨出空间结构了。

🧩 3.5 注意力归一化与缩放（z 和 1/√HW）

📌 原理：

线性 attention 会把 K 和 V 做全局压缩，为防止值爆炸，需引入缩放项。这里的缩放形式是：

这种缩放方式类似 Softmax 的 scale 控制，但更加精细地控制注意力分布的动态范围，防止某些通道 dominate 全部表示。

🧠 直觉理解：

好比老师分配 100 分，不能全给一个学生，要控制范围，避免资源极度倾斜。

🪄 举例：

如果有一张图中某个像素的注意力特别强，没有缩放控制就会导致整个输出由它决定，其他特征被压平。这正是低秩问题的源头之一。

✅ 总结

方法	解决的问题	本质机制	通俗举例
门控机制 O	增强通道表达	res × o	每个通道开/关麦克风调音
LEPE 局部增强	弥补空间感知缺失	5x5 DW Conv	局部扫描补细节
Query 引导加权	缓解全局压缩损失	eff = softmax(q_mean × kᵗ)	汇总大家意见决定权重
RoPE 位置编码	引入空间结构感知	q = theta_shift(q)	不同位置编码旋转角度
注意力归一化	控制注意力值爆炸	z = 1 / (…), √HW	给每个值“掂量掂量份量”