当前位置：首页 > wzjs >正文

dede 企业网站模板下载电视剧百度搜索风云榜

wzjs 2025/7/20 15:53:36

dede 企业网站模板下载,电视剧百度搜索风云榜,平湖市规划建设局网站,渠道网络股份有限公司时间线 8:30 ~ 10:00 设计 T1 的状态、推转移式、对着一个不存在的错误虚空思考然后过了。10:00 ~ 10:30 推 T2 的式子，然后坠机了没推出来。10:30 ~ 12:00 推推 T2 式子、想想 T3 能不能用可持久化线段树做，无果。最后时刻发现 T3 暴力没加强制在线&…

时间线

8:30 ~ 10:00 设计 T1 的状态、推转移式、~~对着一个不存在的错误虚空思考~~然后过了。
10:00 ~ 10:30 推 T2 的式子，然后坠机了没推出来。
10:30 ~ 12:00 推推 T2 式子、想想 T3 能不能用可持久化线段树做，无果。
最后时刻发现 T3 暴力没加强制在线（

成绩

题解

T1

给定一个长度为 $n$ 数列 $A$ 和两个非负常数 $a, b$ ，你需要进行若干次操作，每次选定 $A$ 中的一段区间 $[l, r]$ ，删除这段区间并把剩下的部分按照原顺序连接起来，代价是 $a+b(max⁡i=lrAi−min⁡i=lrAi)2a+b\left(\max_{i=l}^r A_i-\min_{i=l}^rA_i\right)^2$ ；求将 $A$ 删空的最小代价。

$n≤50n\le 50$ ， $a≤1500a\le 1500$ ， $b≤10b\le 10$ ， $0≤Ai≤10000\le A_i\le 1000$ 。

不妨把每次操作放到原序列上看看长什么样。

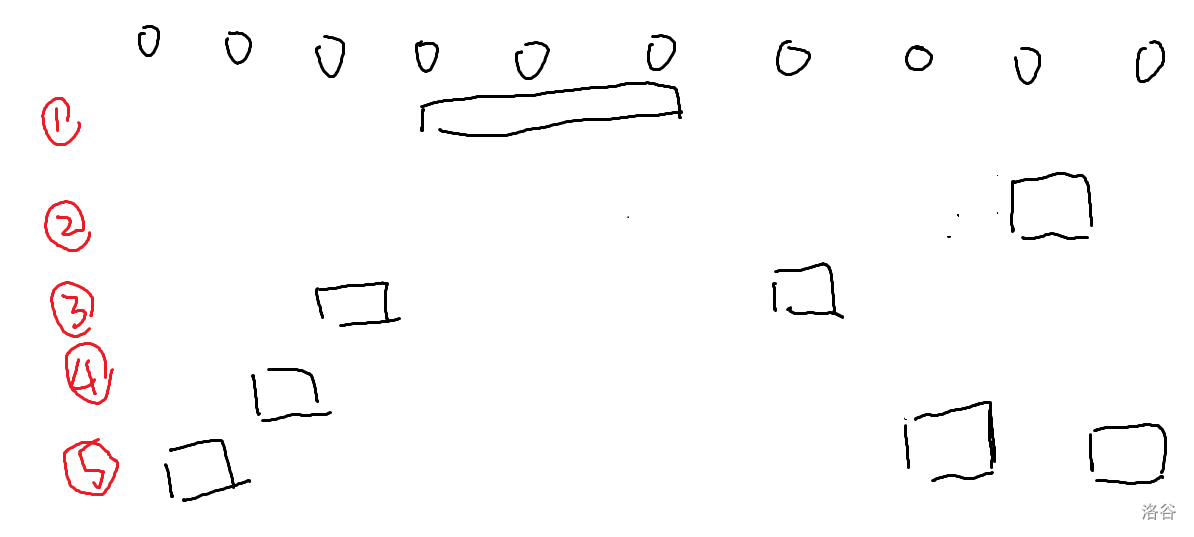
可以发现，每次操作在原序列上形如：选定若干段区间，放在一起计算代价，且选定的区间不能有相交的情况。考虑 dp，设 $f (l, r, m x, mn)$ 表示把 $A [l : r]$ 的部分删空，且最后的一步删掉了 $l, r$ 两个位置的元素，最后删除的若干段区间 $max⁡\max$ 为 $m x$ ， $min⁡\min$ 为 $mn$ （可以改成记录 $m x, mn$ 在的位置）；且没有算上最后一次删除的代价（方便合并）。转移的时候从短到长枚举 $[l, r]$ ，考虑 $A_r$ 怎么删掉，枚举一个 $mi d$ 表示 $r$ 和 $[l, mi d]$ 一起删掉，那么 $[mi d + 1, r - 1]$ 的部分就独立出来了。此时该代价可以贡献到 $f(l,r,\max(mx,A_r),\min(mn,A_r))$ ，代价为
$min_{mid=l}^{r-1}f(l,mid,mx,mn)+g(mid+1,r-1)$
其中 $g (mi d + 1, r - 1)$ 表示单纯把 $[mi d + 1, r - 1]$ 删掉的情况。现在考虑算 $g (l, r)$ ，一种就是所有 $f (l, r, X, Y)$ 的 $min⁡\min$ ；也可以不是一步删完，即枚举 $mid∈[l,r−1]mid\in[l,r-1]$ ，取 $g (l, mi d) + g (mi d + 1, r)$ 的 $min⁡\min$ 。时间复杂度 $O(n^5)$ 。

const int maxn = 55;
int A[maxn], a, b, n;
ll f[maxn][maxn][maxn][maxn];
// 解决 [l, r]，最大值取在 i 上，最小值取在 j 上，没有结算
ll g[maxn][maxn];
// [l, r] 的答案
int getid_max(int i, int j) {return A[i] == A[j] ? i < j ? i : j : A[i] > A[j] ? i : j;
} int getid_min(int i, int j) {return A[i] == A[j] ? i < j ? i : j : A[i] < A[j] ? i : j;
}
int main() { // open(2);scanf("%d %d %d", &n, &a, &b);for (int i = 1; i <= n; i ++) scanf("%d", &A[i]);for (int i = 1; i <= n; i ++)for (int j = i, mx = A[i], mn = A[i], mx_id = i, mn_id = i; j <= n; j ++) {mx_id = getid_max(mx_id, j), mn_id = getid_min(mn_id, j);chkmax(mx, A[j]), chkmin(mn, A[j]);g[i][j] = a + 1ll * b * (mx - mn) * (mx - mn);for (int k = 1; k <= n; k ++)for (int t = 1; t <= n; t ++)f[i][j][k][t] = linf;f[i][j][mx_id][mn_id] = 0;}for (int i = 1; i <= n; i ++)f[i][i][i][i] = 0, g[i][i] = a;for (int len = 2; len <= n; len ++) for (int l = 1, r = l + len - 1; r <= n; l ++, r ++) {for (int mid = l; mid < r; mid ++)chkmin(g[l][r], g[l][mid] + g[mid + 1][r]);for (int i = l; i <= r; i ++)for (int j = l; j <= r; j ++) {int cur_i = getid_max(i, r), cur_j = getid_min(j, r);ll &cur = f[l][r][cur_i][cur_j];for (int mid = l; mid <= r - 1; mid ++)chkmin(cur, f[l][mid][i][j] + (mid == r - 1 ? 0 : g[mid + 1][r - 1]));chkmin(g[l][r], f[l][r][cur_i][cur_j] + a + 1ll * b * (A[cur_i] - A[cur_j]) * (A[cur_i] - A[cur_j]));}}printf("%lld\n", g[1][n]);return 0;
}

T2

给定 $n, m, k$ ，求
$\sum_{i=0}^m\binom{m}{i}\binom{n-m+2i}{k}$
对 $10^9+7$ 取模， $T$ 组数据。 $n,m≤109n,m\le 10^9$ ， $k≤103k\le 10^3$ ， $T≤100T\le 100$ 。

组合意义

相当于有 $n$ 个人和 $k$ 个任务，其中有 $m$ 个厉害的人和 $n - m$ 个不厉害的人；你要先在 $m$ 个厉害的人中选出若干个，厉害的人可以分别用左手和右手解决一个任务（也可以不解决）；不厉害的人只能用左手解决一个任务（也可以不解决），求最终解决 $k$ 个任务的方案数。不妨枚举最终 $k$ 个任务由 $x$ 个厉害的人双手解决、 $y$ 个不厉害的人左手解决、 $k - 2 x - y$ 个厉害的人单手解决，那么剩下没做任务的厉害的人既可以被选也可以不被选，单手做任务的厉害的人既可以左手做任务也可以右手做任务；于是总方案数就是
$\sum_{x=0}^{\lfloor k/2\rfloor}\binom {m}x\sum_{y=0}^{k-2x}\binom {n-m}y\binom{m-x}{k-2x-y}2^{m-x}=\sum_{x=0}^{\lfloor k/2\rfloor}2^{m-x}\binom {m}x\binom{n-x}{k-2x}$
预处理 $2$ 的光速幂次和 $0∼k0\sim k$ 的阶乘逆元，时间复杂度 $O(n+Tk2)O(\sqrt n+Tk^2)$ 。

硬推

考虑 $∑i=0m(mi)(ik)=∑i=0m(mk)(m−ki−k)=(mk)2m−k\sum_{i=0}^m\binom mi\binom {i}k=\sum_{i=0}^m\binom mk\binom{m-k}{i-k}=\binom mk2^{m-k}$ ，我们希望能将原式转化成这个样子。考虑 $(n−m+2ik)\binom{n-m+2i}k$ 可以看成是一个关于 $i$ 的 $k$ 次多项式 $∑j=0kajij\sum_{j=0}^ka_ji^j$ ，其中 $a_j$ 是把那个组合数展开后 $i^j$ 次项上关于 $n, m, k$ 的系数。一眼盯真，用换幂公式转为 $∑j=0kbj(ij)\sum_{j=0}^kb_j\binom ij$ 把通常幂转成下降幂变成组合数，带回原式有
$\sum_{i=0}^m\binom mi\sum_{j=0}^kb_j\binom{i}{j}=\sum_{j=0}^kb_j\binom{m}{j}2^{m-j}$
时间复杂度 $O(Tk^2)$ 。一开始的 $a_j$ 大概可以通过类似于乘法分配律的方式，枚举组合数的乘下降幂的时候贡献到哪个次数上，可以做到 $O(k^2)$ 。

T3

给定一个长度为 $n$ 序列的 $a$ ， $Q$ 次询问每次给定一个区间 $[l, r]$ ，求在把 $a [l : r]$ 的部分扣掉以后 $a$ 的最长严格上升子序列长度。

$1≤n,Q≤1051\le n,Q\le 10^5$ ，强制在线。

把 $[l, r]$ 扣掉，相当于我们只能在 $[1, l - 1]$ 找一个子序列，在 $[r + 1, n]$ 找一个子序列，且第一个子序列的末尾小于第二个子序列的开头，然后就能拼起来。设 $f (w)$ 表示在 $[1, l - 1]$ 中以 $w$ 结尾的最长上升子序列， $g (w)$ 表示在 $[r + 1, n]$ 中以 $w$ 开头的最长上升子序列，那么对于当前这个询问相当于求
$max_{i<l,r<j}[a_i<a_j](f(a_i)+g(a_j))$
不妨考察每个 $j$ ，相当于就是查 $max_{w<a_j}f(w)$ 即一个前缀最小值。

考虑分块。

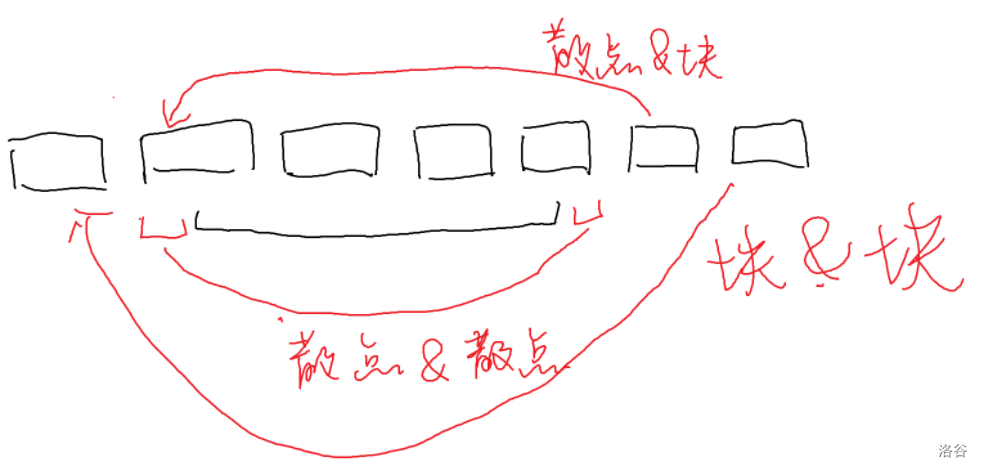
图中一个个黑色方框是分的块，黑色线段表示询问区间。

右边块对左边块的贡献：我们只需要枚举一边的块，在另一边一段前缀的块中查询即可。这里可以预处理的，设 $f (l, r)$ 表示第 $1∼l1\sim l$ 个块对第 $r$ 个块的贡献，从小到大枚举 $l$ ，设一个数组 $t ab$ ，将 $1∼l1\sim l$ 个块中的元素 $i$ 的答案 $f (i)$ 放在 $tab_{a_i}$ 上，然后做一个前缀 max，枚举第 $r$ 个块中的元素一个个放进数组中查询，预处理时间复杂度 $O(nn)O(n\sqrt n)$ 。
右边的块对左边散点的贡献：我们预处理出每个前缀的块建出的树状数组，然后查询树状数组即可，时间复杂度 $O(nlog⁡n)O(\sqrt n\log n)$ 。
右边的散点对左边块的贡献：与上面类似。
右边散点对左边散点的贡献：我们可以把散点拿出来，按照这个点 $a$ 的值从小到大排序，然后从前往后扫描，每有一个左边的散点就可以更新此时的 $f (w)$ 的值；每有一个右边的散点就可以直接查询。时间复杂度 $O(nlog⁡n)O(\sqrt n\log \sqrt n)$ 。

可以发现处理有关散点的贡献时总是带一个 log。考虑优化：我们直接令 $F (l, i)$ 表示 $[i, n]$ 中散点和块对前 $l$ 个块的总贡献，用类似块对块的方法做就可以 $O(nn)O(n\sqrt n)$ 预处理好；同理 $G (r, i)$ 表示 $[1, n]$ 中散点和块对后 $r$ 个块的总贡献；拼起来就是块与块、点与块、块与点三个贡献。

再考虑散点对散点时要对排序，可以考虑先把每个块排序，每次对两拨散点排序时直接抽出子序列然后归并。这样时间复杂度就是 $O(nn)O(n\sqrt n)$ 的了。

#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f; 
const ll linf = 1e18; 
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 1e5 + 5, maxm = 325;
int n, Q, tp, a[maxn], val[maxn], m;
int F[maxm][maxn], G[maxm][maxn], k, len;
// 左边块对右边散点  右边块对左边散点
int L[maxm], R[maxm], bel[maxn];
int f[maxn], g[maxn], f_mx[maxn], g_mx[maxn]; // 前缀答案 后缀答案
struct BIT {int b[maxn];void clear() { memset(b, 0, sizeof(b)); }void add(int x, int v) {for (; x <= m; x += lowbit(x))chkmax(b[x], v);} int ask(int x) {int res = 0;for (; x; x -= lowbit(x))chkmax(res, b[x]);return res;}
} tab; int tmp[maxn]; vector<pair<int, int> > arr[maxm];
bool MemoryED; int main() { // open(data);scanf("%d %d", &n, &tp), len = sqrt(n);for (int i = 1; i <= n; i ++)scanf("%d", &a[i]), val[i] = a[i];sort(val + 1, val + n + 1), m = unique(val + 1, val + n + 1) - val - 1;for (int i = 1; i <= n; i ++) {a[i] = lower_bound(val + 1, val + m + 1, a[i]) - val;// cerr << a[i] << " \n"[i == n];}for (int i = 1; i <= n; i ++)tab.add(a[i], f[i] = 1 + tab.ask(a[i] - 1)), f_mx[i] = max(f[i], f_mx[i - 1]);tab.clear();for (int i = n; i; i --)tab.add(m - a[i] + 1, g[i] = 1 + tab.ask(m - a[i])), g_mx[i] = max(g[i], g_mx[i + 1]);for (int _ = 1; _ <= n; _ += len) {L[++ k] = _, R[k] = min(_ + len - 1, n);for (int i = _; i <= n && i < _ + len; i ++) bel[i] = k, arr[k].emplace_back(a[i], i);sort(arr[k].begin(), arr[k].end());} for (int i = 1; i <= k; i ++) {for (int j = 1; j <= m; j ++) tmp[j] = 0;for (int j = 1; j <= R[i]; j ++)chkmax(tmp[a[j]], f[j]);for (int j = 1; j <= m; j ++)chkmax(tmp[j], tmp[j - 1]);for (int j = n; j > R[i]; j --)F[i][j] = max(F[i][j + 1], g[j] + tmp[a[j] - 1]);} for (int i = k; i; i --) {for (int j = 1; j <= m; j ++) tmp[j] = 0;for (int j = L[i]; j <= n; j ++)chkmax(tmp[a[j]], g[j]);for (int j = m; j; j --)chkmax(tmp[j], tmp[j + 1]);for (int j = 1; j < L[i]; j ++)G[i][j] = max(G[i][j - 1], f[j] + tmp[a[j] + 1]);} scanf("%d", &Q);for (int _ = 1, lstans = 0; _ <= Q; _ ++) {int l, r; scanf("%d %d", &l, &r);if (tp) l ^= lstans, r ^= lstans;if (l == 1 && r == n) { puts("0"), lstans = 0; continue; }if (l == 1) { printf("%d\n", lstans = g_mx[r + 1]); continue; }if (r == n) { printf("%d\n", lstans = f_mx[l - 1]); continue; }l --, r ++;int bl = bel[l], br = bel[r], ans = max(max(f_mx[l], g_mx[r]), max(F[bl - 1][r], G[br + 1][l]));// cerr << _ << ' ' << bl << ' ' << br << '\n';vector<pair<int, int> > tmp1, tmp2, tmp3;for (auto i : arr[bl]) if (i.second <= l) tmp1.emplace_back(i.first, i.second);for (auto i : arr[br]) if (i.second >= r) tmp2.emplace_back(i.first - 1, i.second);tmp3.resize(tmp1.size() + tmp2.size());merge(tmp1.begin(), tmp1.end(), tmp2.begin(), tmp2.end(), tmp3.begin());for (int now = 0; auto [val, pos] : tmp3) {if (pos <= l) chkmax(now, f[pos]);else chkmax(ans, now + g[pos]);} printf("%d\n", lstans = ans);}return 0;
}