当前位置：首页 > news >正文

斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记 | Lecture 9: Scaling laws 1

news 2025/11/17 8:09:26

- 前言
- 1. Overview
- 2. Part 1. Scaling laws, history and background
- - 2.1 Data scaling as empirical sample complexities
  - 2.2 Initial forays into understanding neural scaling with data
- 3. Part 2. Neural (LLM) scaling behaviors
- - 3.1 Data vs performance
  - 3.2 Other data scaling laws
  - 3.3 Recap: data scaling laws
  - 3.4 Hyper-parameters vs performance
  - - 3.4.1 Architecture
    - 3.4.2 Optimizer
    - 3.4.3 Depth/Width
    - 3.4.4 Batch size
    - 3.4.5 Learning rates
  - 3.5 Scaling behaviors can differ downstream
  - 3.6 Model-data joint scaling
  - 3.7 Chinchilla in depth – 3 methods
  - 3.8 Recent example for different (diffusion) models
- 4. Recap: scaling laws – surprising and useful!
- 结语
- 参考

前言

学习斯坦福的 CS336 课程，本篇文章记录课程第九讲：缩放定律（上），记录下个人学习笔记，仅供自己参考😄

website：https://stanford-cs336.github.io/spring2025

video：https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_

materials：https://github.com/stanford-cs336/spring2025-lectures

course material：https://stanford-cs336.github.io/spring2025-lectures/blob/lecture_09-Scaling_laws_basics.pdf

1. Overview

这次课程我们来简单谈谈 缩放定律（scaling laws），说到缩放定律的核心意义，首先，请大家设想这样一个场景：假设你有一位非常富有的朋友，他慷慨地借给你 10 万张 H100 显卡，使用期限一个月，而你需要在期限内打造出最优秀的开源语言模型

这个任务颇具挑战性，我们已经为你准备了一些攻克这个难题所需的工具，现在你可以组建自己的基础设施团队和系统专家小组，同时你还能搭建一套分布式训练框架，在接下来的任务中，你将需要整合出一个优质的预训练数据集，而你对模型架构这些知识已然了然于胸。可以说，你现在已经掌握了所有关键要素，这样我们就能开动机器，运行这个大模型了

在这里插入图片描述

在前几节课中，我们已经讨论过这个过程中可能需要做出的各种决策，比如：该选用什么架构，该设置哪些超参数，这些具体要怎么实现等等，某种程度上，前几节课给出的答案就是：直接沿用业界通用方案，直接参照 Llama 或其他成熟模型的做法就好。但某种程度上，这个答案太过保守，它无法推动技术边界的突破，如果你身处顶尖实验室，目标是打造最优秀的模型，就不能止步于复制他人的成果，必须勇于创新突破，那么，我们究竟该如何创新并率先获得这些优化方案呢？

这正是缩放定律的核心价值所在，我们的目标是建立简洁、可预测的语言模型行为规律，缩放定律的核心思想在于：通过将小型模型逐步扩展升级，以此推动工程实践的持续优化。传统深度学习那种令人头疼的做法就是盲目训练一大堆模型，通过反复调试超参数来勉强提升大模型性能，这种做法只会消耗海量的计算资源，实际操作中根本难以持续

因此，当前这种围绕模型扩展的新兴研究趋势令人振奋，如果你持续关注相关进展，就会意识到这才是正确方向，我们将先训练一批小型模型，从中积累经验教训，再将所得规律逆向推广至更大规模的模型，我们将从计算规模最小的模型入手，通过充分学习训练规律后，最终在构建大模型时实现一次性成功

2. Part 1. Scaling laws, history and background

首先我们从缩放定律的发展历程和背景讲起，需要特别说明的是，当前关于缩放定律的讨论绝非仅仅是在双对数坐标上拟合直线那么简单，接下来我们将采用循序渐进的方式展开讲解

2.1 Data scaling as empirical sample complexities

我们从统计机器学习的理论基础开始讲起，缩放定律究竟是什么？从本质上说，缩放定律揭示了这样一个规律：当我们增加数据量或调整模型规模时，模型性能会呈现出特定的变化趋势。

回顾机器学习基础理论时，如果你还记得 [Vapnik–Chervonenkis dimension] 和 [Rademacher complexity] 这些核心概念的话，这些理论本质上就是对缩放现象的数学诠释

$ϵ(h^)≤(min⁡h∈Hϵ(h))+21mlog⁡2kδ\epsilon(\hat{h})\leq\big(\min\nolimits_{h\in H}\epsilon(h)\big)+2\sqrt{ \tfrac{1}{m}\log\tfrac{2k}{\delta}}$

我们得到了关于有限假设集（包含 k 个假设）中学习过程超额风险的泛化误差上界，如上式所示，我们发现这个上界应该按照 $1mlog⁡2kδ\sqrt{ \tfrac{1}{m}\log\tfrac{2k}{\delta}}$ 的比例变化，这本质就是缩放定律的理论表现形式，我们通过这个规律可以预测：随着样本量 $m$ 的增加，模型误差将以怎样的速率衰减。而在生成式建模领域，当我们使用高度灵活的非参数模型时，情况会变得更为复杂

在这里插入图片描述

此时可能会出现一些超出常规的缩放定律，我们可能会转而拟合某种平滑的概率密度函数，因此在这种情况下，我们预测密度估计的 L2 误差上界将遵循 $n−β2β+1n^{-\frac{\beta}{2\beta+1}}$ 的多项式规律，这就是学界常说的 非参数收敛速率

理论家长期致力于研究样本量与误差之间的内在关联，这是机器学习理论研究中一个经典的核心命题，但这仅仅是理论上界，而非实际达到的损失值，从本质上看，缩放定律实现了从理论推导向实证研究的跨越，它不再拘泥于 “数据规模与模型性能应该如何关联” 的理论推演，而是转向实证层面坦言 “我们的理论边界存在局限，但或许可以通过实际数据拟合出规律”

这里有个有趣的冷知识，或者说存在争议的冷知识，那就是哪篇论文最早提出了缩放定律呢？真正开创性的缩放定律论文当属 1993 年贝尔实验室发表在 NeurIPS 上的那篇

在这里插入图片描述

这些作者的名字你可能并不陌生，他们堪称理论派代表，其中不乏在机器学习理论领域做出开创性贡献的学者，VC 理论的 Vapnik，开发支持向量机的 Corinna Cortes 等重量级人物，这篇论文在许多方面都展现出惊人的前瞻性，其观点至今仍然正确。论文指出：在大规模数据库上训练分类器的计算成本极高，因此我们需要在实际训练前就能有效评估模型的潜力，为此，我们提出了一种创新的预测方法，无需完整模型训练，即可预判其最终性能表现

这听起来与缩放定律的理念高度吻合，但其函数形式本质上可表述为：模型的测试误差等于某个不可约误差项加上一个多项式衰减项：

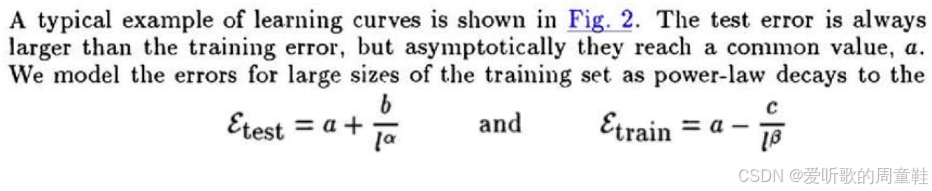
在这里插入图片描述

这不正是现代缩放定律的典型表达形式吗？更令人惊叹的是，他们通过训练多个小型模型拟合曲线后，发现这种方法竟能准确预测模型在更大规模下的表现

由此可见，缩放定律的雏形早在贝尔实验室时期就已出现端倪，这似乎印证了许多重大发现都经历过类似的 “前世今生”

2.2 Initial forays into understanding neural scaling with data

当然，除了缩放定律本身，还有其他研究者对规模化的相关理念进行了深入思考，这种关于规模效应的现代思维方式同样值得关注。在缩放定律的发展历程中，还有一篇常被提及来自 Benco 和 Brill 的论文，他们研究的问题是：某类自然语言处理系统的性能如何随着数据量的增加而变化？

在这里插入图片描述

上面这些数据呈现出典型的现代缩放定律特征：横轴采用对数坐标，纵轴表示性能指标，他们实质上是在论证：仅仅通过扩大数据规模，我们就能获得极其显著的性能提升，这种规律具有高度可预测性，或许我们需要取舍：是将资源投入算法研发，还是直接用于扩充数据规模，这听起来不正和当前预训练领域的主流思路如出一辙吗？

最后，无论是过去还是现在，人们始终在思考一个问题：这种规律真的具有可预测性吗？怎样的函数形式才是正确的表达呢？早在 2012 年，研究者们就已深入探讨这种规律是否真的可预测性

比如幂次为 3 或 4 的幂律是否真能准确预测模型的行为表现，需要特别说明的是，上述所有讨论都是围绕模型能力（纵轴）随训练数据量（横轴）变化的函数关系展开的，这正是学界长期研究的核心关系，在所有这类场景中，我们可称之为数据规模化的基本规律

若论神经网络缩放定律的开山之作，当属 Hestness 等人在 2017 年发表的那篇里程碑式论文，他们的研究证明：在机器翻译、语音识别以及部分视觉任务中，错误率遵循幂律下降规律，他们绘制了一张极具参考价值的图表：

它清晰地揭示了模型性能演变存在三个特征鲜明的区间；最初阶段，模型仅能进行随机猜测，随后进入可预测的缩放区间，这正是幂律主导的区域，最终会进入渐近区间，此时模型性能逐渐逼近该模型类别固有的不可约误差极限。需要特别指出的是，近年来学术界频繁讨论的新型涌现现象，比如所谓的 “能力涌现” 现象，或是算力扩展带来的新特性以及系统架构的关键作用

在这里插入图片描述

但若仔细研读过 Hestness 团队 2017 年的论文就会发现这些现象其实早有预见，该研究团队明确指出，实际上，当模型处于随机性能阶段时，基于缩放定律进行预测极其困难，因为系统随时可能突破随机性能区间，他们在研究中明确探讨了计算极限问题，事实上，能否实现缩放的关键在于—计算资源的规模化能力才是真正的决定性因素，最终他们甚至提出：或许我们应该采用量化等方法，既然缩放定律具有可预测性，就意味着我们可以通过牺牲计算效率来换取模型精度的提升

这些极具前瞻性的观点，其实早在早期的缩放定律论文中就已初现端倪，当研究者们看到那些呈现规律性变化的曲线图时，他们直观地意识到：只要资源投入可预测，模型能力的提升就同样可预测。这从某种意义上揭示了缩放定律的核心逻辑，虽非完整的发展历程，但正是这些关键认知奠定了缩放定律的理论根基

3. Part 2. Neural (LLM) scaling behaviors

现在我们要探讨大语言模型的缩放特性，接下来我们将重点梳理几组关键实验数据，我们将重点解析数据规模缩放的实证案例，通过这些具体示例向大家展示这种缩放定律的存在其实是水到渠成的必然现象，接着我们会讨论模型规模的问题，这完全是另一个维度的考量

缩放定律已经得到了相当充分的验证，这些规律在众多变量中反复出现，呈现出惊人的普适性：

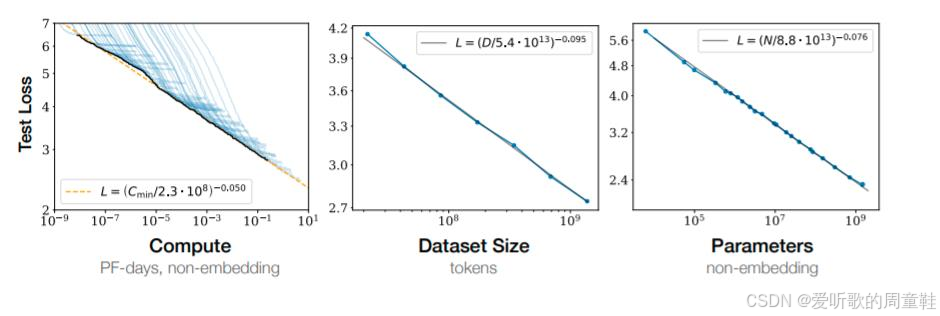
在这里插入图片描述

在横坐标上，大家会看到计算资源的规模变化，这些数据均引自 [Kaplan+ 2020] 的缩放定律论文，本课程将频繁引用该研究，这里的横轴采用对数计算（log compute）表示，纵轴则对应对数测试损失（log test loss），其右侧图表则展示了数据集规模呈现的类似的缩放定律，最后显示的是参数规模的变化

在讨论缩放定律时需要特别需要注意一个细节：当我们对数据集规模或模型参数进行扩展时，总是假设另一个变量（比如扩展数据集时对应的模型规模）必须足够大，大到足以避免被当前数据集规模所饱和，因为很显然，当数据量远超参数规模时，模型性能最终会达到饱和状态，因此在所有实验中，我们都在设法避开这种性能饱和的情况

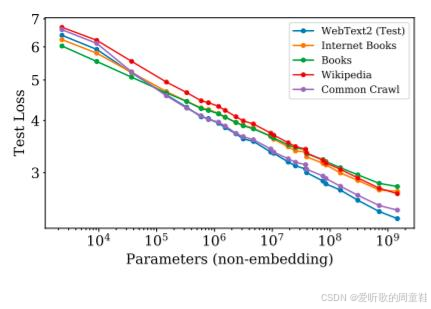
在这里插入图片描述

这些规律在相对非标准化的实验环境下同样成立，这些规律同样适用于下游任务，这些规律在分布外数据上依然适用，Kaplan 论文中的结果正印证了这一点，从某些角度来看，幂律关系的出现频率远超我们最初预期，特别是在处理离群值或其他变量时尤为明显

3.1 Data vs performance

首先我们来谈谈数据缩放定律，这是最直观的部分，因为这背后的理论框架已经相当清晰。准确地说，当我们提到 “数据缩放” 时，指的是一个简单的数学关系式：将数据集大小（记为 n）映射到我们的超额误差上，超额误差指的是超出不可约误差范围的那部分误差

还记得我们在 Hestness 研究中提到的那个图表吗，我们预期看到的应该是单调的、类似逻辑函数的曲线，我们真正关注的主要是幂律区域到不可约区域的这段关系，当然，研究小数据区域（即脱离随机猜测阶段）的变化规律也很有意思，但其规律性要难分析得多，相比之下，右侧尾部的规律更为明晰。希望接下来能让大家相信：这种呈现幂律扩展的现象，本质上是非常自然且符合预期的

OK，我们首先观察到的实证现象是：当我们以数据集规模为横轴、测试损失为纵轴，在双对数坐标系中，模型性能呈现完美的线性关系

这种现象可称为 无尺度（scale-free）特性，亦可称作 幂律（power law）关系，这些表述更偏向物理学领域的术语体系，这一规律已被众多研究者反复验证，具体案例可参考 Kaplan 等人的研究文献

正如前文所述，我们通常预期误差会呈现单调变化趋势，随着训练数据量的增加，误差理应逐步降低，这个结论相当直观，真正值得探讨的是这种缩放关系所遵循的具体数学规律。当我们说这是幂律关系时，指的是在双对数坐标系下呈现线性特征，那么这种特征究竟意味着什么？当某个关系在双对数坐标系下呈现线性时，就意味着横轴与纵轴变量之间存在多项式关联，而纵轴变量呈现自然多项式衰减

下面我们将通过两个典型案例来具体解析，这两个案例最终都会呈现出相当自然的多项式衰减规律，让我们从最简单的示例开始讲起，这个示例甚至不需要机器学习基础，用统计学入门知识就能解释

假设我们需要估算一个数据集的均值，均值估算本质上是一个参数估计问题，我们可以探讨其中的缩放定律是：均值估计的误差如何随数据变化呢？我们可以用公式来表示这个关系，假设输入数据服从高斯分布即 $x1⋯xn∼N(μ,σ2)x_{1} \cdots x_{n} \sim N \left( \mu, \sigma^{2} \right)$ ，当前任务为估计该分布的均值即 $μ^=∑ixin\widehat{ \mu}= \frac{ \sum_{i}x_{i}}{n}$

根据标准论证过程，这个平均值同样服从高斯分布，其标准差将缩小为原值的 $1n\frac{1}{n}$ 倍，这样我们的估计误差就是 $σ2n\frac{\sigma ^2}{n}$ ，也就是说 $E[(μ^−μ)2]=σ2nE \left[ \left( \widehat{ \mu}- \mu \right)^{2} \right]= \frac{ \sigma^{2}}{n}$ ，这正是我们估计量的期望平方误差

从表达式来看，这个误差与 $n$ 呈多项式关系，为了直观理解，我们对等式两边取对数，得到 $log⁡(Error)=−log⁡n+2log⁡σ\log \left( Error \right)=- \log n+2 \log \sigma$ ，左边是误差的对数，右边是样本量的对数加上两倍标准差对数，这正是我们预期的典型关系式，若为均值估计拟合缩放定律，我们预期斜率应为 1

掌握了这个新认知后，你可能会说：OK，接下来我要系统性地研究不同估计目标的收敛速率，这就能揭示数据规模扩展时的预期规律，于是你可能会恍然大悟，原来预期收敛速率是 $1n\frac{1}{n}$ 啊，在不可知学习场景中，你可能会预测预期速率为 $1n\frac{1}{\sqrt{n}}$ ，诸如此类的规律会逐步显现，因此在双对数坐标图中，我们预期会看到斜率为 1 或 0.5 这样的典型数值

当我们实证分析这些论文时，实际观测到的规律是怎样的呢？具体数据如下：

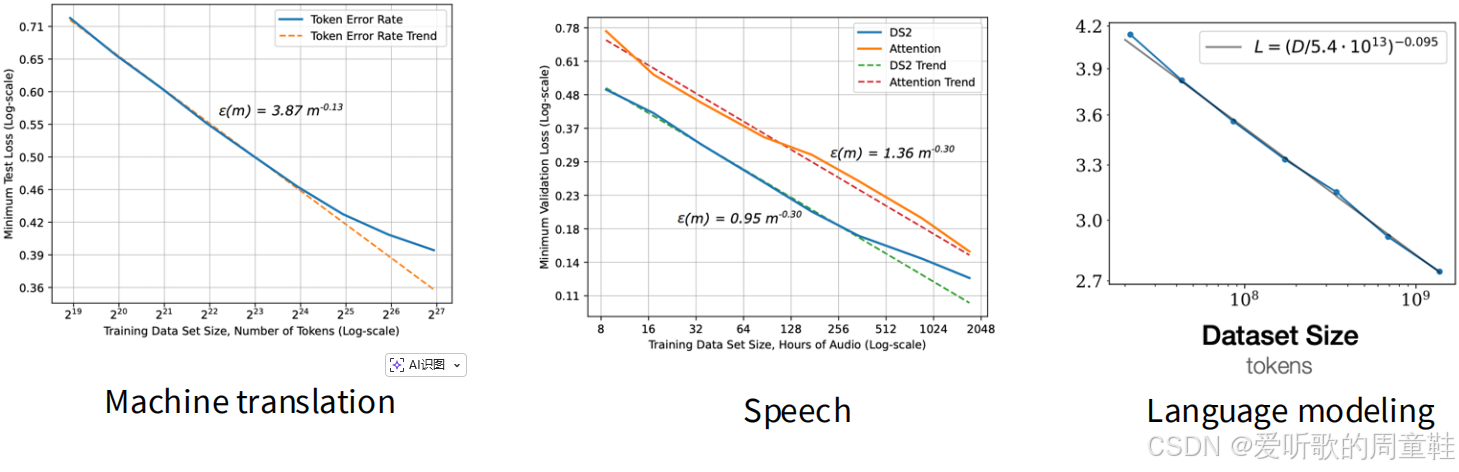
在这里插入图片描述

在 Hestness 的研究中，机器翻译任务的指数为 -0.13，语音识别领域观测到 -0.3 的指数，而语言建模任务则呈现出 -0.095 的指数特征，这些指数衰减速度（-0.13、-0.3、-0.095）都显著慢于传统简单函数拟合中预期的 $1n\frac{1}{n}$ 或 $1n\frac{1}{\sqrt{n}}$ 收敛速率。那么，为何会出现这种现象呢？众所周知，神经网络的功能远不止于均值估计，它甚至不只是在做线性回归拟合，神经网络能够拟合任意复杂的函数关系，让我们通过具体案例来展开说明，逐步剖析这个原理

我们的输入是 $x1…xnx_1 \dots x_n$ ，现有 $n$ 个样本点，我们将把它们均匀分布在二维单位正方形区域内，现在需要估计某个（非随机的）任意回归函数 $y = f (x)$ ，假设函数 $f$ 具有平滑等性质，一种非常简单的非参数回归方法是：先将空间划分成若干区域，再对各区域内的数据进行独立估计

通俗来说，如果我们划分出 $n\sqrt{n}$ 个方格，每个方格将分配到 $n\sqrt{n}$ 个样本，此时误差项就是 $1n\frac{1}{\sqrt{n}}$ ，将这个逻辑推广到更高维度时，我们会发现：在 D 维空间中，误差项将遵循 $Error = n^{-1/d}$ 的关系，那么整体的缩放规律就呈现为 $n^{-1/d}$ 的衰减趋势，如果绘制对数坐标图，我们预期会得到斜率为 $−1d-\frac{1}{d}$ 的直线

那么，我们为什么要来推导这个例子呢？之所以详细讲解这个例子，是因为 当我们面对灵活的函数类别（即学界所称的非参数化函数类别）时，维度依赖效应会导致缩放定律的斜率变化显著趋缓。从某种意义上说，这个斜率几乎精确地揭示了任务本身的内在维度特性或学习难度

学界对此已有更严谨的理论论证，近期多篇理论与实证研究论文 [Bahri+ 2021] 指出，这些非标准学习速率的出现，实际上与数据的内在维度密切相关：

例如，从上面这些预测曲线来看（虚线部分与紫色圆点标记），两者趋势确实存在一定程度的吻合，不过我们不宜过度解读这种关联性，因为内在维度的估计本身就是个极其困难的课题，其难度不亚于对数据整体进行建模

3.2 Other data scaling laws

数据缩放定律的实际应用远不止于此，它能实现诸多令人惊艳的功能，工程师们会基于数据缩放定律做出各类技术决策，这已成为行业内的标准实践。举例来说，我们不仅要关注数据集规模，更要思考数据集的构成是如何影响模型性能的，Kaplan 等人的研究给出了精妙图示：

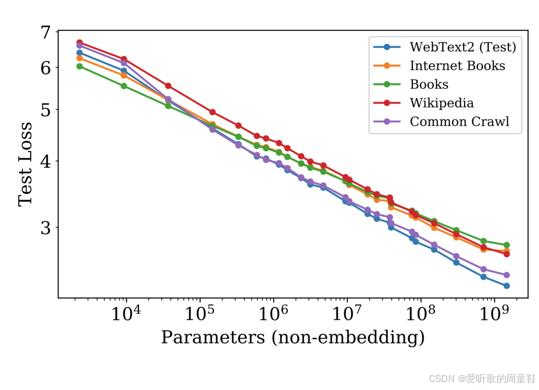
在这里插入图片描述

当测试集发生变化时，数据构成仅影响性能曲线的截距，而不会改变其斜率，这意味着要选择优质数据集，未必需要大规模训练模型，完全可以在缩小规模后，用更小的模型开展数据筛选实验。当我们混合不同数据时，性能曲线的预期形态往往呈现出特定规律，借助回归分析等技术手段，我们完全可以通过缩放定律来推演出最优的数据混合比例

在这里插入图片描述

目前已有数篇论文 [Hashimoto+ 2021] 探讨这一课题，但正如所有数据选择研究面临的困境，这些方法在实际操作中往往难以稳定复现，这个领域还存在着诸多值得探索的迷人问题

当前业界热议的一个焦点是：互联网上的可用数据是否即将耗尽？当深入探讨这个问题时，另一个关键议题随之浮现：我们能否仅依靠现有数据进行持续训练？这种做法的收益递减特性究竟如何呈现？当前学界正开展一项引入注目的研究：将缩放定律应用于多轮次训练。研究表明：数据存在 “有效样本量” 现象，当训练轮次超过四轮后，随着数据重复使用次数的增加，模型性能提升将呈现急剧衰减的趋势

在这里插入图片描述

通过调整传统的缩放定律，我们可以推导出一个新版本：随着数据重复次数的增加，有效数据量和唯一 token 数会呈现递减关系，即：

$D′=UD+UDRD∗(1−e−RDRD∗)D^{\prime}=U_{D}+U_{D}R_{D}^{*}(1-e^{\frac{-R_{D}}{R_{D}^{*}}})$

其中：

$D′D^{\prime}$ 代表有效数据量
$U_d$ 代表唯一 token 数
$R_{D}^{*}$ 为常量
$R_D$ 代表重复次数

这两种思路在大规模数据场景下的数据选择问题上能产生极具启发性的结合，假设我们要训练一个数万亿 token 规模的模型，那么，究竟哪种方案更具优势呢？在高质量数据（如维基百科和某些未公开书籍）重复使用十次与引入全新数据之间，究竟哪种策略更优呢？

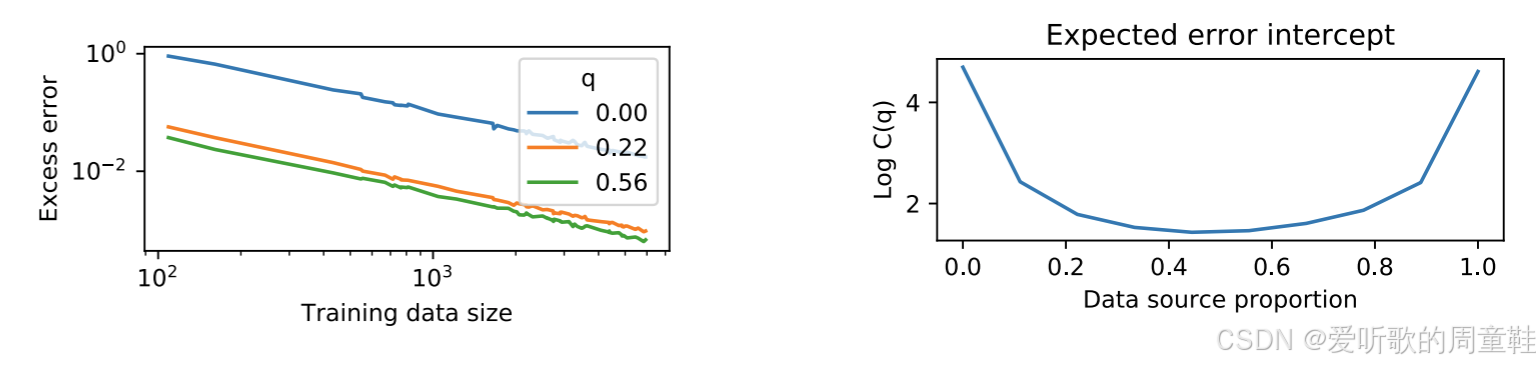
数据优化策略实际上存在多个可调节维度，既可以通过重复使用现有数据，也可以通过引入新数据来调整训练集的构成。卡内基梅隆大学的研究团队近期发表了一项关于数据缩放的有趣研究：

在这里插入图片描述

该成果重点探讨了在数据重复使用与选择低质量数据之间的取舍关系，这个发现颇具新意，只要假设存在预测性的幂律关系，且该关系在每个混合数据集中都成立，就能通过拟合这些缩放定律的外推曲线进而预估大规模数据集的预期效果

3.3 Recap: data scaling laws

以上就是我们的出发点—数据缩放定律，通过实证与理论的双重验证，相信大家已经能够理解数据量与误差之间呈现双对数线性关系，这其实是符合内在规律的必然现象。这种关联性在不同领域、各类模型中都展现出惊人的普适性，我们完全可以构建一套清晰完备的理论框架，来透彻理解这一现象的本质，掌握了这个原理后，就能将其运用于诸多场景，比如筛选最优数据组合，或是实现其他各类优化目标

3.4 Hyper-parameters vs performance

接下来我们要探讨的是一系列更具实践意义的工程问题，假设你现在负责构建并部署一个超大规模语言模型，当前这个领域涌现了许多引人入胜的创新思路，你可以选择训练最先进的状态空间模型，也可以选择训练 Transformer 架构，可以采用 Adam 优化器或者选用 SGD，研究者们在不断开发出各种新技巧

那么哪些方法值得扩展规模，哪些不值得呢？我们可以选择延长模型训练时间，或者扩大模型规模，在固定计算量（FLOP）的前提下，可以在二者之间进行取舍，当然我们也可以选择收集更多数据，或是增加 GPU 配置，有多种不同的策略可供选择。缩放定律为我们提供了一套简明的方法论，可以系统地解答这些问题，下面我们将解析经典地 Kaplan 缩放定律论文，主要包括以下内容：

Architecture
Optimizer
Aspect ratio / depth
Batch size

虽然其中部分内容已有时日，但就其研究深度而言，这篇论文在统一框架下展开的全面分析至今难有匹敌

3.4.1 Architecture

从架构选择的角度来看，我们首先需要探讨的是 Transformer 和 LSTM 究竟哪种更胜一筹，最直接的方法或许是尝试将 LSTM 扩展到 GPT-3 级别的规模，这样就能验证其实际效果究竟如何。而缩放定律的验证方式则更为简洁，具体操作是：在多个不同计算量级上训练一批 LSTM 和 Transformer 模型，然后观察它们在规模扩展过程中的表现差异

从上图来看，其中的规律已经相当明显，无论 LSTM 堆叠多少层，Transformer 与 LSTM 之间始终存在显著差异，这种性能差异体现为恒定的倍数关系。请注意，图中采用的是对数坐标，这意味着虽然具体数值尚不明确，但可以理解为 LSTM 的效率大约比 Transformer 低了 15 倍左右

在上面这张图表的所有区间内，LSTM 的计算效率始终比 Transformer 低约 15 倍，从这张图表来看，使用 LSTM 确实会带来恒定的计算效率损失，但更宏观的视角来看，其实存在着更多样的架构可能性

哪些架构真正优秀且值得投入呢？谷歌的 Tay 及其团队开展了这类规模扩展研究，他们选取了上图展示的多种架构，并对其进行了系统性扩展。横轴代表计算量，红线代表不同架构的表现，绿线则是 Transformer 基准模型的表现，他们提出的核心问题是：这些替代架构能否达到甚至超越 Transformer 的扩展能力？

最终结果如何呢？实际上，唯一能稳定超越 Transformer 的架构是门控线性单元（GLU）和专家混合（MoE）模型，这正是当前研究领域最前沿的探索方向，这本质上是用缩放定律的视角来解答同一个核心问题：我们究竟是如何得出应该采用 Switch Transformers 和 GLU 架构，而非 Performer 等方案这一结论的，缩放定律为此提供了明确的实证依据

3.4.2 Optimizer

优化器的选择也遵循类似的规律，这个观点源自 Hestness 的研究：

他们对比了 SGD 和 Adam 优化器，研究发现与先前结论高度一致：在计算资源（具体表现为数据集规模）相同的情况下，Adam 和 SGD 之间存在恒定的差距，这种差距最终会转化为两者在计算效率上的差异，图中 RHN 特指 Recurrent Highway Networks 网络，此处细节可暂不深究，重点在于理解这种分析方法的核心思路

3.4.3 Depth/Width

最初我们也提出过类似问题：深度与宽度之间究竟该保持怎样的比例关系？这正是我们讨论过的超参数议题之一，而我们在 Kaplan 的研究中，也看到了类似的分析框架，只不过是以缩放定律的形式呈现

这个发现确实耐人寻味，因为我们可能原本预期，随着网络层数加深，模型性能会出现显著提升，不同层数之间会呈现明显的性能差异，但实际数据表明：这里存在着相当大的浮动空间，单层网络的表现确实很差，但其他层数的选择却保持着惊人的稳定性。我们在架构讲座中曾经说过：宽度与深度的比例（aspect ratio）大致在 4~16 这个范围，是个比较自然的数值，只要落在这个范围内，模型表现都能接近最优，这项缩放定律分析也印证了这一点

需要特别指出一个容易被人忽视的关键细节：并非所有参数都具有同等重要性，这一点时常让研究者们栽跟头，在进行参数规模分析时，我们通常需要特别关注这一点，但若将嵌入参数也计入模型总参数量，你会发现缩放定律会发生显著变化

在这里插入图片描述

此时你会观察到一种略显异常的曲线形态—在某个区域会出现轻微的下弯现象，而如果仅考虑非嵌入参数，就能得到我们之前展示的那种更为规整的结果，由此可见，嵌入层参数确实呈现出不同的扩展特性，当把这些参数纳入考量时，它们并不像非嵌入参数那样呈现对数线性缩放定律

近期关于混合专家模型（Mixture of Experts）规模扩展的研究也提出了类似观点：并非所有参数都具有同等价值，这些研究正在探讨一个核心问题—当模型使用稀疏激活参数时，“参数” 这一概念的实际意义究竟是什么。这类论文本质上试图推导出诸如等效稠密参数量等指标，目的是为了对 MoE 种的参数数量进行标准化比较

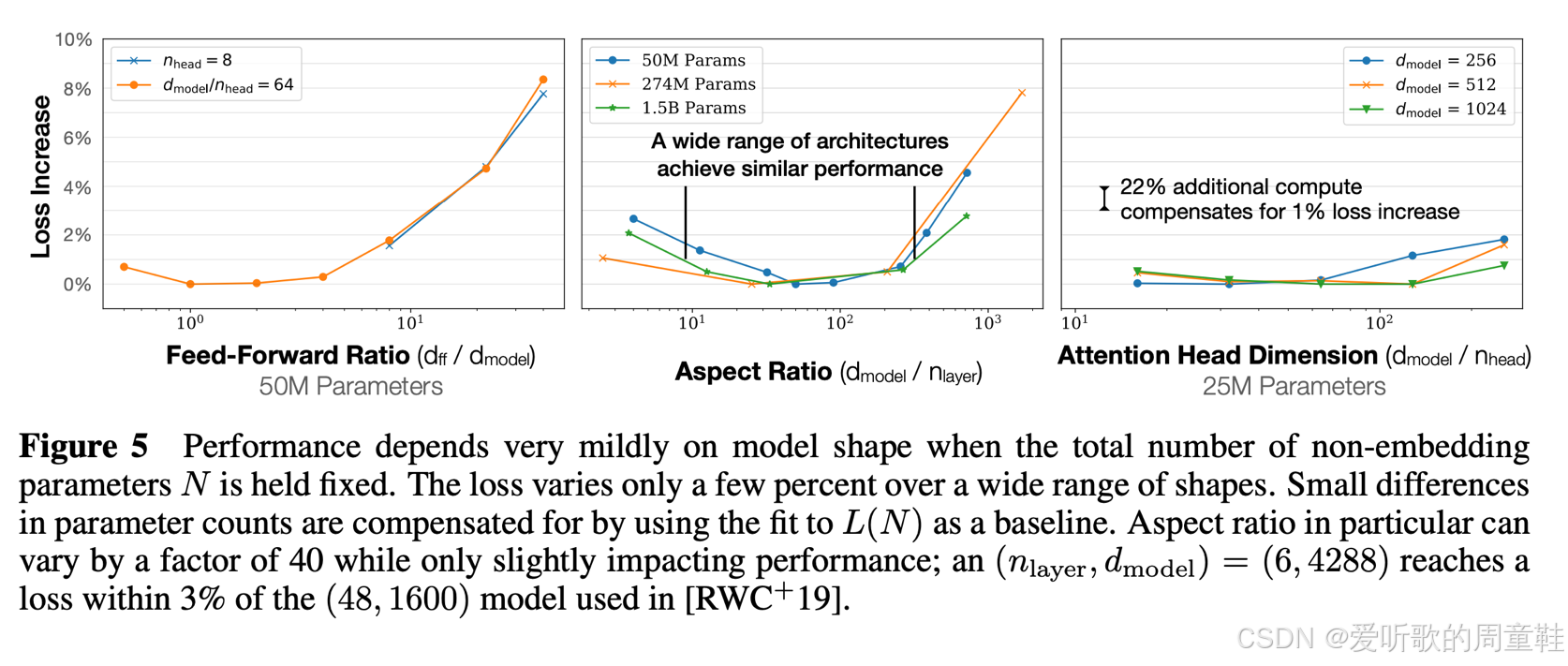
在这里插入图片描述

之前在超参数选择部分我们已经展示过上面这张图表了，不过现在希望大家能理解完整的背景脉络，而不仅仅是当初那个单纯的超参数选择问题。我们知道在很多情况下，规模扩展曲线的斜率通常保持高度相似，它们彼此不相交，而且这些曲线之间存在恒定的偏移量，只要这种情况成立，我们就可以在特定计算量或特定超参数组合下截取一个剖面，仔细分析超参数间的取舍关系，基于这个前提，就能放心地进行规模扩展

翻阅 Kaplan 地论文时，你会发现他们正是采用了这类分析方法，特别是上图的中间那张宽深比分析图，绝对值得仔细研究，他们并非简单地进行模型缩放，而是真正从不同维度切入分析，他们选取了 5000 万、2.7 亿和 15 亿参数规模的模型，专门研究宽深比对损失函数的影响，研究发现，不仅扩展斜率保持稳定，整个曲线的形态特征也呈现出高度相似性。这意味着在 10~100 的宽深比范围内，任意取值都能在不同规模下保持良好性能，这个问题值得我们深入思考

初学深度学习模型训练时，人们往往只关注超参数调优，但随着经验积累，你会意识到必须结合模型规模来调整这些参数，这种思维模式的转变至关重要。传统的小规模模型调优思路与遵循缩放定律的研究方法存在本质区别，前者习惯在有限算力下微调参数，后者则要求我们始终以规模扩展的视角来审视每个超参数的选择

同样的方法论也适用于前馈网络比率和注意力头维度的调整，都需要在模型扩展的框架下进行系统性优化，而非孤立地进行局部调优，你正在系统性地调整模型的各个规模参数，通过实验观察这些变化是否会导致最优解区域发生显著偏移

3.4.4 Batch size

后续阶段我们将通过实际案例向大家展示业界如何实现模型规模扩展的，我们会发现，当进行模型扩展时，批量大小和学习率这两个参数需要特别谨慎地处理。因此在进行规模扩展时，你需要考虑不同规模模型可能需要采用不同的最优学习率，这种情况下，最优批量大小往往也需要相应调整，因为这两个参数通常是相互关联的

因此我们必须深入思考：如何正确调整 batch size 以及 batch size 与模型规模、学习率之间的动态关系，接下来我们将重点讲解这些内容。在之前的系统课程中大家应该记得，batch size 超过某个临界值后会产生收益递减效应

在这里插入图片描述

在达到某个临界点之前，当 batch size 小于噪声尺度时，即图示左侧区域，增大 batch size 几乎等同于增加梯度更新次数，这大致意味着如果将 batch size 翻倍，效果相当于进行两次梯度更新，这种状态是最理想的优化区间，因为此时既能发挥系统并行处理批量数据的优势，又能获得相当于两次梯度更新的优化效率

但超过某个临界点，扩展效率就会急剧下降，当 batch size 达到噪声尺度时，新增的样本数据已无法有效降低系统噪声，可以说，此时优化曲面的偏置项曲率开始主导整个训练过程。其中，临界 batch size 这个概念堪称绝佳的分析工具，临界 batch size 可视为一个关键转折点，超过该值后，模型性能将从线程增长阶段进入收益急剧递减阶段

OpenAI 关于临界 batch size 的研究论文对此进行了深入的理论分析，但同样可以通过实证研究来验证这一现象，这种现象同样属于缩放定律的研究范畴，我们可以精确测算出模型性能增速开始放缓的临界点，通过实证研究可以测算出临界 batch size 的最优平衡点，同时还能训练出规模更大、性能更优的模型

这里有个非常有趣的现象：当你不断优化损失函数，也就是图中向左移动曲线使损失值越来越低，临界 batch size 实际上会逐渐变小，因此损失目标越小，可采用的总体 batch size 反而越大。这种现象带来的直接应用案例体现在 Llama 3 训练报告中，你会观察到训练团队在特定阶段后逐步扩大 batch size，甚至采用动态调整策略，随着损失目标的优化，batch size 反而能够相应增大

那随着计算资源和模型规模同步增长，我们该如何确定最佳策略呢？我们可以再次通过扩展性分析来寻找答案，这个观点源自 Kaplan 的研究

在这里插入图片描述

随着计算资源的增加，你可以尝试推算出最优 batch size 应该是多少呢？我们发现，随着计算量的增加，系统实际上能够实现相当程度的并行处理能力，在不超过当前计算阈值的情况下，在不断扩大 batch size 的同时总训练步数可以保持不变，而如果固定 batch size，训练步数自然会持续增加，这对数据并行处理来说无疑是个好消息

以上就是关于 batch size 的内容，关于临界 batch size 这个概念，虽然它确实有些复杂难懂，但需要记住当达到临界 batch size 时，就会出现收益递减的拐点；此外，临界 batch size 往往遵循可预测的缩放定律，通常与目标损失函数相关，基于此，我们就能在系统效率与优化进度之间找到最佳平衡点

3.4.5 Learning rates

正如前文所述，另一个关键因素在于 batch size 与学习率的协同关系，二者之间存在着紧密的关联性，在接下来的缩放定律讲座中，我们将更系统地深入讲解 $μP\mu \text{P}$ （最大更新参数化）理论

你可以选择以下两种方案之一：

在这里插入图片描述

我们先来看左侧这种标注为 “Standard Practice” 的图表，当你训练一个 Transformer 模型时，实际上看到的效果就会类似于左侧这张 “Standard Practice” 图表所示的情况，最佳学习率会出现在不同的训练阶段，随着模型规模的扩大，当你不断增加模型参数，使 MLP 的宽度持续增加时，最佳学习率会变得相当小，随着模型规模不断缩小，损失值自然会上升，因为模型的表达能力随之减弱，但与此同时，最佳学习率反而会逐渐增大

业界通常存在一个经验法则，最佳学习率的缩放比例应该与模型宽度成反比，即遵循 $1/ w i d t h$ 的规律，更资深的从业者通常会进行实际拟合，具体做法是：先通过这些曲线找到最小值点，然后针对最佳学习率拟合出相应的缩放规律。由此可见，学习率呈现可预测的衰减趋势，或许我们可以据此拟合出相应的缩放定律，关于这一点，我们会在接下来的系列讲座中进一步展开讨论

另一种做法已开始被广泛采用且极具思考价值，那就是对模型进行重参数化，具体而言，可以采取诸如根据网络宽度调整初始化范围，或基于不同层级的宽度差异来缩放对应学习率等操作。我们可以根据模型的宽度调整初始化的方差，同时在模型前向传播过程中对不同层的输出进行乘积缩放，通过这种与模型宽度相关的参数化方法最终得到的模型架构能够保持更稳定的学习率

按照原始论文的结论，这种稳定性在不同规模下可以达到精确维持，这样只需一次性调整学习率参数后续就无需再做任何改动，最优参数可以直接迁移应用，实际上，你只需在最小规模模型上调试一次参数，这些参数就能直接适用于最大规模的模型，这就是所谓的 $μP\mu \text{P}$ 参数化方法，后续还衍生了其他变体方法，例如 Meta 公司在发布 Llama 4 时声称发明了一种名为 “MetaP” 的技术。目前许多实验室都在关注这个研究方向，因为如果必须依赖预测最优学习率，那就得进行各种复杂的缩放定律拟合，虽然传统方法可能很不稳定，但若能对模型进行重新参数化或许就完全不需要再做任何参数调整了，当然，这比实际情况要乐观得多

3.5 Scaling behaviors can differ downstream

需要特别提醒的是，这些定律在分析对数损失时表现良好，因此我们采用下一个 token 预测的交叉熵进行训练。当缩放定律的目标函数是这些交叉熵时，其预测效果会表现得非常理想，但若试图直接基于下游任务或基准测试进行规模扩展，其表现规律性就会显著降低

在这里插入图片描述

上面左侧图表展示的是 Yi Tay 的论文成果，该研究对比了多种超参数配置与模型架构，如图所示，模型参数量（此处作为计算量的替代指标）与负对数困惑度呈现出完美的线性相关性，这表明无论模型深度、宽度或超参数的具体设置如何变化，真正起决定性作用的只有总计算量投入

这个结论既简洁又优美，但当你实际运用这些模型时，这要追溯到 2023 年的研究，当时研究者们还在使用 SuperGLUE 准确率这类指标，那此时这些模型的实际应用表现究竟如何呢？从图中我们可以看到已不再是那种完美的线性关系了，现在我们观察到的是另一番景象：某些模型表现远超同类，特定架构的优势也愈发凸显，因此，这种精确的缩放定律可能并不符合预期

类似的情况，我们已经在不同领域多次见证。纵观状态空间模型的相关文献，这正是我们反复观察到的现象，在状态空间模型中，我们确实能观察到如左图所示的优美而可预测的缩放定律，但通常仅适用于特定能力维度，比如在上下文学习或问答任务中，已有研究表明这类模型的表现可能稍逊一筹

因此必须注意，这种困惑度的扩展规律与下游任务的扩展表现不可混为一谈，在进行此类分析时，务必保持审慎态度

3.6 Model-data joint scaling

当我们面临超参数选择、架构设计等大量工程决策时，其实完全可以在模型训练开始前就完成大部分决策工作。我们完全可以在多个数量级的计算规模上，先对这些模型进行小规模训练验证，而后通过规模扩展就能预测更大模型的行为表现

基于缩放定律的设计流程其实非常简单，先训练几个小型模型，这些模型的算力需求应当跨越几个数量级，通过实验数据建立某种缩放定律，从已训练的模型中可以观察到性能指标与规模之间呈现出明显的对数线性关系，根据这个预测规律就能确定最优的超参数配置

实际上在多数情况下，这些缩放定律的变化幅度通常不会太大，其对数坐标下的斜率通常保持一致，由此得出的推论是：仅需训练几个小型模型，这些小型模型的实验结果就能出乎意料地良好迁移到大型模型上，不过学习率等关键参数往往属于例外情况，这就是进行超参数选择和架构选择的基本方法

现在我们要讨论缩放定律的一个极其重要的应用，这个应用对我们如何选择模型规模、如何考量模型的数据效率等问题产生了深远影响。回想早期人们刚开始扩展这些模型规模时，有个根本性问题必须解决，那就是我们究竟需要更多数据，还是需要更大的模型？

从某种程度上说，在 2021 到 2023 年这段时间，数据资源远比计算资源来得充裕，因此我们当时完全不必担心数据总量不足的问题，于是计算资源就成了唯一的制约因素，训练预算中的总浮点运算量（FLOPs）才是真正的资源瓶颈，而这些计算资源其实可以通过多种方法分配使用，既可以用小型模型处理海量数据，也能用巨型模型训练少量数据，全看资源如何调配

在这里插入图片描述

这两种极端做法显然都造成了巨大的资源浪费，用微型模型处理海量数据收效甚微，反之亦然，这种资源错配毫无意义，即便是配备 10 个 token 的巨型模型，实际效用同样微乎其微，这成为困扰众多研究者的核心难题。为此，多位学者不约而同地提出了数据与模型的联合缩放定律，试图破解这一难题，到目前为止，我们讨论的缩放定律都只涉及单一变量，这个变量本身也经历了演变，有时是参数量，有时是数据量，有时则是计算量，但我们尚未探讨过联合扩展的情况

数据与模型的联合缩放定律通常呈现如下形态

在这里插入图片描述

这两个方程在一阶近似下功能等价，共同揭示了数据规模与模型参数量之间的取舍关系，Rosenfeld 提供的公式表明：模型误差中有一部分会随数据量呈多项式衰减，而另一部分误差则随模型规模呈多项式衰减，此外还存在一个固有误差项，即便将数据规模和模型容量都扩展到无限大，这个误差依然无法消除

Kaplan 的研究也得出了相同结论，但此处他们关注的是不可消除的误差，而非可优化误差，因此这里并不存在恒定误差项。这种设定看起来有些随意，因为从理论层面来看，并没有必然理由能证明这种函数形式就是唯一正确的表达方式

但令人惊讶的是，这种设定对实际数据和模型中观察到的综合误差具有极佳的拟合效果：

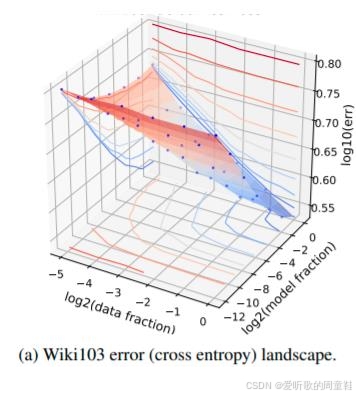
在这里插入图片描述

这个观点源自 Rosenfeld 的研究，他们用精美的三维图展示了数据量的变化趋势，横轴表示模型规模，纵轴则表示损失函数值，这个拟合曲线正是他们提出的函数表达式，散点代表他们的实验数据点，这个拟合曲面几乎完美贴合了所有数据点，尽管这个函数表达式看起来有些随意，像是凭空想出来的，但它的拟合精度却出人意料地高

在这里插入图片描述

这个同样来自 Rosenfeld 的研究，他们的做法是仅用规模较小的前半段数据进行训练，即小模型配合小数据量，因此在图中左下角这个区域（使用小模型和小数据训练）我们可以外推预测更大规模模型配合更多数据训练，这个联合外推的拟合效果究竟如何呢？从图中来看，效果确实相当不错，横坐标代表误差的实际值，而纵坐标则对应着误差的预测值，无论是在 ImageNet 还是 WikiText 数据集上，预测值与实际值几乎完全吻合，这个结果看起来相当理想

在固定计算预算的前提下，我们还能采取哪些优化措施呢？回顾 Kaplan 等人的研究，我们会发现他们在此采用了相似的优化思路

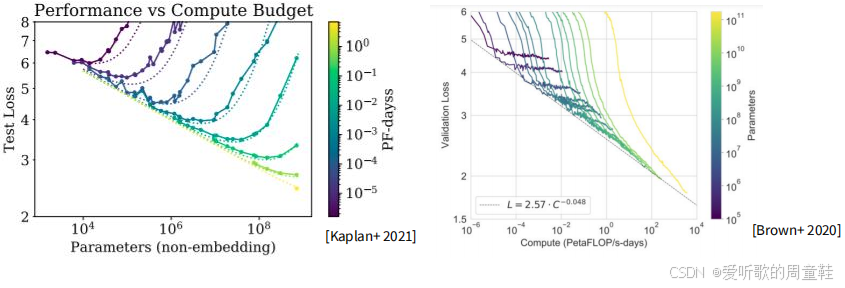
在这里插入图片描述

我们观察到计算资源与数据规模正在协同扩展，在这个分析中，参数量被设定为横坐标，颜色梯度对应计算量大小，因此，为了调节总计算量，这里还隐含着第三个变量维度—数据量，当沿着这些曲线移动时，参数量发生变化而计算量保持恒定，这意味着数据量会相应调整

相信大家对 Chinchilla 模型都有所耳闻，它堪称解决这类计算优化问题的标杆之作，Rosenfeld 与 Kaplan 共同提出了这种联合缩放函数形式，随后他们发现，可以利用这些函数形式以多种方式优化计算量与数据量之间的取舍关系，但受多重因素影响，这些函数形式本身难以精确拟合，而诸如学习率变化曲线等关键细节又至关重要，因此 Kalpan 最初的估算值，某种程度上说与后来验证的最优解存在显著偏差

在这里插入图片描述

谷歌团队发表的 Chinchilla 论文正是为了通过实证研究，精确确定模型参数量与训练数据量之间的最优配比，在训练浮点运算量最小化的前提下，他们采用了三种不同的方法（图中 Approach 1/2/3）通过拟合不同曲线来进行缩放定律预测，这些蓝色圆点代表他们实际训练的模型，这些趋势线实质上预测了在不同浮点运算量条件下，模型参数规模的最优解

相比大家都熟悉 Chinchilla 黄金比例，这个比例大约是每参数对应 20 个 token，该比例正是由此得出的结论，若将图中这些数据点统一乘以 20，所得结果大致就是对应的 token 总量，准确地说，用参数规模乘以 20 即可推算出训练所需的 token 总数，因此，将参数规模与该比例相乘，即可计算出所需的浮点运算量

Kaplan 研究结果与 Chinchilla 研究的核心差异在于：前者仅估算出单一的 token 与参数比例，而后者则确立了动态优化的比例关系，其中一个关键原因在于 学习率调度策略的差异，众所周知，我们采用余弦学习率来训练模型，余弦学习率的变化曲线通常呈现如下形态：

学习率先逐步上升，达到峰值后缓慢下降，最终会逐渐冷却，直至降至预设的最低学习率阈值。关于余弦学习率最常令人困惑的一点是：绝不能提前截断其训练周期，使用余弦学习率时，必须完整执行整个训练周期，才能获得有效的模型。必须让模型完整经历冷却阶段直至训练终止，若在训练中途截断模型，这与从头开始训练并在中途采用余弦学习率有本质区别，这也是导致 Kaplan 团队的估算结果与后期 Chinchilla 论文提出的更精确估算值存在显著偏差的因素之一，当然可能还有其它影响因素

3.7 Chinchilla in depth – 3 methods

那么 Chinchilla 论文作者究竟采用了什么方法？他们采用了三种不同的方法来估算模型规模与训练数据量之间的最优平衡点，每种方法都会得出不同的缩放系数，既有针对模型规模的缩放系数，也有针对数据集的缩放系数

在这里插入图片描述

令人意外的是，在前两种方法中，他们得出的模型规模和数据量的缩放系数都是 0.5，而第三种方法给出的估算结果则存在明显差异，或者说略有不同，这个差异大约在 0.03 左右，不过这个问题我们稍后再详细讨论

Kaplan 等人的研究结果与这三种估算方法得出的数值都相去甚远，接下来我们将逐一分析这些方法，这些方法各有其合理之处，虽然这些方法对规模扩展的假设各不相同，但最终得出的估算结果却惊人地接近

Chinchilla 的第一种方法本质上是 取各曲线的最小值，这意味着什么呢？简单来说，就是将你掌握的所有不同训练曲线叠加在一起

如图所示，横轴代表不同的浮点运算量（FLOPs），纵轴则对应训练损失值，这里展示了多种不同规模模型的训练结果，当然，每种规模的模型都会使用不同数量的训练 token 进行训练，因此在训练过程中，它们最终达到的总浮点运算量也会各不相同

现在我们要做的是观察图中的下边界线，它代表了在任何计算预算下都能达到最优效果的那些关键数据点或检查点，我们可以直接分析这些模型，看看它们实际的参数量级是多少，如图所示，横轴表示总计算量，而参数量与对应的 token 数之间呈现出相当规整的缩放规律，这就是所谓的最小包络法

这本质上表明当我们对所有模型规模进行优化时，预期能达到的最小训练损失实际上在浮点运算量 FLOPs 方法也是最优的。这其实呼应了早期的一些研究论文，回顾 Kaplan 早期论文和其他关于缩放定律的研究，你会发现这种方法早已被采用

可以看到不同规模的模型经过训练，其参数量和计算量各有差异，我们从中选取最小值作为基准，而我们已经发现，这种最小值构成了缩放定律的基础形态，这一结论基于以下发现：在众多不同计算规模下的训练曲线中，最小值始终遵循幂律关系，基于这个假设，我们就能得到相当吻合的拟合结果，由此得出的估算值与其他研究高度吻合，均为 0.5

而另一种方法可能是最标准的 Chinchilla 分析方式—IsoFLOP 分析：

进行 IsoFLOP 分析时，我们需要选取一系列计算规模作为基准，图中每种颜色代表不同的计算量级，具体操作是：针对每个计算规模，既可以训练参数量较小但数据量较大的模型，也可以训练参数量较大但数据量较小的模型，因此，我们针对每个浮点运算量级，系统性地遍历不同的模型规模，这样就能观察每条曲线的最低点

具体可采用两种方式：直接通过非参数方法选取最低点，或者为每条曲线拟合二次函数后求取极值点，但无论采用哪种方法，背后的原理都很简单，这些最低点本身应当遵循可预测的缩放定律，因此可以从中推导出每个浮点运算量级对应的最优参数配置，这些就是所有曲线上的最低点集合

同时还能推算出每个浮点运算所需的最优 token 数量，只需将总浮点运算预算除以参数量，就能直接得出这个数值，因此，这两个最优解可以同步求解，可以看到，这种方法再次得出了非常清晰的结果，与第一种方法完全吻合。根据最终确定的 Chinchilla 模型计算预算，最佳参数量应为 630 亿，而该方法给出的最优参数量为 670 亿，两种方法得出的结果相当接近

最后第三种方法得出的结果稍显杂乱，这要追溯到 Rosenfeld 那篇论文的结论，当我们面对 Rosenfeld 提出的 $n^{-\alpha}+m^{-\beta} + C$ 这类函数形式时，最自然的反应就是：直接训练多组不同参数量 $n$ 和数据量 $m$ 的模型，然后进行曲线拟合，直接把这条曲线拟合到模型输出的任何数据上

正如 Rosenfeld 研究所揭示的，这种拟合方法在某种程度上是合理的，图中这些散点就代表着你训练的所有模型，拟合出的曲线就是左侧你看到的这个热力图上色区域，通过这些虚线，我们就能反推出理论上的等浮点运算曲线应该呈现什么形态。但仔细观察就会发现，这里的缩放定律拟合曲线效果确实不同其他图表中的拟合效果那么理想，观察系数就会发现，Chinchilla 方法三给出的模型规模和总 token 数量估计值与其他方法存在显著差异

去年 Epoch AI 的研究人员 [Besiroglu+ 2024] 对这个结果产生了浓厚的兴趣，他们专门尝试复现了方法三，复现过程异常艰难，因为这些训练运行的原始数据已无从获取，他们甚至采取了极端手段，通过分析图表，运用工具从图像中提出数据点的具体数值，凭借这种方法，他们最终成功复现了原始实验结果

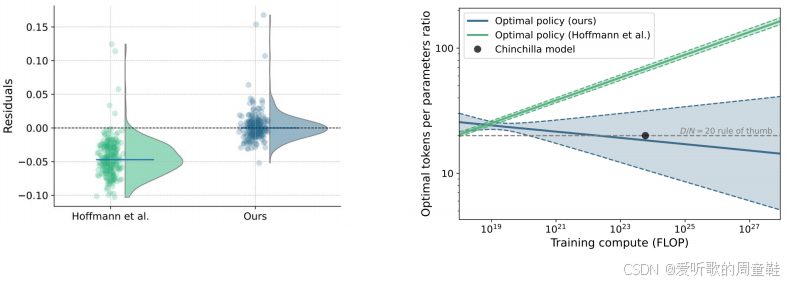
在这里插入图片描述

颇具讽刺意味的是，他们发现问题恰恰出在曲线拟合环节，他们采用的数据和方法本身没有问题，但实际进行曲线拟合时却出现了偏差，因此原始拟合结果存在残差，熟悉回归分析的人都知道，残差应当以零为中心分布，否则就需要通过预测值偏移来实现零中心化，他们发现残差存在非零偏移后，对拟合过程进行了优化改进，经过拟合后，他们的最优估值结果与前两种方法几乎完全吻合

关于 Chinchilla 研究结果的最后一点，我们想探讨的是：我们一直在讨论的训练过程与最优规模配比问题，当你的浮点运算预算固定时，如何训练出最佳性能的模型就成了核心问题

当 Chinchilla 论文和 Kaplan 那篇论文问世时，大语言模型还称不上是成熟的产品，关注点完全在于所有人都只想要打造最大、最炫、最智能的模型，却没人真正在意实际部署这些系统时所需的推理成本。但如今情况完全不同，整个研究范式已经发生了根本性改变，我们真正关注的是推理成本，因为这些系统已经成为实实在在的产品了

因此我们观察到，随着时间的推移，每参数处理的 token 数确实在持续增长：

GPT3 – 2 tokens / param
Chinchilla – 20 tokens / param
LLaMA65B – 22 tokens / param
Llama 2 70B – 29 tokens / param
Mistral 7B – 110 tokens / param
Llama 3 70B – 215 tokens / param

GPT3 的参数效率是每参数处理 2 个 token，而 Chinchilla 将这个指标提升到了每参数处理 20 个 token，此后一段时间内，业界普遍采用每参数处理 20 个 token 的标准进行模型优化，但很快人们就意识到，我们真正追求的是在极小参数量下实现卓越的智能表现，于是业界开始以惊人的速度提升每参数处理的 token 数量，毕竟相比持续为庞大昂贵的推理运算买单，人们更愿意承担前期的一次性训练成本

3.8 Recent example for different (diffusion) models

最后我们以一个有趣的补充作为结尾，对于一个全新的模型架构，文本扩散模型 [Gulrajani+ 2023]，我们至今仍未确定最佳的 token 与参数配比，我们甚至无法确定这个模型是否具备可靠的扩展性，这完全是一种全新的生成式模型范式，然而事实证明，只需沿用同样的分析框架，比如对自回归模型进行等浮点运算分析，我们就能毫不费力地复现出几乎与 Chinchilla 完全吻合的结果

在这里插入图片描述

对扩散模型进行同样的分析时，令人惊讶的是，尽管这完全是另一种生成模型，我们依然观测到了极为相似的曲线规律，若将这些曲线的最小值绘制成图，两者呈现出高度可预测的扩展规律，仅存在一个恒定的偏移量

通过这个随机案例我们想要说明的是这些缩放定律的普适性远超精心挑选的特例，当开发者探索新模型时，这些规律往往会自然而然地显现

4. Recap: scaling laws – surprising and useful!

OK，让我们把这些最后地要点整合起来，对数线性关系不仅适用我们通常考虑的一维数据场景，这种关系同样适用于模型参数维度，它还能延伸到总体计算量层面，因此，我们能够基于此制定各种超参数及其他关键决策，这是第一部分的核心内容

同时，这种规律还能帮助我们实现更智能的资源调配取舍，这让我们能够在大型模型与更多数据之间做出取舍，这一点在 Chinchilla 模型的分析中得到了印证。令人惊叹的是，像等浮点运算分析这样的研究竟能得出如此清晰的结论

以上就是关于基础数据与基础缩放定律的全部内容，今天我们回顾了 Kaplan 和 Chinchilla 的研究成果，希望大家已经理解了这个核心理念：通过数据规模调整、模型规模调整以及运用缩放定律，无需实际进行大规模训练，就能优化模型的各个维度

OK，以上就是本次讲座的全部内容了

结语

本讲我们主要讲解了 缩放定律（Scaling Laws）在大模型设计中的核心作用，内容涵盖缩放定律的理论背景、数据与模型的扩展规律、联合缩放定律（model–data scaling）、Chinchilla 优化原理以及工程上如何利用缩放定律节省训练成本、指导模型设计等关键问题。

在 缩放定律的动机与背景 小节中，课程指出缩放定律允许我们 仅训练数量级更小的模型，就能预测大模型的最优结构、最优训练数据量与下降曲线—从而避免“盲目堆算力”的低效方式。这种思路本质上继承了机器学习理论关于样本复杂度与误差收敛的经典规律，并通过实证方法建立了数据规模、模型规模与训练损失之间高度稳定的幂律关系。

在 数据缩放定律 小节中，我们从 Hestness、Kaplan 等人的经典研究出发，展示了语言建模、语音、机器翻译等任务中普遍存在的规律：
当我们扩大训练数据规模时，测试损失与数据量 n 之间呈对数线性关系，即误差 $≈n−α\approx n^{-\alpha}$ 。我们还讨论了数据重复、多轮次训练的有效样本量衰减问题，指出“数据质量与数据量之间的取舍”可以通过缩放定律来正式建模，并用于预测最优数据混合比例或判断是否应该重复数据。

在 模型缩放和超参数 小节，我们重点解释了缩放定律如何指导大模型的 最优训练配置。核心结论是：在固定计算量下，模型规模与训练 token 数应按 IsoFLOP 曲线 成比例扩展，这正是 Chinchilla 结论 的基础。我们展示了如何利用小规模实验拟合出联合幂律误差模型，从而预测更大模型的最优 token 数、训练步数与 batch 大小，使训练从经验驱动转变为可计算推导。我们想要重点阐述的是 缩放定律让大模型训练从拍脑袋走向可预测、可规划，并能显著减少计算浪费。

整个讲解非常通俗易懂，大家感兴趣的可以看看

下节课我们将深入探讨模型推理的细节，敬请期待🤗

参考

https://stanford-cs336.github.io/spring2025
https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_
https://github.com/stanford-cs336/spring2025-lectures
https://stanford-cs336.github.io/spring2025-lectures/blob/lecture_09-Scaling_laws_basics.pdf

查看全文

http://www.dtcms.com/a/618398.html