信息学与容斥

容斥

计算公式

设集合为 $S_1\sim S_n$，$\mid S\mid$ 表示集合 $S$ 的大小。
$$\mid {\cup }_{i=1}^n{S}_i\mid =\sum _{m=1}^n(-1{)}^{m-1}\sum _{a_i<a_{i+1}}\mid {\cap }_{i=1}^m{S}_{a_i}\mid$$

使用场景

容斥原理常用于集合计数问题。

而枚举集合则可以用二进制枚举。设共有 $n$ 个集合，那么可以用 $2^n$ 的时间复杂度枚举所有可能的集合组合。显然要求是 $n$ 并不大。

注意到基本上容斥的系数为 $\pm 1$ 与枚举的集合组合的集合个数的奇偶性有关，所以可以设计一个函数专门用来计算一个数（二进制枚举）二进制下的 $1$ 的个数。

详细地，给份枚举集合组合的代码。

int num1(int s)//计算s在二进制下的1的个数
{int ans=0;while(s){if(s&1)++ans;s>>=1;}return ans;
}
void Main()
{FUP(base,1,(1<<n)-1)//这里一共有n个集合{ljl opt=(num1(base)&1?-1ll:1ll),cnt=0ll;//这里的+-1因题而异FUP(i,0,n-1)if((base>>i)&1)cnt+=g(i+1);//注意是i+1if(s>=cnt)ans=ans+opt*(ljl_is_vegetable);//在上面 ljl_is_vegetable 处填入集合的值。每题都不一样。}return;
}

例题

洛谷 P1450 [HAOI2008] 硬币购物

先考虑简单版的题目。即没有 $d_i$ 的限制。

不难想到做一个完全背包，令 $f_i$ 表示用所有面值的硬币凑成 $i$ 的方案数。

那么考虑只有一个硬币，且它的限制为 $d_i$。

注意到状态转移方程为 $f_j\leftarrow f_j+f_{j-c_i}$。而其中可能存在不合法的方案。即用了大于 $d_i$ 个 $c_i$。

那么是不是所有 $a+t\cdot c_i=s,t>d_i$ 的都是不合法的，我们只需要 s−ci⋅min⁡{t∣t>di}s-c_i\cdot \min\left\{t\mid t>d_i\right \}s−ci​⋅min{t∣t>di​}，即 $t=d_i+1$ 时的状态。

换句话说，我们需要从不合法方案 $s$ 中剔除至少 $d_i+1$ 个 $c_i$，即 $s-(d_i+1)c_i$。所得的都是不合法的，要减掉。即减掉 $f_{s-(d_i+1)\cdot c_i}$。

所以就可以抽象成一个文氏图。

由于作者很菜很懒，所以用只有 $2$ 个硬币举例。

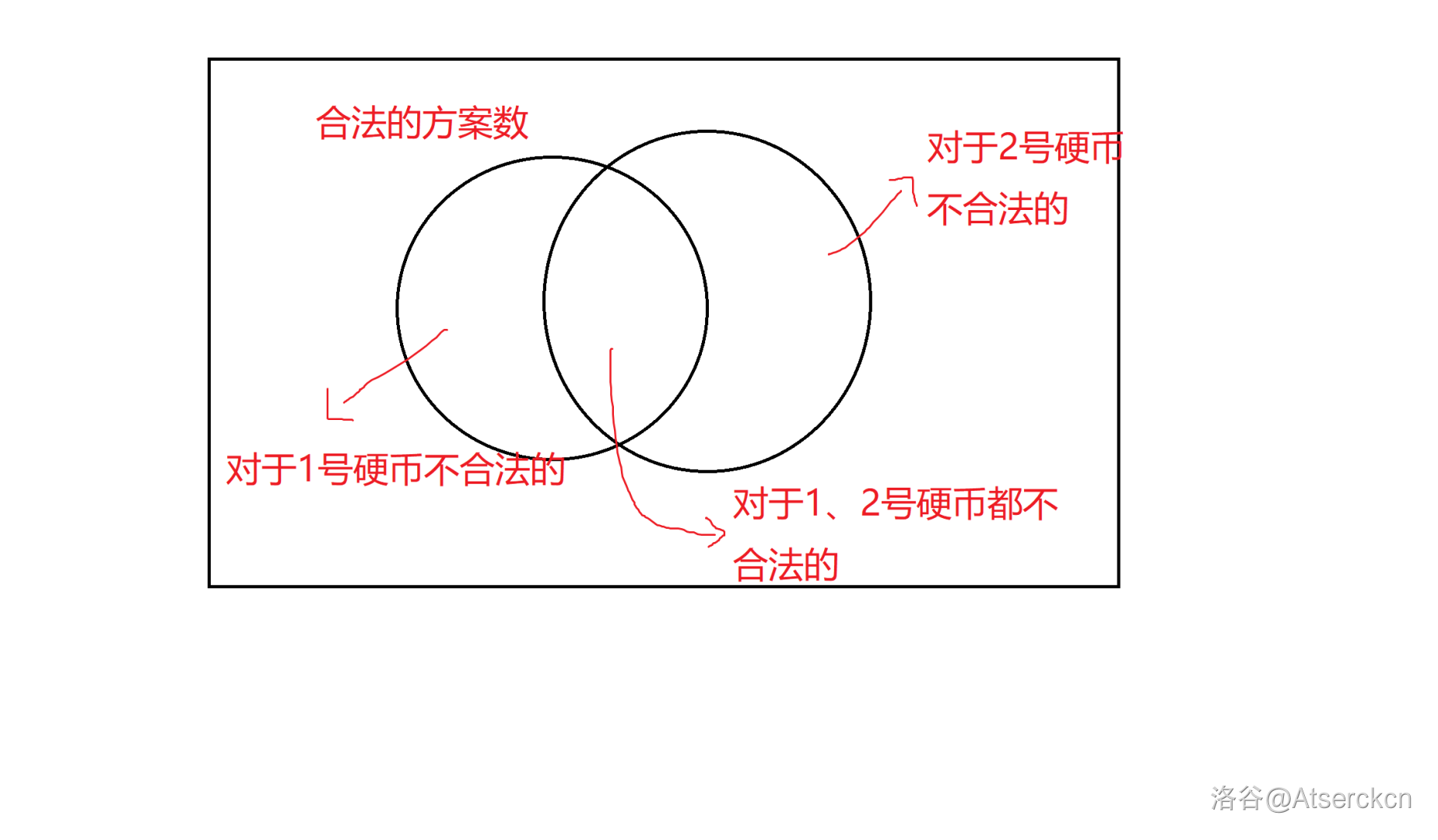
上文中的对于 $i$ 号硬币不合法可以理解为用了至少 $d_i+1$ 个。

我们设左边的圈为 $S_1$，右边的为 $S_2$，全集为 $C$。

那么 $ans=\mid C_{S_1\cup S_2}\mid =\mid C\mid -\mid S_1\mid -\mid S_2\mid +\mid S_1\cap S_2\mid$。

对于多个集合也是同理。

那么再运用上刚说的集合枚举，就可以写出代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
#define FUP(i,x,y) for(int i=(x);i<=(y);++i)
#define FDW(i,x,y) for(int i=(x);i>=(y);--i)
const int S=1e5+5;
int T;
ljl f[S],ans,c[5],d[5],s;
ljl g(int x){return (ljl)c[x]*(d[x]+1);}
int num1(int s)
{int ans=0;while(s){if(s&1)++ans;s>>=1;}return ans;
}
void Main()
{FUP(i,1,4) cin>>d[i];cin>>s;ans=f[s];
//	cout<<"ans="<<ans<<'\n';FUP(base,1,(1<<4)-1){//1-2+
//		cout<<"base "<<base<<'\n';ljl opt=(num1(base)&1?-1ll:1ll),cnt=0ll;
//		cout<<"opt="<<opt<<'\n';FUP(i,0,3)if((base>>i)&1)cnt+=g(i+1);if(s>=cnt)ans=ans+opt*f[s-cnt];}cout<<ans<<'\n';return;
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);FUP(i,1,4)cin>>c[i];cin>>T;f[0]=1ll;FUP(i,1,4)FUP(j,c[i],100000)f[j]+=f[j-c[i]];while(T--)Main();return 0;
}