当前位置： 首页 > news >正文

数据结构：双向链表（2）

news 2025/11/17 5:58:11

目录

 前言 

一、实现双向链表

1.双向链表查找

 2.双向链表在指定位置插入

双向链表在指定位置之后插入

双向链表在指定位置之前插入

 3.双向链表指定位置删除

4.总代码展示：(加入了测试代码)

二、顺序表与链表的分析

一、相同点

二、不同点（核心差异）

三、关键结论

三、链表算法题

一、移除链表元素

 二、反转链表

    总结

 前言 

  上一篇文章讲解了双向链表概念与结构，实现双向链表（双向链表的初始化，双向链表的尾插，双向链表的头插，双向链表的尾删，双向链表的头删）等知识的相关内容，其中实现双向链表其余部分，顺序表与链表的分析，链表算法题为本章节知识的内容。

一、实现双向链表

1.双向链表查找

双向链表的查找操作与单链表类似，但可利用创建一个暂时的指针实现遍历。

函数形式：

ListNode* LTFind(ListNode* h, type x)；

实现：

ListNode* LTFind(ListNode* h, type x)
{if (LTEmpty(h)){return NULL;}ListNode* p = h->next;while (p != h){if (p->data == x){return p;}p = p->next;}return NULL;
}

细讲：

 if (LTEmpty(h)) {return NULL;}// 3. 遍历查找目标节点（从第一个数据节点开始）ListNode* p = h->next;while (p != h) {  // 双向循环链表：遍历至回到头节点结束if (p->data == x) {return p;  // 找到目标，返回节点指针}p = p->next;}// 4. 遍历完未找到return NULL;

通过遍历来实现，如果在遍历过程中找到了我们需要查找的数据就返回当前位置的节点，没有就返回空。

 2.双向链表在指定位置插入

双向链表在指定位置插入分为双向链表在指定位置之前插入与双向链表在指定位置之后插入：

双向链表在指定位置之后插入

函数形式：

void LTInsert(ListNode* pos, type x)

实现：

void LTInsert(ListNode* pos, type x)
{assert(pos);ListNode* p = pos->next;ListNode* newnode = LTcreat(x);pos->next = newnode;newnode->prev = pos;newnode->next = p;p->prev = newnode;
}

细讲：该函数用于在双向链表的 指定节点 pos 之后插入新节点，核心逻辑是通过调整指针关系实现无缝插入。

1.参数与前置检查

void LTInsert(ListNode* pos, type x) {  // type需替换为实际数据类型（如int）assert(pos);  // 断言：确保pos不为空指针，避免操作无效节点
  • 作用：pos 是插入位置的基准节点（新节点将插入其后），x 是新节点的数据。
  • 风险控制：assert(pos) 防止用户传入 nullptr 导致后续操作崩溃。

2. 保存后继节点

    ListNode* p = pos->next;  // 临时保存pos的原后继节点
  • 必要性：插入新节点后，pos 的 next 指针会指向新节点，若不提前保存原后继 pos->next，将导致原链表后半部分丢失。

 核心：调整指针关系（4步插入法）

    pos->next = newnode;       // 步骤1：pos的后继指向新节点newnode->prev = pos;       // 步骤2：新节点的前驱指向posnewnode->next = p;         // 步骤3：新节点的后继指向原后继pp->prev = newnode;         // 步骤4：原后继p的前驱指向新节点

在指定位置之后的插入操作其实也没有很难，还是先断言，后续就是先申请一个新节点，跟头插尾插相似的方式。

双向链表在指定位置之前插入

函数形式：

void LTInsertfront(ListNode* pos, type x);

实现：

void LTInsertfront(ListNode* h, ListNode* pos, type x)
{if (LTEmpty(h)){return ;}ListNode* p = h;while (p->next != h){if (p->next == pos){break;}p = p->next;}if (p->next == h){return;}ListNode* newnode = LTcreat(x);ListNode* pr = p->next;newnode->next = pr;newnode->prev = p;p->next = newnode;pr->prev = newnode;
}

细讲：核心功能是 在指定节点 pos 的前驱位置插入新节点（即“在 pos 前面插入”）。

void LTInsertfront(ListNode* h, ListNode* pos, type x){  // type替换为实际数据类型（如int）if (LTEmpty(h)) {return;}// 2. 查找pos的前驱节点pListNode* p = h;while (p->next != h) {  // 遍历所有有效节点（不包含头节点h）if (p->next == pos) {break;  // 找到pos，p是pos的前驱}p = p->next;}// 3. 校验pos是否存在（未找到则退出）if (p->next == h) {return;}// 4. 创建并插入新节点ListNode* newnode = LTcreat(x);ListNode* pos_node = p->next;  // pos_node = pos，明确变量含义newnode->prev = p;newnode->next = pos_node;p->next = newnode;pos_node->prev = newnode;
}

 3.双向链表指定位置删除

删除节点需修改 前驱节点的 next 和 后继节点的 prev，并释放被删节点内存。关键是 处理边界情况（如 pos 是头/尾节点）。

函数形式：

void LTErase(ListNode* pos)

实现：

void LTErase(ListNode* pos)
{assert(pos);ListNode* p = pos->prev;p->next = pos->next;pos->next->prev = p;free(pos);pos = NULL;
}

细讲：

  • 步骤：
    1. 通过 pos->prev 获取前驱节点 p；
    2. 调整指针：p->next = pos->next（切断 p 与 pos 的连接，指向 pos 的后继）；
    3. 调整后继节点的前驱指针：pos->next->prev = p（切断后继与 pos 的连接，指向 p）；
    4. 释放 pos 节点内存，并置空局部指针 pos。

  • 前置断言 assert(pos)

  • 作用：确保 pos 不为空指针，避免后续 pos->prev 等操作引发崩溃。

4.总代码展示：(加入了测试代码)

1.h

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int type;
typedef struct ListNode
{type data;//前驱指针,指向前一个指针struct ListNode* prev;//后继指针，指向后一个指针struct ListNode* next;
}ListNode;
void LTInit(ListNode** h);
void LTPushBack(ListNode* h, type x);
ListNode* LTcreat(type x);
void LTPushFront(ListNode* h, type x);
void LTPopBack(ListNode* h);
void LTPopFront(ListNode* h);
void LTDestory(ListNode* h);
void print(ListNode* h);
ListNode* LTFind(ListNode* h, type x);
void LTInsert(ListNode* pos, type x);
void LTInsertfront(ListNode* h,ListNode* pos, type x);
void LTErase(ListNode* pos);

1.cpp

#include"1.h"void LTInit(ListNode** h)
{     ListNode* ph = (ListNode*)malloc(sizeof(ListNode));if (ph == NULL){perror("malloc fail!");exit(1);}*h = ph;(*h)->data = -1;(*h)->next = *h;(*h)->prev = *h;
}
ListNode* LTcreat(type x)
{ListNode* ph = (ListNode*)malloc(sizeof(ListNode));if (ph == NULL){perror("malloc fail!");exit(1);}ph->data = x;ph->next = ph;ph->prev = ph;return ph;
}
void LTPushBack(ListNode* h, type x)
{     ListNode* p = LTcreat(x);p->next = h;p->prev = h->prev;h->prev->next = p;h->prev = p;
}
void LTPushFront(ListNode* h, type x)
{ListNode* p = LTcreat(x);p->next = h->next;p->prev = h;h->next->prev = p;h->next = p;
}
bool LTEmpty(ListNode* phead)
{assert(phead);return phead->next == phead;
}
void LTPopBack(ListNode* h)
{if (LTEmpty(h)){return;}ListNode* p = h->prev;h->prev = p->prev;p->prev->next = h;free(p);
}
void LTPopFront(ListNode* h)
{if (LTEmpty(h) ){printf("链表为空，无法头删\n");return;}ListNode* p = h->next;h->next = p->next;p->next->prev = h;free(p);
}
void LTDestory(ListNode* h)
{if (LTEmpty(h)){free(h);return;}ListNode* p = h->next;while (p != h){ListNode* pr = p;p = p->next;free(pr);}free(h);h = NULL;
}
void print(ListNode* h)
{if (LTEmpty(h)){return;
}ListNode* p = h->next;while (p != h){printf("%d ", p->data);p = p->next;}printf("\n");
}
ListNode* LTFind(ListNode* h, type x)
{if (LTEmpty(h)){return NULL;}ListNode* p = h->next;while (p != h){if (p->data == x){return p;}p = p->next;}return NULL;
}
void LTInsert(ListNode* pos, type x)
{assert(pos);ListNode* p = pos->next;ListNode* newnode = LTcreat(x);pos->next = newnode;newnode->prev = pos;newnode->next = p;p->prev = newnode;
}
void LTInsertfront(ListNode* h, ListNode* pos, type x)
{if (LTEmpty(h)){return ;}ListNode* p = h;while (p->next != h){if (p->next == pos){break;}p = p->next;}if (p->next == h){return;}ListNode* newnode = LTcreat(x);ListNode* pr = p->next;newnode->next = pr;newnode->prev = p;p->next = newnode;pr->prev = newnode;
}
void LTErase(ListNode* pos)
{assert(pos);ListNode* p = pos->prev;p->next = pos->next;pos->next->prev = p;free(pos);pos = NULL;
}

main.cpp

#include"1.h"
void test()
{ListNode* h;LTInit(&h);LTPushBack(h, 10);    //10 LTPushBack(h, 15);    //10 15 LTPushBack(h, 111);   //10 15 111print(h);LTPushFront(h, 2);     //2 10 15 111LTPushFront(h, 12);    //12 2 10 15 111print(h);LTPopBack(h);         // 12 2 10 15print(h);LTPopFront(h);        //2 10 15print(h);ListNode* p = LTFind(h,10);LTInsert(p, 100);	//2 10 100 15print(h);LTInsert(p, 200);	//2 10 200 100 15print(h);LTErase(p);print(h);            //2 200 100 15LTDestory(h);
}int main()
{test();
}

二、顺序表与链表的分析

本图列举了顺序表与链表之间的相同点与不同点：

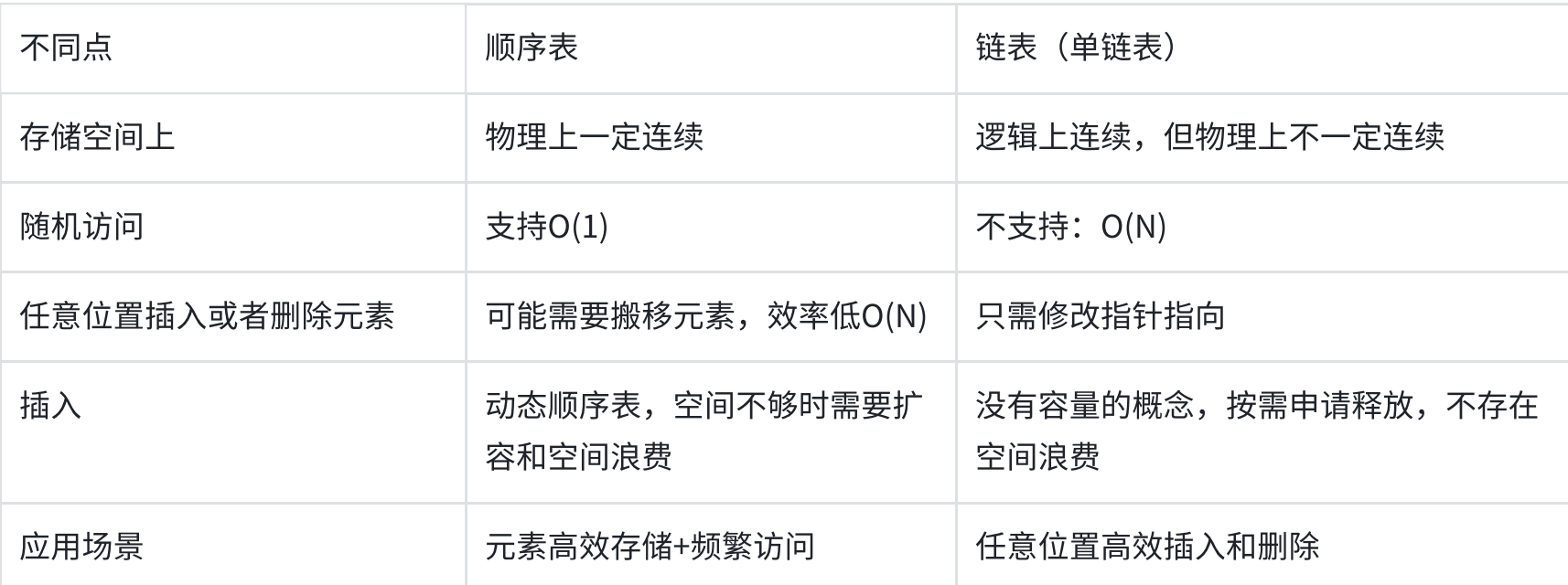
一、相同点
  • 逻辑结构一致：均为线性表，数据元素之间呈一对一的顺序关系。
  • 核心操作相同：都支持插入、删除、查找、遍历等基本线性表操作。
  • 存储数据类型：均可存储相同类型的数据元素（如整数、结构体等）。
二、不同点（核心差异）
对比维度顺序表链表
存储结构连续内存空间（数组实现）非连续内存空间（节点通过指针/引用连接）
内存分配方式静态分配（固定大小）或动态分配动态分配（节点按需申请释放）
访问效率随机访问（通过下标 O(1)）顺序访问（需从头遍历 O(n)）
插入/删除效率中间/头部插入删除需移动元素（O(n)）仅需修改指针（O(1)，已知前驱节点时）
空间利用率可能存在内存浪费（预分配过大）或溢出无内存浪费（按需分配），但额外存储指针
实现复杂度简单（依赖数组）复杂（需管理指针/引用，避免内存泄漏）
三、关键结论
  • 顺序表：适合 频繁随机访问、数据量固定 的场景（如存储学生信息表）。
  • 链表：适合 频繁插入删除、数据量动态变化 的场景（如实现队列、栈）。

三、链表算法题

一、移除链表元素

移除链表元素

203. 移除链表元素 - 力扣（LeetCode）

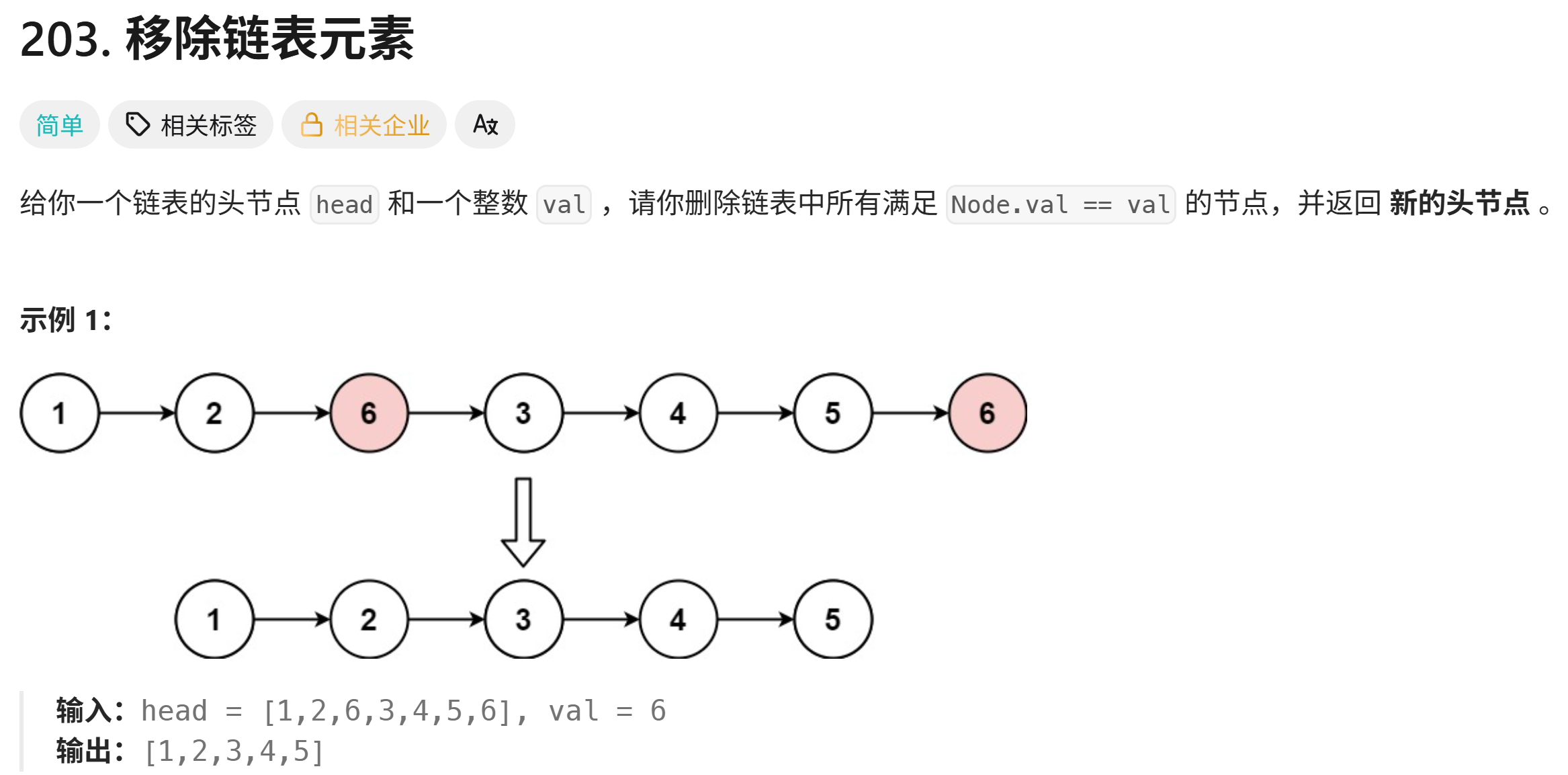
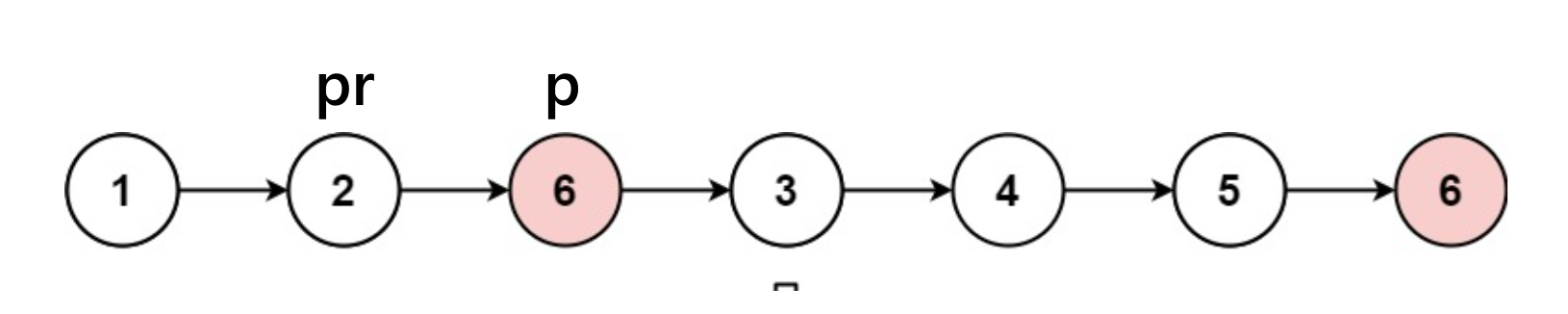
由题意可知，本题要求移除值为val的节点，并要求返回新的头结点：

  • 1.链表的解法可以通过遍历整个链表，用一个节点存储前一个节点，在发现值为val时候改变next区域的指向解答：
  • 2.我们也可以选择创建一个新链表，存储符合要求的节点，虽然没有释放原链表空间，但做OJ题不释放也没什么问题的，该方法较为简单，本次解题选择此方法：

解题代码：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/typedef struct ListNode Node; 
struct ListNode* removeElements(struct ListNode* head, int val) 
{ Node *h=NULL,*pr=NULL;
Node * p=head;
while(p)
{if(p->val!=val){  if(h==NULL){h=p;pr=p;}
else 
{pr->next=p;pr=p;
}}p=p->next;
}
if(pr)pr->next=NULL;return h; 
}

解题思路：

// 定义链表节点结构体（题目已给出）
struct ListNode {int val;struct ListNode *next;
};// 简化结构体名称为 Node（方便后续使用）
typedef struct ListNode Node; // 主函数：移除值为 val 的节点
struct ListNode* removeElements(struct ListNode* head, int val) { Node *h = NULL;  // 新链表的头节点（待返回）Node *pr = NULL; // 新链表的尾节点指针（用于拼接有效节点）Node *p = head;  // 遍历原链表的指针// 遍历原链表while (p) {// 当前节点值不等于 val，需保留到新链表if (p->val != val) {  if (h == NULL) {  // 新链表为空（首次遇到有效节点）h = p;       // 新链表头节点指向当前节点pr = p;      // 新链表尾节点也指向当前节点} else {          // 新链表非空（拼接后续有效节点）pr->next = p; // 尾节点 next 指向当前节点（拼接）pr = p;       // 尾节点指针后移到当前节点}}p = p->next; // 遍历下一个节点（无论当前节点是否保留）}// 遍历结束后，新链表尾节点 next 置空（避免野指针）if (pr) pr->next = NULL;return h; // 返回新链表头节点
}

1.变量初始化

  • h：新链表的头节点，初始为 NULL（表示新链表为空）。
  • pr：新链表的尾节点指针，用于拼接有效节点（值不等于 val 的节点）。
  • p：遍历指针，从原链表头节点 head 开始，依次访问每个节点。

2. 遍历原链表（while (p)）

循环条件 p 等价于 p != NULL，即遍历至原链表末尾时停止。

  • 情况1：当前节点 p 的值不等于 val（需保留）

    • 首次保留节点（h == NULL）：
      新链表为空，因此 h（头节点）和 pr（尾节点）都指向当前节点 p。
    • 非首次保留节点（h != NULL）：
      通过 pr->next = p 将当前节点 p 拼接到新链表尾部，然后 pr = p 更新尾节点指针。

  • 情况2：当前节点 p 的值等于 val（需删除）
    不执行任何操作（不拼接至新链表），直接通过 p = p->next 跳过当前节点。

3. 处理新链表尾节点（if (pr) pr->next = NULL）

  • 遍历结束后，pr 指向新链表的最后一个有效节点。
  • 若新链表非空（pr != NULL），需将其 next 置为 NULL，避免原链表中后续节点（已删除节点）的指针残留，导致野指针风险。

4. 返回新链表头节点

h 指向新链表的第一个有效节点，若原链表所有节点都被删除（如 head = [2,2,2], val=2），则 h 保持 NULL，返回空链表。

 二、反转链表

反转链表

206. 反转链表 - 力扣（LeetCode）

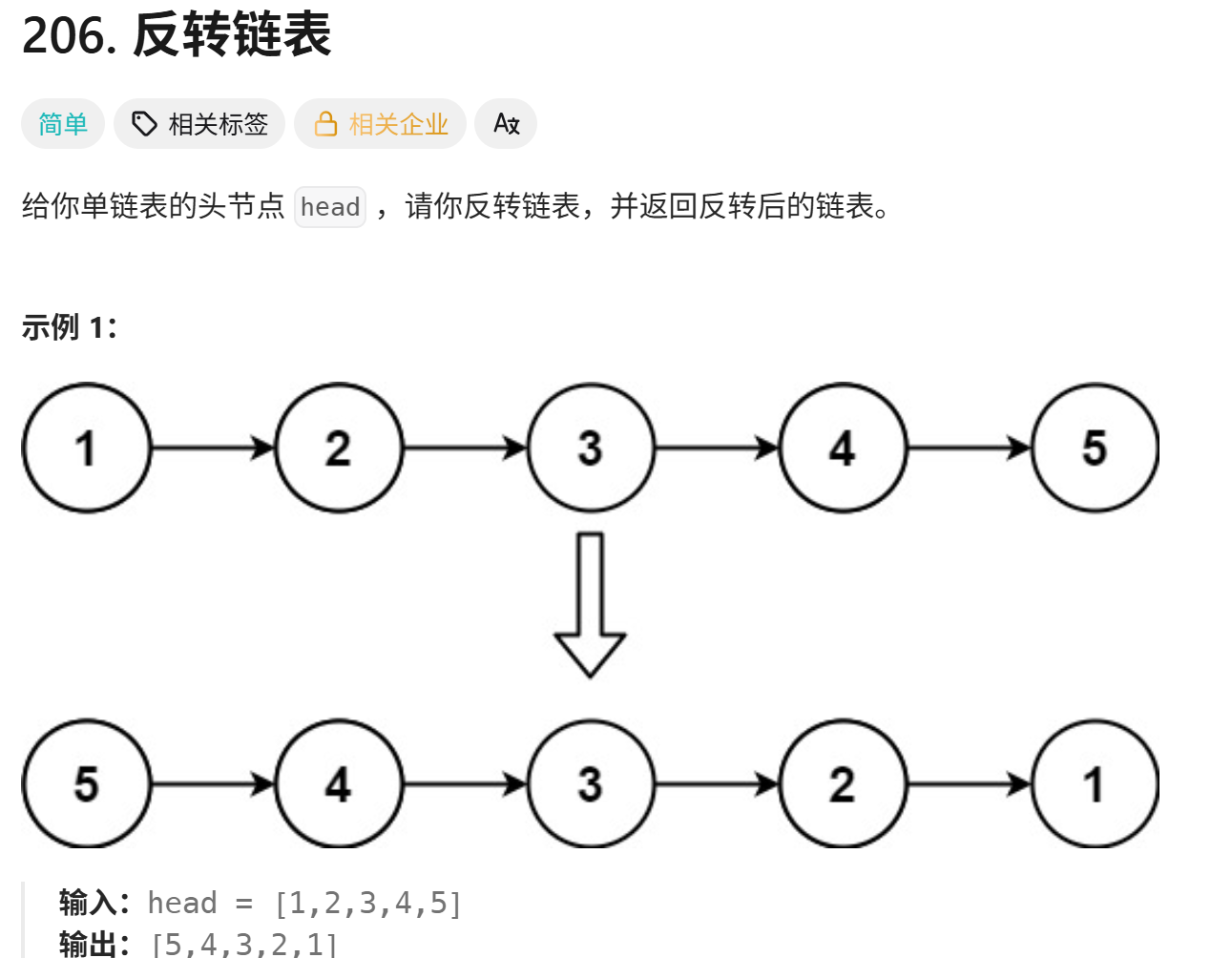
解题思路:

  • 反转题中给出的链表，如果简单来想，我们可以创建一个新链表一个一个节点的复制，但是题中的是单链表，不可找到前驱节点的，如果用上面思路，那会相当麻烦了。
  • 正确思路：通过三个指针来实现：

  • 迭代法（推荐：时间O(n)，空间O(1)）

    核心思路：

    通过 3个指针 遍历链表，逐次反转节点指向：

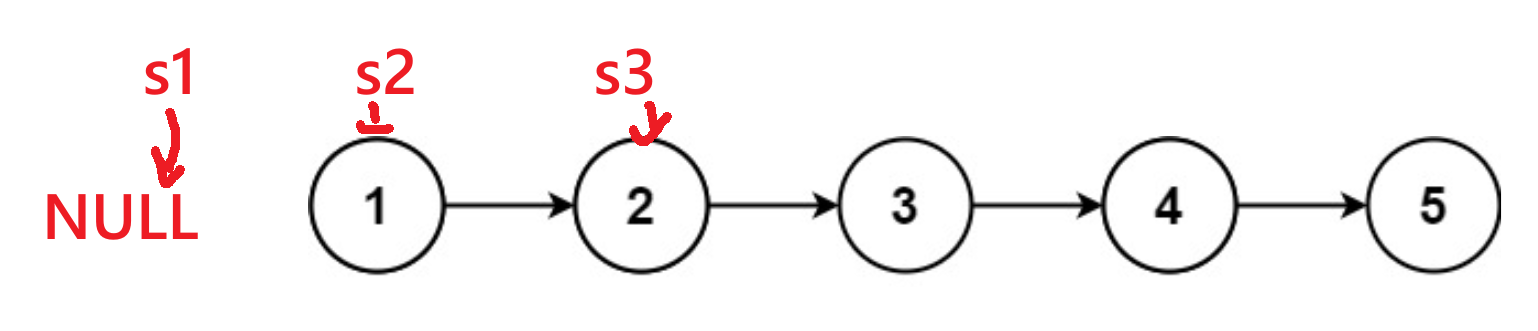
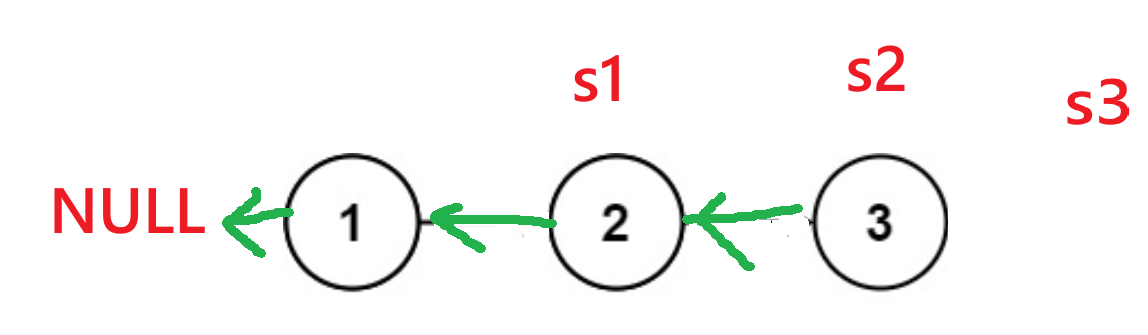
  • prev：指向 已反转部分 的头节点（初始为 NULL）。
  • curr：指向 当前待反转节点（初始为 head）。
  • next：临时保存 curr 的下一个节点（避免反转后断链）。

简单来做，我将其命名为s1,s2,s3了。

基本结构是这样的，接下来我将结合代码来讲解:

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/typedef struct ListNode node;
struct ListNode* reverseList(struct ListNode* head)
{  node * s1=NULL;
node *s2=head,*s3=NULL;
if(s2)
{s3=s2->next;
}while(s2){s2->next=s1;s1=s2;s2=s3;if(s3){s3=s3->next;}}  return s1;
}

讲解：

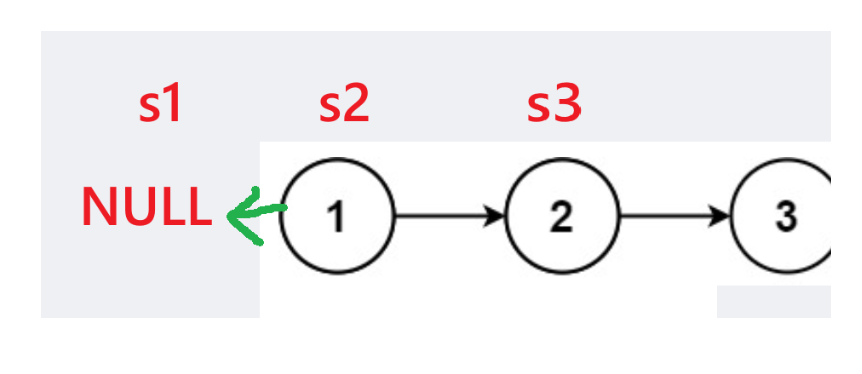
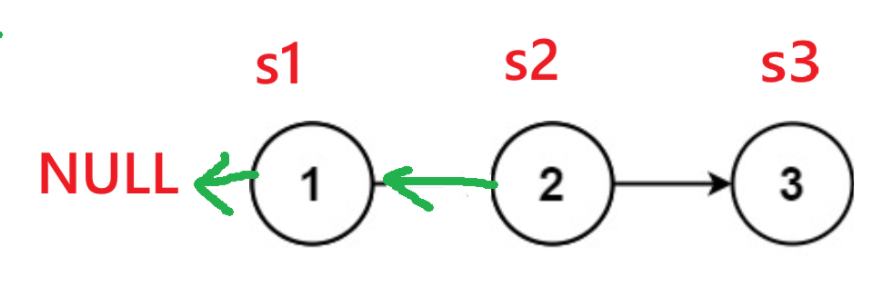
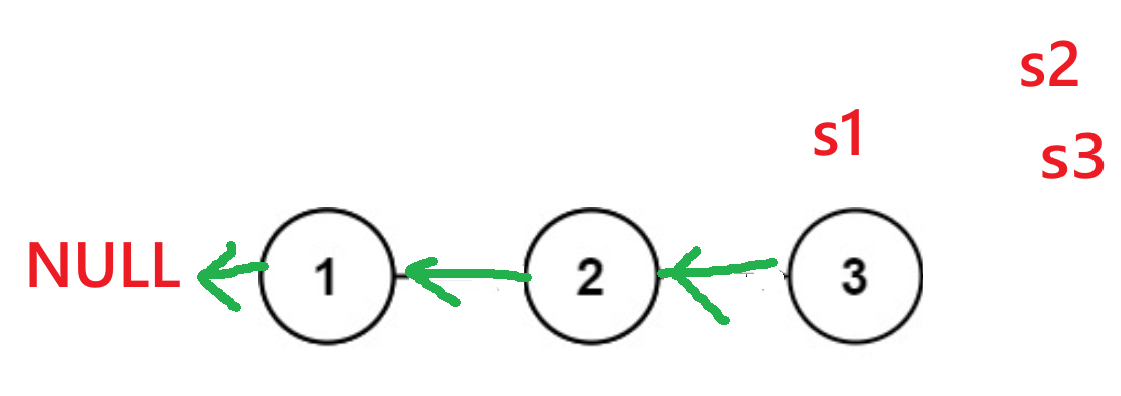
typedef struct ListNode node;  // 简化结构体名称为 node
struct ListNode* reverseList(struct ListNode* head) {  node *s1 = NULL;           // s1：指向「已反转部分」的头节点（初始为空，因为还未开始反转）node *s2 = head;           // s2：指向「当前待反转节点」（初始为原链表的头节点）node *s3 = NULL;           // s3：临时保存 s2 的下一个节点（避免反转后链表断链）if (s2) {  // 若 s2（原头节点）不为空，才初始化 s3（避免空链表时访问 NULL->next）s3 = s2->next;  }// ... 循环反转逻辑 ...
}

while (s2) {  // 循环条件：当前待反转节点 s2 不为 NULL（遍历完所有节点后终止）// 步骤1：反转当前节点 s2 的指向（指向已反转部分的头节点 s1）s2->next = s1;  // 步骤2：s1 后移到 s2（已反转部分的长度+1，s1 成为新的“已反转头节点”）s1 = s2;        // 步骤3：s2 后移到 s3（继续处理下一个待反转节点）s2 = s3;        // 步骤4：若 s3 不为空，s3 后移到下一个节点（为下次循环做准备）if (s3) {       s3 = s3->next;  }
}  
return s1;  // 循环结束后，s1 指向原链表的尾节点（即新链表的头节点）

图示：

根据上图：我们可知代码  if (s3) {        s3 = s3->next;  的原因了：

while (s2) {  // 循环条件：当前待反转节点 s2 不为 NULL（遍历完所有节点后终止）
    // 步骤1：反转当前节点 s2 的指向（指向已反转部分的头节点 s1）
    s2->next = s1;  
    // 步骤2：s1 后移到 s2（已反转部分的长度+1，s1 成为新的“已反转头节点”）
    s1 = s2;        
    // 步骤3：s2 后移到 s3（继续处理下一个待反转节点）
    s2 = s3;        
    // 步骤4：若 s3 不为空，s3 后移到下一个节点（为下次循环做准备）
    if (s3) {       
        s3 = s3->next;  
    }
}  
return s1;  // 循环结束后，s1 指向原链表的尾节点（即新链表的头节点）

    总结

  以上就是今天要讲的内容，本篇文章涉及的知识点为：实现双向链表其余部分，顺序表与链表的分析，链表算法题等知识的相关内容，为本章节知识的内容，希望大家能喜欢我的文章，谢谢各位，接下来的内容我会很快更新。

http://www.dtcms.com/a/617574.html

相关文章：

  • Java EE - 常见的死锁和解决方法
  • transformer 教程(一) qkv矩阵介绍以及为什么除以根号d推导
  • 网络网站开发江苏电信网站备案
  • 树莓派 5 上 Ubuntu 24.04 LTS 自带 RDP 远程桌面重启密码就变
  • 算法---贪心算法（Greedy Algorithm）
  • TDengine 字符串函数 REGEXP_IN_SET 用户手册
  • 佛山市外贸网站建设公司因网站开发需要
  • 神经网络组植物分类学习规划与本周进展综述15
  • 做律师事务所网站牡丹江住房和城乡建设厅网站
  • 上海崇明林业建设有限公司 网站建设 市民中心网站
  • 在UEC++中使用什么方式返回像 FTransform 这种类型的值
  • GPT‑OSS‑20B MoE 在昇腾 NPU 上的部署与性能实测：开发者视角的多精度推理优化实践
  • 后端服务弹性伸缩实践实践：让系统更高效、稳定
  • 网站的比较做网站哪家便宜
  • 寻找昆明网站建设手机网站 跳转
  • 建站网址大全56做视频网站
  • jsp网站开发教程响应式布局是什么意思
  • dede中英文企业网站建筑方案设计案例
  • 常见网站颜色搭配技术导航源码
  • 简单响应式网站设计代码翻书效果的网站
  • 网站seo方案建议电影网站怎么做优化
  • 网站开发外包不给ftp外贸推广方式
  • 百度 网站 说明qq是哪家公司运营的
  • 门头设计效果图网站西安学网站开发哪边好
  • 公司网站模板源代码沈阳百度seo
  • 房产网站怎么做才能吸引人怎样做自己网站
  • 不错宁波seo公司网站优化 推广
  • 好的网站首页建设公司网站托管费用 优帮云
  • 企业网站策划方案模板品牌设计网站建设
  • 微科技h5制作网站模板下载网站建设龙卡要审批多久时间