【高级机器学习】 9. 代理损失函数的鲁棒性
Robustness of Surrogate Loss Functions
(代理损失函数的鲁棒性)
机器学习模型的核心目标是通过最小化损失函数 (Loss Function) 来学习一个最优假设 ( h )。
然而,现实中的数据往往存在噪声(noise)与异常值(outliers),这就要求我们选择鲁棒的(robust)损失函数。
本章将介绍不同的代理损失函数(surrogate loss functions),它们对应的噪声分布假设,以及各自的鲁棒性分析。
一、Surrogate Loss Functions
我们常见的几种损失函数如下:
-
Least squares loss(最小二乘损失)
ℓ(X,Y,h)=(Y−h(X))2 \ell(X,Y,h) = (Y - h(X))^2 ℓ(X,Y,h)=(Y−h(X))2 -
Absolute loss(绝对值损失)
ℓ(X,Y,h)=∣Y−h(X)∣ \ell(X,Y,h) = |Y - h(X)| ℓ(X,Y,h)=∣Y−h(X)∣ -
Cauchy loss(柯西损失)
ℓ(X,Y,h)=log2(1+(Y−h(X)σ)2) \ell(X,Y,h) = \log_2\left(1 + \left(\frac{Y - h(X)}{\sigma}\right)^2\right) ℓ(X,Y,h)=log2(1+(σY−h(X))2) -
Correntropy (Welsch) loss(相关熵损失)
ℓ(X,Y,h)=(1−exp(−(Y−h(X)σ)2)) \ell(X,Y,h) = \left(1 - \exp\left(-\left(\frac{Y - h(X)}{\sigma}\right)^2\right)\right) ℓ(X,Y,h)=(1−exp(−(σY−h(X))2))
这些函数都可作为“代理损失”(surrogate loss)用于不同类型的噪声条件下。
直觉:
平方损失对大误差(outlier)极度敏感;而 Cauchy 和 Correntropy 损失能抑制异常点的影响,使模型更鲁棒。
二、Distribution of Noise(噪声分布假设)
假设噪声为
ϵ=Y−h(X)
\epsilon = Y - h(X)
ϵ=Y−h(X)
则不同的损失函数隐含着不同的噪声模型假设:
-
Gaussian 分布(高斯噪声)
p(ϵ∣X,Y,h,β−1)=β2πexp(−βϵ22) p(\epsilon|X,Y,h,\beta^{-1}) = \sqrt{\frac{\beta}{2\pi}} \exp\left(-\frac{\beta\epsilon^2}{2}\right) p(ϵ∣X,Y,h,β−1)=2πβexp(−2βϵ2) -
Laplacian 分布(拉普拉斯噪声)
p(ϵ∣X,Y,h,σ)=12σexp(−2∣ϵ∣σ) p(\epsilon|X,Y,h,\sigma) = \frac{1}{\sqrt{2}\sigma} \exp\left(-\frac{\sqrt{2}|\epsilon|}{\sigma}\right) p(ϵ∣X,Y,h,σ)=2σ1exp(−σ2∣ϵ∣) -
Cauchy 分布(柯西噪声)
p(ϵ∣X,Y,h,γ)=1πγ(1+(ϵ/γ)2) p(\epsilon|X,Y,h,\gamma) = \frac{1}{\pi\gamma\left(1+(\epsilon/\gamma)^2\right)} p(ϵ∣X,Y,h,γ)=πγ(1+(ϵ/γ)2)1
它们之间的区别体现在尾部厚度(tail heaviness)上:
高斯 → 拉普拉斯 → 柯西 的尾部越来越“厚”,对应的鲁棒性也越来越强。
三、Laplacian Regression(最小绝对偏差回归)
假设噪声服从拉普拉斯分布:
p(ϵ∣X,Y,h,σ)=12σexp(−2∣ϵ∣σ)
p(\epsilon|X,Y,h,\sigma) = \frac{1}{\sqrt{2}\sigma} \exp\left(-\frac{\sqrt{2}|\epsilon|}{\sigma}\right)
p(ϵ∣X,Y,h,σ)=2σ1exp(−σ2∣ϵ∣)
对一个样本的似然为:
p(yi∣xi,h,b)=12σexp(−2∣yi−h(xi)∣σ)
p(y_i|x_i,h,b) = \frac{1}{\sqrt{2}\sigma}\exp\left(-\frac{\sqrt{2}|y_i - h(x_i)|}{\sigma}\right)
p(yi∣xi,h,b)=2σ1exp(−σ2∣yi−h(xi)∣)
整个数据集的似然为:
p(S∣X,h,b)=(12σ)n∏i=1nexp(−2∣yi−h(xi)∣σ)
p(S|X,h,b) = \left(\frac{1}{\sqrt{2}\sigma}\right)^n \prod_{i=1}^n \exp\left(-\frac{\sqrt{2}|y_i - h(x_i)|}{\sigma}\right)
p(S∣X,h,b)=(2σ1)ni=1∏nexp(−σ2∣yi−h(xi)∣)
取负对数似然后得到:
−lnp(S∣X,h,b)=nln(2σ)+2σ∑i=1n∣yi−h(xi)∣
-\ln p(S|X,h,b) = n\ln(\sqrt{2}\sigma) + \frac{\sqrt{2}}{\sigma}\sum_{i=1}^n |y_i - h(x_i)|
−lnp(S∣X,h,b)=nln(2σ)+σ2i=1∑n∣yi−h(xi)∣
→ 可见这等价于 最小化绝对误差(L1 Loss)。
四、Cauchy Regression(柯西回归)
假设噪声服从柯西分布:
p(ϵ∣X,Y,h,γ)=1πγ(1+(ϵ/γ)2)
p(\epsilon|X,Y,h,\gamma) = \frac{1}{\pi\gamma\left(1 + (\epsilon/\gamma)^2\right)}
p(ϵ∣X,Y,h,γ)=πγ(1+(ϵ/γ)2)1
则似然函数为:
p(S∣X,h,γ)=(1πγ)n∏i=1n11+(yi−h(xi)γ)2
p(S|X,h,\gamma) = \left(\frac{1}{\pi\gamma}\right)^n \prod_{i=1}^n \frac{1}{1 + \left(\frac{y_i - h(x_i)}{\gamma}\right)^2}
p(S∣X,h,γ)=(πγ1)ni=1∏n1+(γyi−h(xi))21
负对数似然:
−lnp(S∣X,h,γ)=nln(πγ)+∑i=1nln(1+(yi−h(xi)γ)2)
-\ln p(S|X,h,\gamma) = n\ln(\pi\gamma) + \sum_{i=1}^n \ln\left(1 + \left(\frac{y_i - h(x_i)}{\gamma}\right)^2\right)
−lnp(S∣X,h,γ)=nln(πγ)+i=1∑nln(1+(γyi−h(xi))2)
→ 等价于使用 Cauchy Loss:
ℓ(X,Y,h)=ln(1+(Y−h(X)γ)2)
\ell(X,Y,h) = \ln\left(1 + \left(\frac{Y - h(X)}{\gamma}\right)^2\right)
ℓ(X,Y,h)=ln(1+(γY−h(X))2)
五、三种噪声分布对比

从分布曲线来看:
- 高斯分布(红线):中心窄、尾巴快收敛 → 对异常值极敏感。
- 拉普拉斯分布(黑线):稍厚的尾巴 → 更能容忍异常。
- 柯西分布(蓝线):尾部最厚 → 对异常点影响最小。
结论:
噪声分布尾部越“厚”,对应的损失函数越鲁棒。
六、Objective Function(目标函数)
机器学习算法可以形式化为寻找最优假设的映射:
A:S∈(X×Y)n↦hS∈H
\mathcal{A}: S \in (\mathcal{X} \times \mathcal{Y})^n \mapsto h_S \in \mathcal{H}
A:S∈(X×Y)n↦hS∈H
目标是最小化经验风险:
minh∈H1n∑i=1nℓ(Xi,Yi,h)
\min_{h\in H} \frac{1}{n}\sum_{i=1}^n \ell(X_i, Y_i, h)
h∈Hminn1i=1∑nℓ(Xi,Yi,h)
即我们通过优化损失函数来得到最优模型。
七、Optimality Criterion(最优性条件)
定义目标函数:
f(h)=1n∑i=1nℓ(Xi,Yi,h)
f(h) = \frac{1}{n}\sum_{i=1}^n \ell(X_i, Y_i, h)
f(h)=n1i=1∑nℓ(Xi,Yi,h)
点 ( h ) 是最优解,当且仅当:
∇f(h)⊤(h′−h)≥0,∀h′∈domain(f)
\nabla f(h)^\top (h' - h) \ge 0, \quad \forall h' \in \text{domain}(f)
∇f(h)⊤(h′−h)≥0,∀h′∈domain(f)
若定义域无界,则最优性达成于:
∇f(h)=0
\nabla f(h) = 0
∇f(h)=0
换句话说,最优点的梯度为零。
我们也可以将其一维化:
g(t)=f(th)
g(t) = f(th)
g(t)=f(th)
则
g′(t)=∇f(th)⊤h
g'(t) = \nabla f(th)^\top h
g′(t)=∇f(th)⊤h
若 ( h ) 是最小点,则有 ( g’(1)=0 )。
因此,最小化 ( f(h) ) 就是寻找一个使 ( g’(1)=0 ) 的 ( h )。
八、Surrogate Loss Function Robustness(代理损失函数的鲁棒性分析)
下面比较不同损失函数下 ( g’(1) ) 的形式。
(1) Least squares loss
ℓ(X,Y,h)=(Y−h(X))2
\ell(X,Y,h) = (Y - h(X))^2
ℓ(X,Y,h)=(Y−h(X))2
g′(1)=1n∑i=1n2(yi−h(xi))(−h(xi))
g'(1) = \frac{1}{n}\sum_{i=1}^n 2(y_i - h(x_i))(-h(x_i))
g′(1)=n1i=1∑n2(yi−h(xi))(−h(xi))
(2) Absolute loss
ℓ(X,Y,h)=∣Y−h(X)∣
\ell(X,Y,h) = |Y - h(X)|
ℓ(X,Y,h)=∣Y−h(X)∣
g′(1)=−1n∑i=1n1∣yi−h(xi)∣(yi−h(xi))(−h(xi))
g'(1) = -\frac{1}{n}\sum_{i=1}^n \frac{1}{|y_i - h(x_i)|}(y_i - h(x_i))(-h(x_i))
g′(1)=−n1i=1∑n∣yi−h(xi)∣1(yi−h(xi))(−h(xi))
(3) Cauchy loss
ℓ(X,Y,h)=ln(1+(Y−h(X))2γ2)
\ell(X,Y,h) = \ln\left(1 + \frac{(Y - h(X))^2}{\gamma^2}\right)
ℓ(X,Y,h)=ln(1+γ2(Y−h(X))2)
g′(1)=1n∑i=1n2γ2+(yi−h(xi))2(yi−h(xi))(−h(xi))
g'(1) = \frac{1}{n}\sum_{i=1}^n \frac{2}{\gamma^2 + (y_i - h(x_i))^2}(y_i - h(x_i))(-h(x_i))
g′(1)=n1i=1∑nγ2+(yi−h(xi))22(yi−h(xi))(−h(xi))
(4) Correntropy (Welsch) loss
ℓ(X,Y,h)=1−exp(−(Y−h(X))2σ2)
\ell(X,Y,h) = 1 - \exp\left(-\frac{(Y - h(X))^2}{\sigma^2}\right)
ℓ(X,Y,h)=1−exp(−σ2(Y−h(X))2)
g′(1)=1n∑i=1n2σ2exp(−(yi−h(xi))2σ2)(yi−h(xi))(−h(xi))
g'(1) = \frac{1}{n}\sum_{i=1}^n \frac{2}{\sigma^2}\exp\left(-\frac{(y_i - h(x_i))^2}{\sigma^2}\right)(y_i - h(x_i))(-h(x_i))
g′(1)=n1i=1∑nσ22exp(−σ2(yi−h(xi))2)(yi−h(xi))(−h(xi))
可以发现:
所有损失的导数都包含一个“核心项”:
ci=(yi−h(xi))(−h(xi))
c_i = (y_i - h(x_i))(-h(x_i))
ci=(yi−h(xi))(−h(xi))
而不同的损失函数,对这个项乘了不同的“权重”因子。
- Least squares: 权重 = 常数 2
- Absolute loss: 权重 = (1/∣yi−h(xi)∣)(1/|y_i - h(x_i)|)(1/∣yi−h(xi)∣)
- Cauchy loss: 权重 = (2/[γ2+(yi−h(xi))2])(2 / [\gamma^2 + (y_i - h(x_i))^2])(2/[γ2+(yi−h(xi))2])
- Correntropy loss: 权重 = (2/σ2⋅exp((yi−h(xi))2))(2/\sigma^2 \cdot \exp((y_i - h(x_i))^2 ))(2/σ2⋅exp((yi−h(xi))2))
九、鲁棒性的核心直觉
不同的损失函数对“误差项” (∣yi−h(xi)∣)( |y_i - h(x_i)| )(∣yi−h(xi)∣) 的放大方式不同。
- 对于 Least squares,误差越大,梯度越大 → 对异常值极敏感。
- 对于 Absolute loss,梯度固定方向但幅度有限 → 更稳健。
- 对于 Cauchy loss 与 Correntropy loss,随着误差增大,权重迅速减小 → 异常点几乎被忽略。
因此:
一个损失函数越鲁棒,它在误差增大时分配的梯度权重就越小。
十、实际应用:NMF 的鲁棒性研究
非负矩阵分解(Non-negative Matrix Factorisation, NMF)通常最小化平方误差:
minD,R≥0∣X−DR∣F2
\min_{D,R \ge 0} |X - DR|_F^2
D,R≥0min∣X−DR∣F2
为了增强鲁棒性,可以替换平方损失为更稳健的代理损失:
minD,R≥0∑i=1nℓ(X:,i−DR:,i)
\min_{D,R \ge 0} \sum_{i=1}^n \ell(X_{:,i} - DR_{:,i})
D,R≥0mini=1∑nℓ(X:,i−DR:,i)
例如使用 L1 Loss 或 Cauchy Loss,能抵御异常样本的干扰。
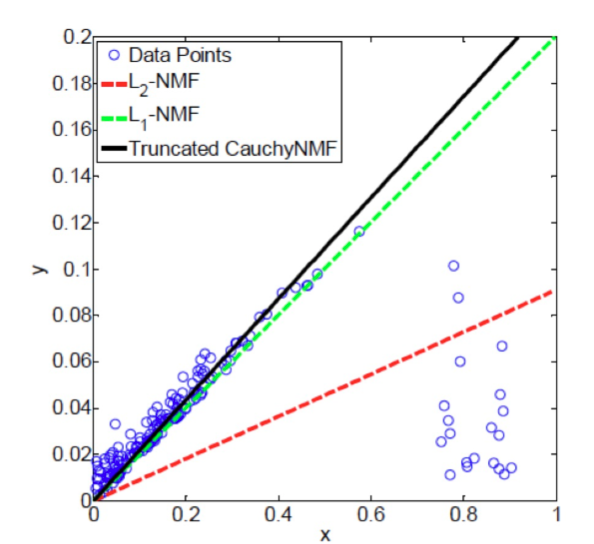
从图像结果可见:
- L2-NMF(红)被异常点严重拉偏;
- L1-NMF(绿)更稳健;
- Truncated Cauchy NMF(黑)几乎不受异常值影响。
最后思考
对于一个给定任务,如果你不确定数据质量(例如有噪声、含异常点),
你应选择一个鲁棒的代理损失函数,如 L1 Loss、Cauchy Loss 或 Correntropy Loss,
而不是传统的平方损失。
总结一句话:
“鲁棒损失的本质是让异常点的梯度贡献变小,从而让模型专注于大多数正常样本。”
