面试150——二叉树

101. 对称二叉树

思路
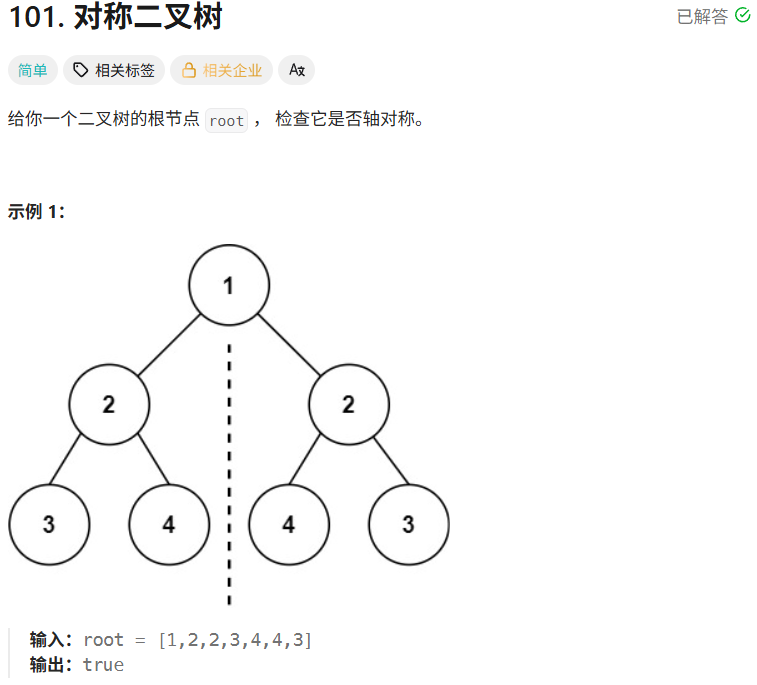
对称二叉树，需要对比一棵树的左分支和右分支是否相等。每一层都需要对称，因此进行层序遍历。通过递归可以实现层序的对比。
代码

class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) return true;return check(root.left, root.right);}public boolean check(TreeNode left, TreeNode right) {if (left == null && right == null) return true;if (left == null || right == null) return false;return left.val == right.val && check(left.left, right.right) && check(left.right, right.left);}
}

114. 二叉树展开为链表

思路
按照先序遍历将二叉树展开成链表。后序遍历，将左子树和右子树都全部先展开成链表并返回链表的尾节点。之后再拼接。
代码

class Solution {public void flatten(TreeNode root) {if (root == null) return;backTraversal(root);}TreeNode backTraversal(TreeNode node) {TreeNode left = node.left, right = node.right;if (left == null && right == null) return node;if (left == null) {return backTraversal(right);}if (right == null) {node.left = null;node.right = left;return backTraversal(left);}TreeNode l = backTraversal(left), r = backTraversal(right);node.left = null;node.right = left;l.right = right;return r;}
}

124. 二叉树中的最大路径和

思路
后序遍历，每次记录左子树和右子树的最大路径，即可求出以当前节点作为根的最大路径和，同时返回最大的一条路径。
代码

class Solution {int res;public int maxPathSum(TreeNode root) {res = -1000010;dfs(root);return res;}int dfs(TreeNode node) {if (node == null) return 0;int l = dfs(node.left);int r = dfs(node.right);res = Math.max(node.val + (l > 0 ? l : 0) + (r > 0 ? r : 0), res);return node.val + Math.max(Math.max(l, r), 0);}
}

222. 完全二叉树的节点个数

思路
满二叉树的计算方式是：假设高度为h，则满二叉树的节点为2^h - 1.对于完全二叉树，其子树一定也是完全二叉树，并且其中有一边一定是满二叉树。因此先序遍历，处理满二叉树情况，如果不是满二叉树则递归计算子树。
代码

class Solution {public int countNodes(TreeNode root) {if (root == null) return 0;TreeNode l = root, r = root;int lh = 0, rh = 0;while (l != null) {lh ++;l = l.left;}while (r != null) {rh ++;r = r.right;}if (lh == rh) return (1 << lh) - 1;return 1 + countNodes(root.left) + countNodes(root.right); }
}

236. 二叉树的最近公共祖先

思路
从下往上一层一层传递信息，使用后序遍历。如果遍历到p或者q则直接返回，如果遍历到底也没有找到p或q则逐层返回null。对于当前遍历的的节点既不是p也不是q，则搜索左子树和右子树。如果左子树和右子树都返回有数则这个就是最近祖先，否则返回那个不为空的部分（当然也可能为空）。
代码

// 后序遍历,如果找到祖先则递归返回最早找到的祖先
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == null || root == p || root == q) return root;TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if (left != null && right != null) return root;return left != null ? left : right;}
}