【剑斩OFFER】算法的暴力美学——二维前缀和
一、题目描述

二、算法原理

一般来说我们遍历数组来进行求和,但是这种时间复杂度太高了:假设我们查找q次区域内和,最差的情况下我们要遍历完整个数组,所以我们的时间复杂度为:O(q * n * n);
我们使用动态规划的思想来完成这道题目,就是上的图片,至于怎么把原数组变成右边的动态规划的数组一会就讲,还有他的时间复杂度也是一会讲。
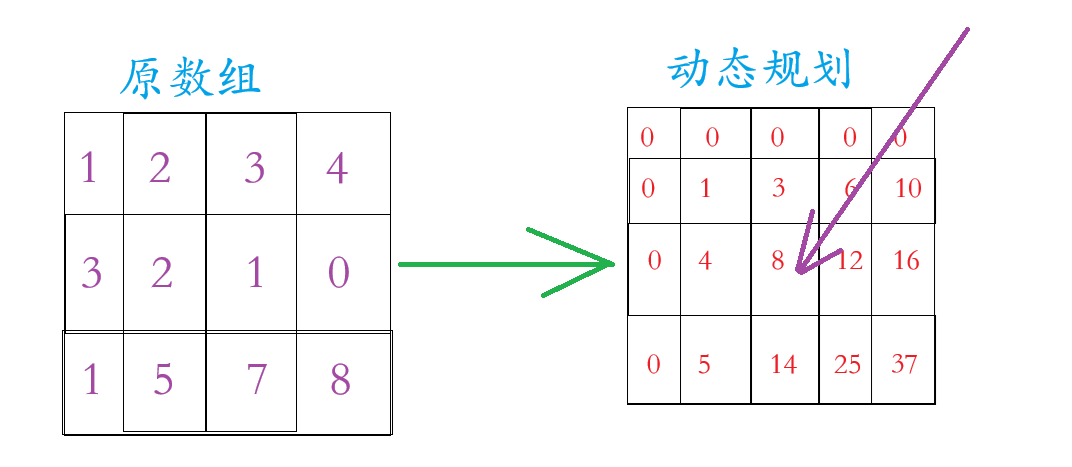
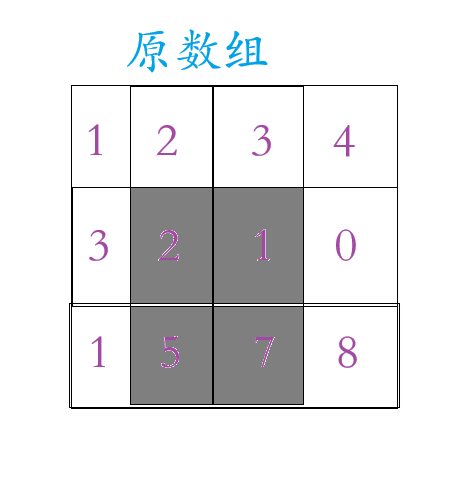
我们看上面的那张图片,动态规划的数组在原数组的基础上多加一行一列(为了边界问题),这一行一列置于0,至于动态规划里面的数字是原数组区域内的和,例如动态规划里面第2行3个数字 =
第1行的 1 + 2,示例:
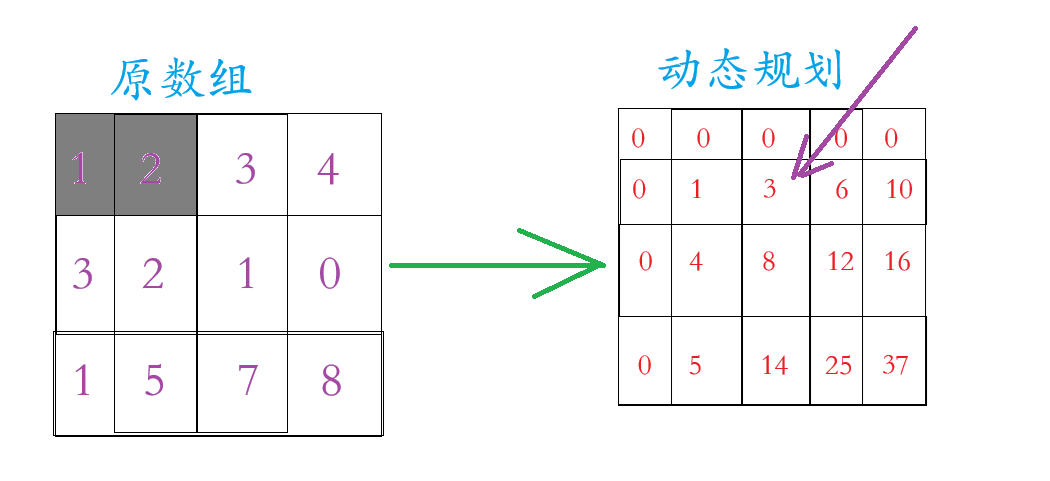
那么动态规划里面:
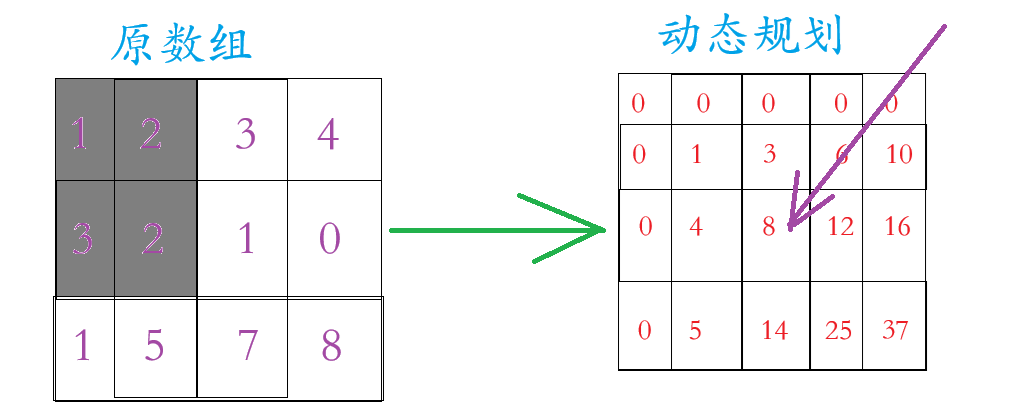
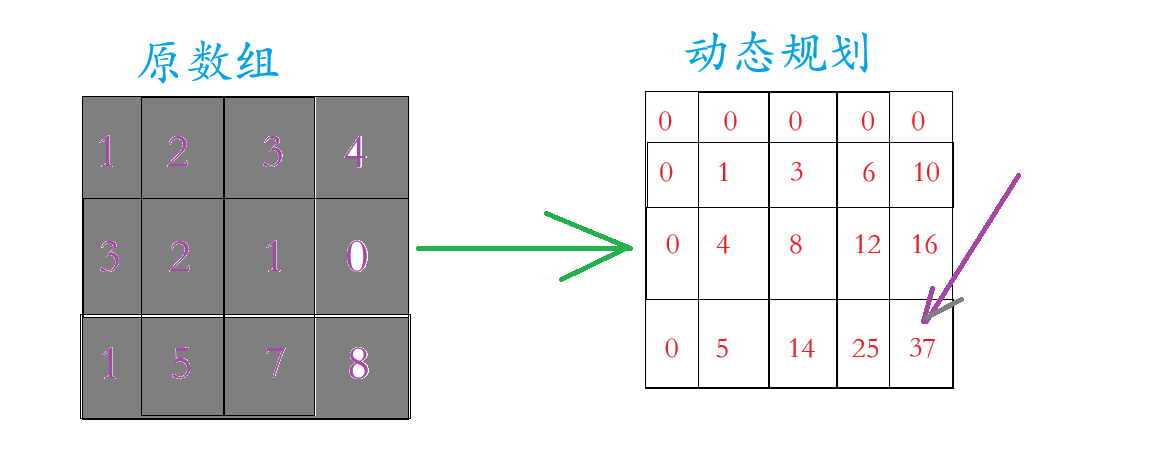
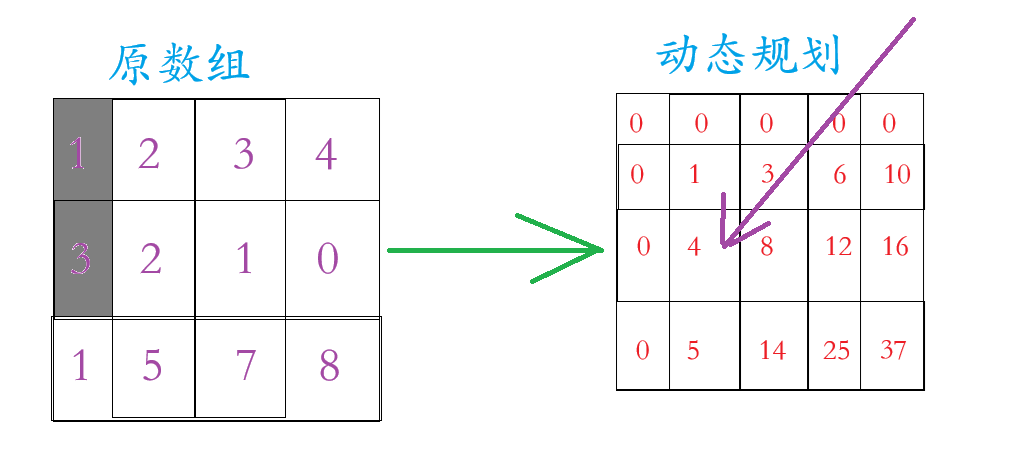
那么怎么把原数组变成动态规划的数组呢?
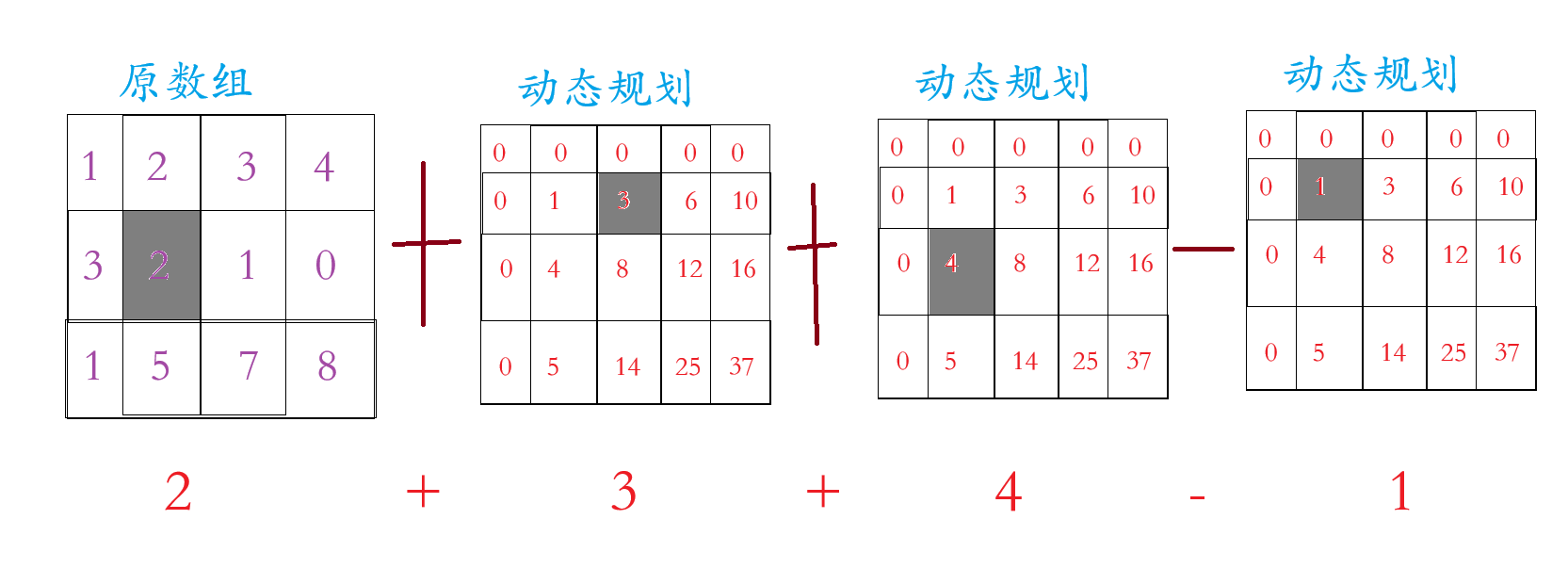
假设我们要求:
等于:
假设我们要求:
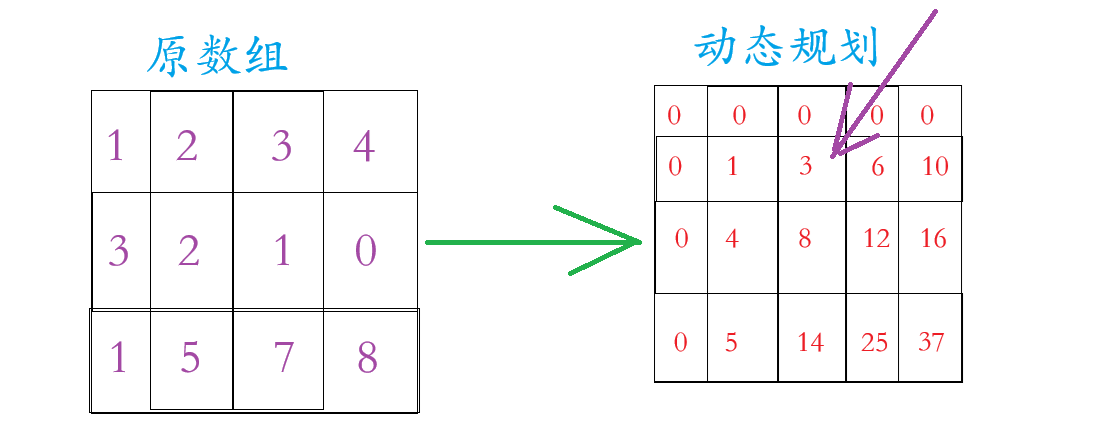
等于:
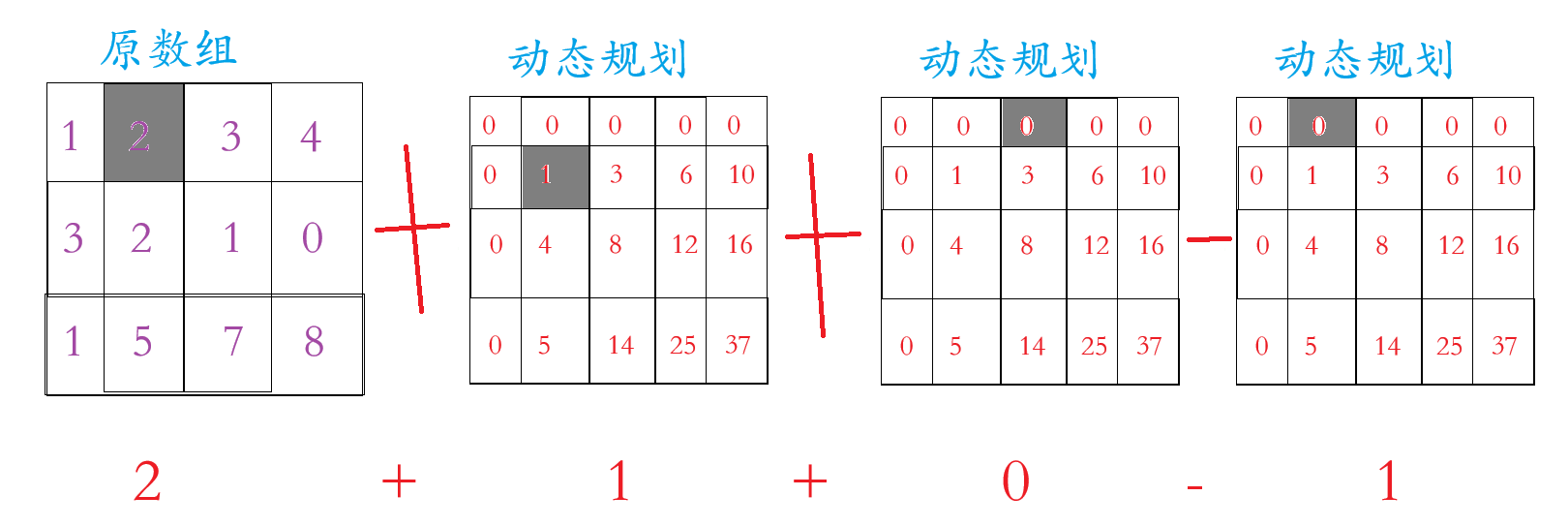
这也是我们为什么要多添加一行一列的原因,不然会越界的,
总结:假设 arr 是原数组,而 new 是动态规划的数组:
假设我们要求 new(x,y)= new[ x - 1][ y ] + new[ x ][ y - 1] - new[ x - 1 ][ y - 1] + arr[ x ][ y ]
那么问题来了,为什么要搞个动态规划的数组出来呢?
先别着急,我们来看一下这个动态规划的数组怎么使用?
假设我们要求原数组这个区域的和:
等于:
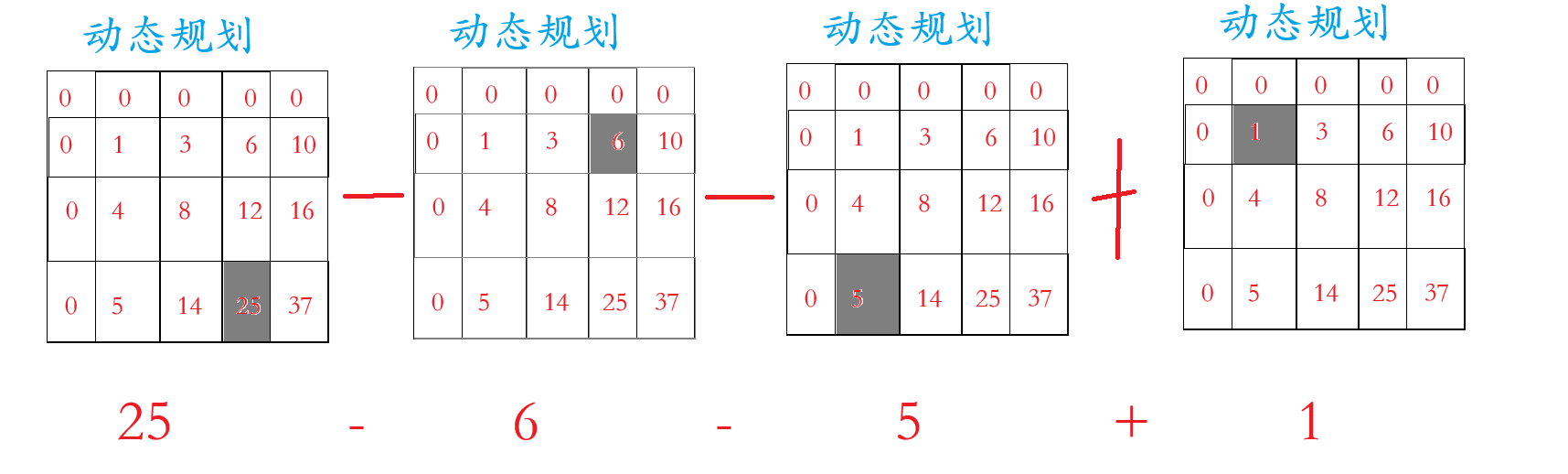
总结:arr(x1 ,y1)—— arr(x2,y2)= new[ x2 ][ y2 ] - new[ x2 ][ y1 - 1 ] - new[ x1 - 1 ][ y2] + new[ x1 - 1][ y1 - 1]
时间复杂度:假设我们要查找 q 次区域内的和:O(1 * q),这就我们为什么要弄个动态规划的数组出来的原因。
三、代码实现
#include <iostream>
#include <vector>
using namespace std;int main()
{long long h = 0,num = 0,index = 0;//h:行数,num:每行的数字的个数,index搜索个数cin >> h >> num >> index;vector<vector<long long>> vv(h + 1,vector<long long>(num + 1));for(long long i = 1; i <= h; i++){for(long long j = 1;j <= num;j++){long long tmp;cin >> tmp;vv[i][j] = vv[i - 1][j] + vv[i][j - 1] - vv[i - 1][j - 1] + tmp;}}for(int i = 0; i < index;i++){long long x1,y1,x2,y2;cin >> x1 >> y1 >> x2 >> y2;cout << vv[x2][y2] - vv[x2][y1 - 1] - vv[x1 - 1][y2] + vv[x1 - 1][y1 - 1] << endl;}return 0;
}
