【PRML】支持向量机

【1】【数之道】支持向量机SVM是什么，八分钟直觉理解其本质
【2】

1-基本概念

1.1-问题建模

如何设计$M-1$维度的超平面把两类维度是$M$的样本点分开
两个概念

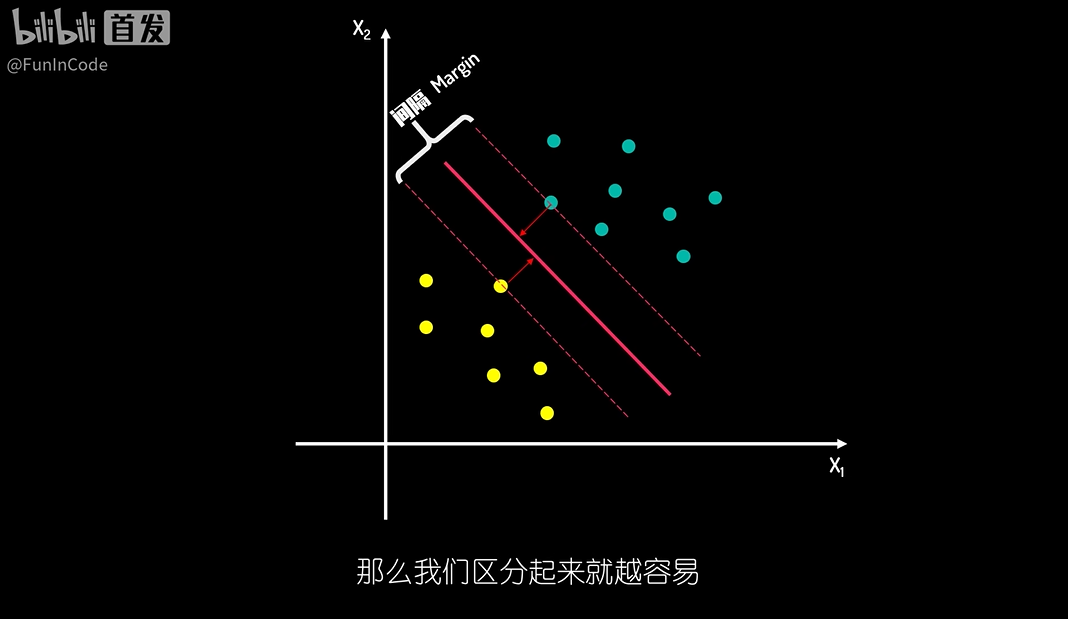
• 间隔 margin：越大的间隔，则两类数据差异越大，越容易区分（the smallest distance between the decision boundary and any of the samples）
• 决策边界 decision boundary : 求解最佳决策边界的问题可以转化为求解两类数据的最大间隔问题，而间隔的中间就是决策边界 （In support vector machines the decision boundary is chosen to be the one for which the margin is maximized.）
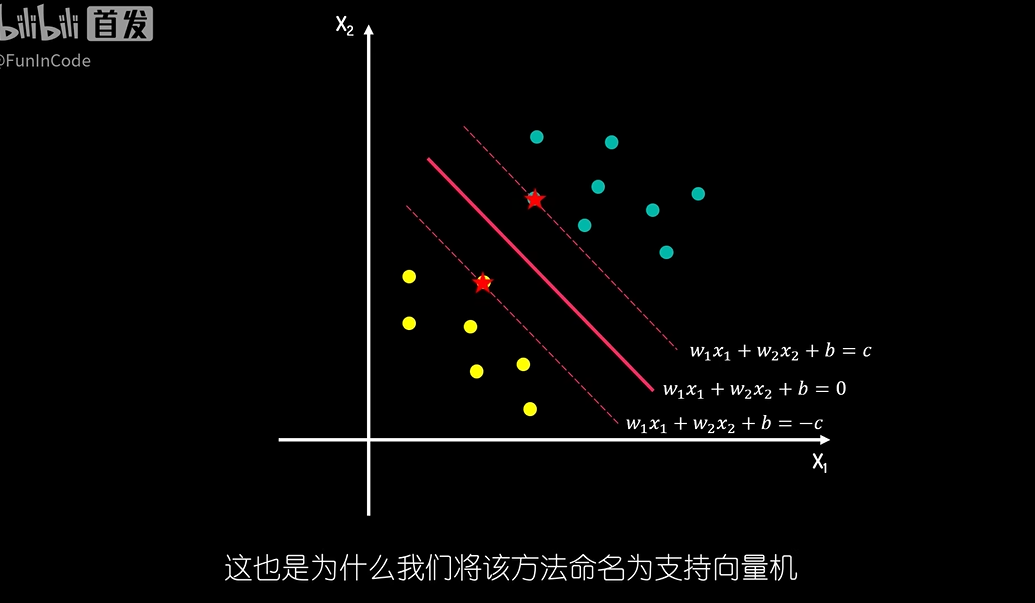
• 支持向量 support vectors ：离决策边界最近的两类样本的数据 The location of this boundary is determined by a subset of the data points, known as support vectors,

1.2-数学建模

三个线性方程

决策边界
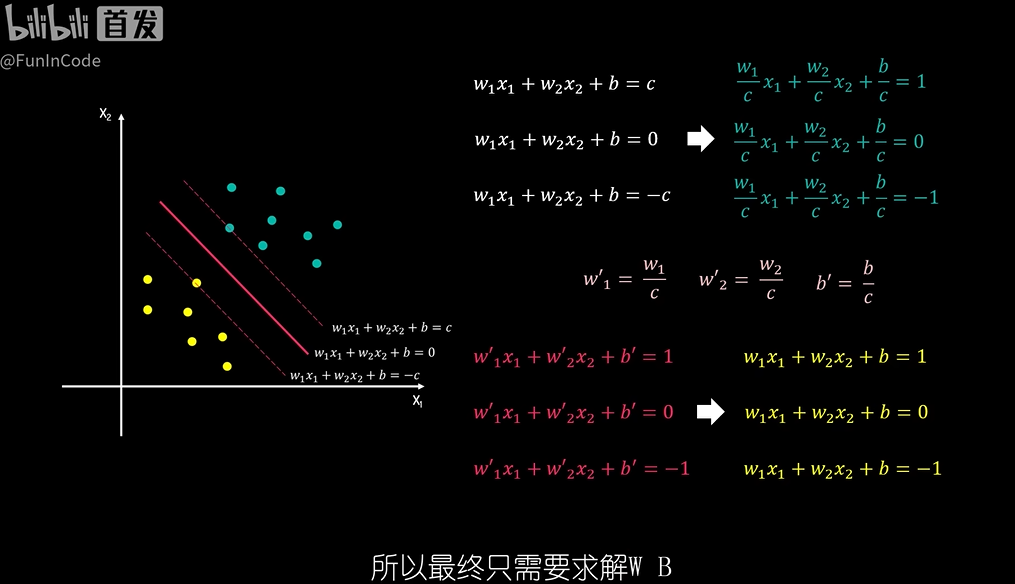
决策边界上下移动$c$得到间隔上下边界

三个方程等式两边同时除以$c$，并变量代换，得到新的三个方程

正负超平面与决策超平面，如何对$w$与$b$求解

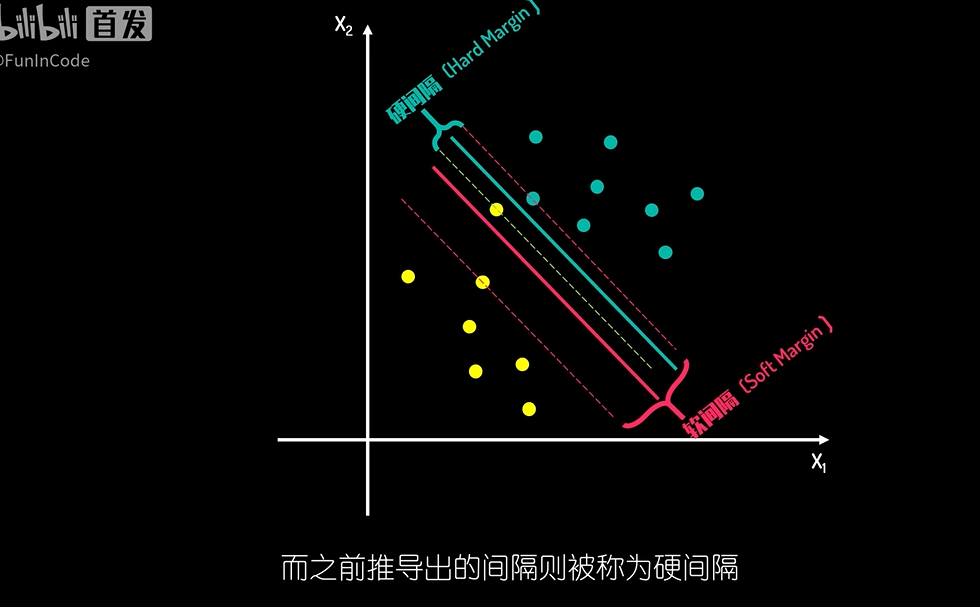
软间隔与硬间隔 （soft margin）

• 是否需要为了一个异常值，牺牲间隔距离？
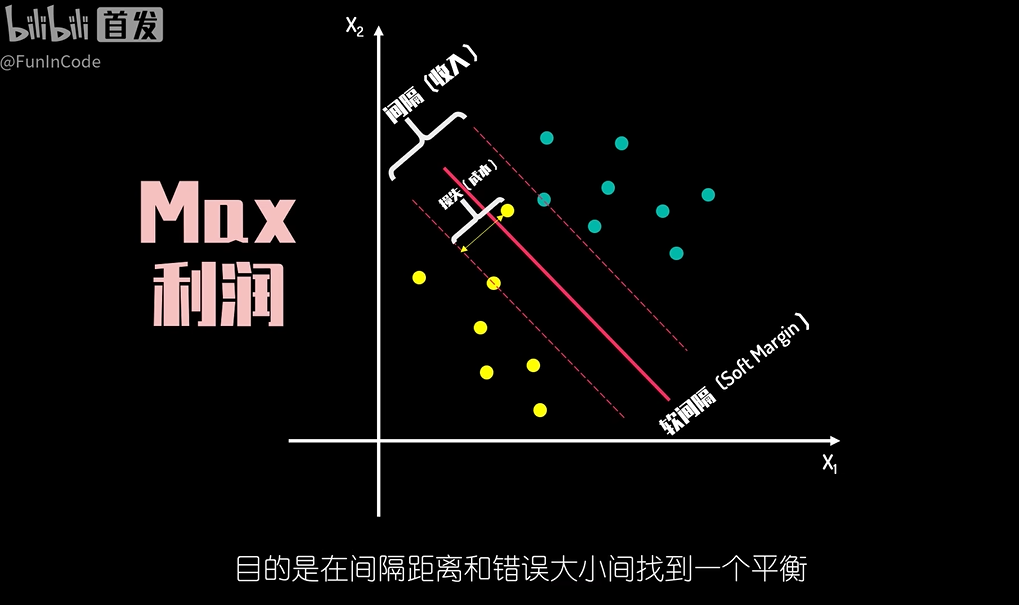
• 当有更多的异常值？引入损失因子的概念（成本），间隔是收入，最大化利润，这个最优解下形成的间隔称之为软间隔
• soft margin 允许一定容错率，本质是在间隔距离大小和错误大小之间找一个平衡

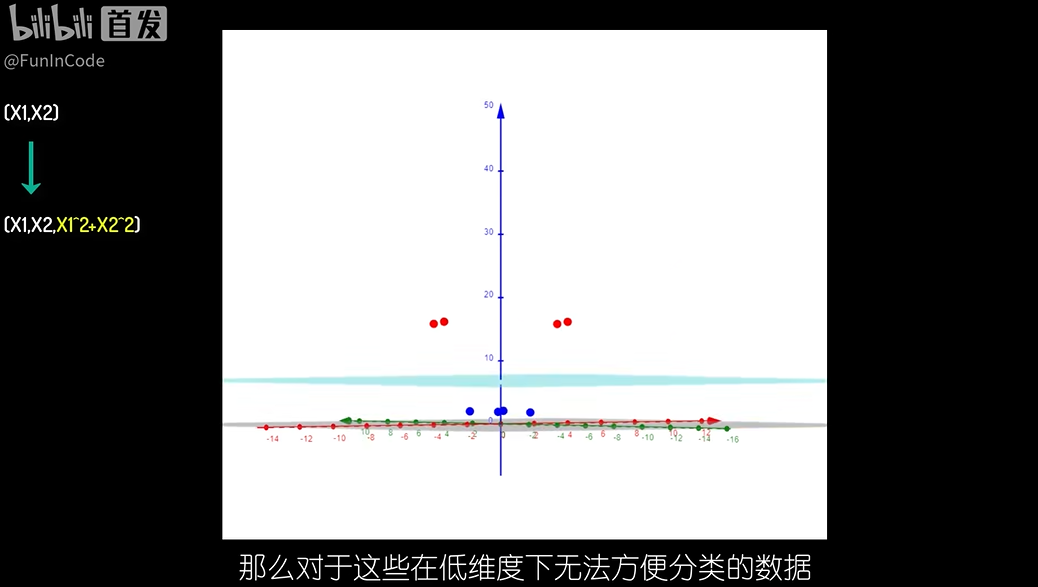
维度转换使得原本不能区分的数据能区分

• 先对低维数据升维
• 然后在高纬度下利用SVM，利用高纬度下的决策超平面分类
• 利用维度转换函数提升维度？这需要更多的数据存储与计算需求，有没有一种方法能避免将数据送入高维度进行计算

核技巧（kernel trick）：提供高纬度向量相似度的测量（其实SVM本来也就是用来衡量两类数据之间的差异）

• 选取合适的核公式，即使没有具体的维度转换函数，也可以直接获取数据的高维度差异度

2-数学求解

2.1-问题建模

求解决策超平面

• 找超平面目标是最大化间隔，先把间隔数学表达$L$
• 先分别在正负超平面上选取一个支持向量点，这两个点满足各自的超平面方程 1 和 2
• 转化为两个向量的点积

在决策超平面随机取两个点

• 类似地转化为点积
• 发现向量