磁共振成像原理（理论）36：回波平面成像 (Echo-Planar Imaging)

本专题主要参考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 9.3

回波平面成像

回波平面成像（Echo-Planar Imaging, EPI）是曼斯菲尔德于1977年提出的首种超高速成像技术。此后发展出多种变体。如今该术语广泛指代在单次激发脉冲后的自由感应衰减期内采集"完整"二维编码集的高速成像方法类别。因此，EPI已成为单次激造成像的同义词，尽管具有交错k空间覆盖的多激发EPI方法也常用。

EPI的关键概念是利用时变梯度遍历k空间。接下来讨论三种流行的k空间轨迹：Z字形轨迹、直线轨迹和螺旋轨迹。

Z字形轨迹

为理解单次激发下的k空间覆盖，首先考虑曼斯菲尔德提出的原始EPI方法（图9.8）。该成像方案在读出期间使用一对频率编码梯度：小型恒定梯度和快速交变梯度。交变梯度在自由进动期间产生一系列梯度回波，从而实现快速成像。

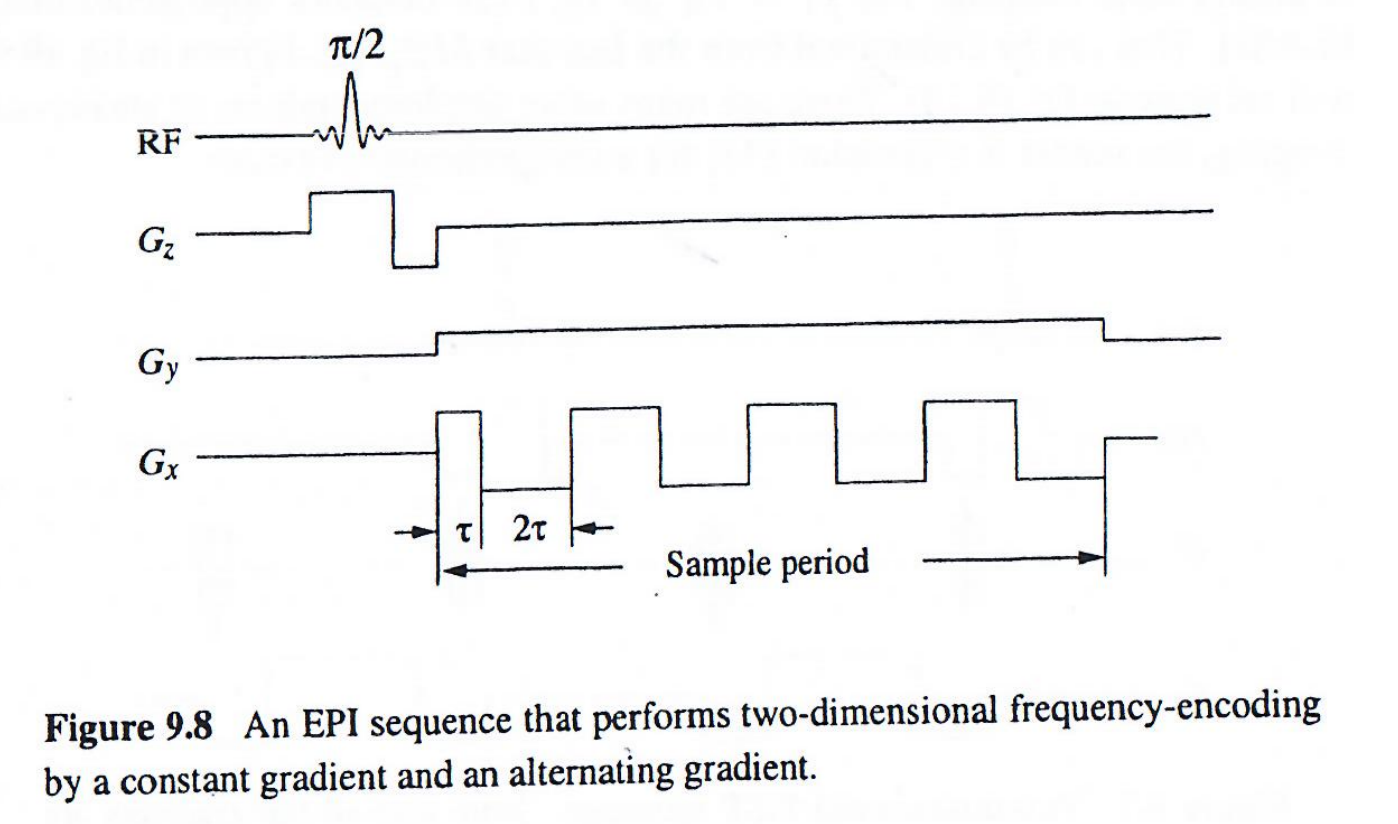
根据k空间定义：
$$k(t)=\gamma {\int }_0^{t}G(\tau )d\tau \text{\hspace{1em}(9.43)}$$

上图9.8所展示的序列对应的k空间编码为：
$$k_y(t)=\gamma G_{y}t\text{\hspace{1em}(9.44a)}$$
$$k_x(t)=\{\begin{array}{ll}\gamma G_{x}t,& 0<t<\tau \\ \gamma G_x(2\tau -t),& \tau <t<3\tau \\ \gamma G_x(t-4\tau ),& 3\tau <t<5\tau \end{array}\text{\hspace{1em}(9.44b)}$$

因此，该序列产生的每个梯度回波被映射到倾斜的k空间线，形成下图9.9所示的Z字形轨迹。注意该轨迹仅覆盖k空间上半部分。为获得全k空间覆盖，需形成自旋回波或梯度回波。

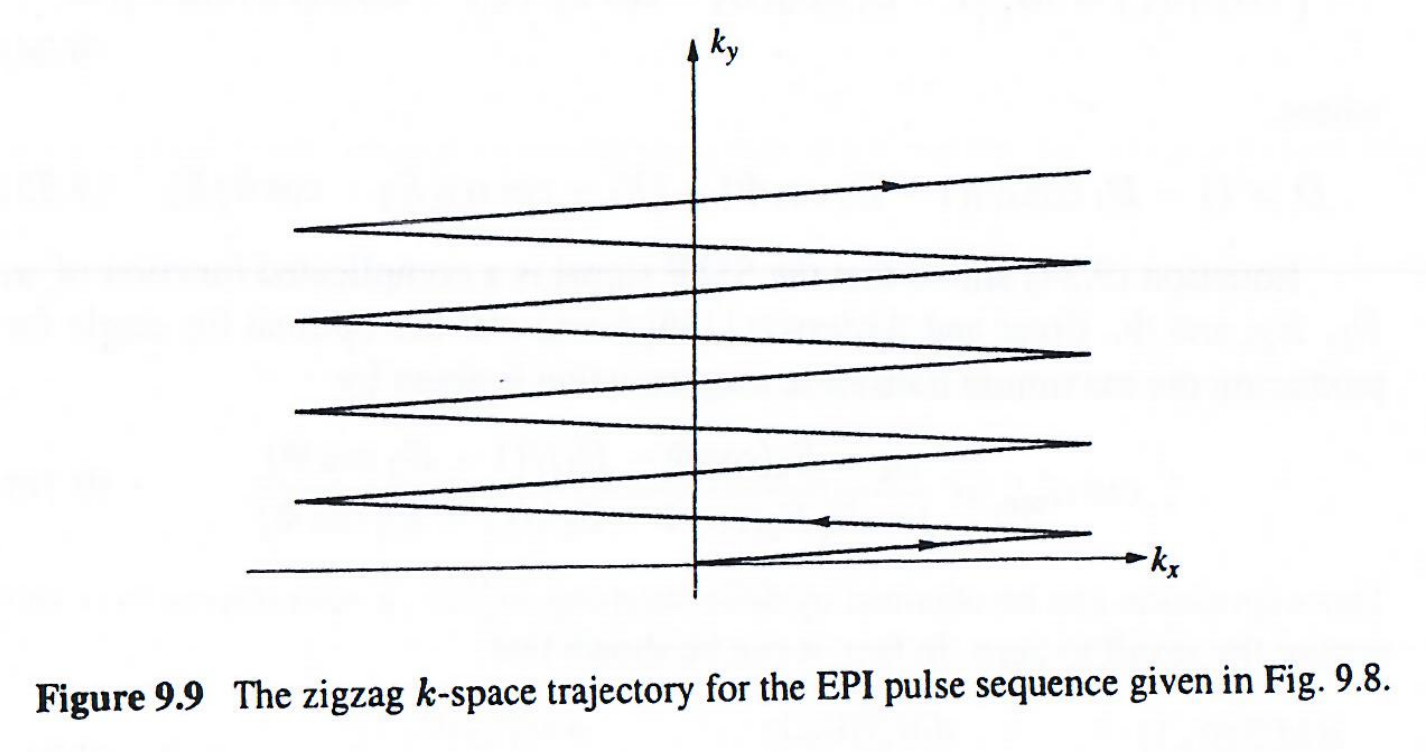
Z字形轨迹的实际问题是需要特殊图像重建算法，因为沿$k_y$方向的采样是非均匀的。解决方法之一是使用交错采样理论。具体而言，固定$k_x$值时，沿$k_y$轴的信号变化可表示为$S(k_y)$，其采样如图9.10所示。

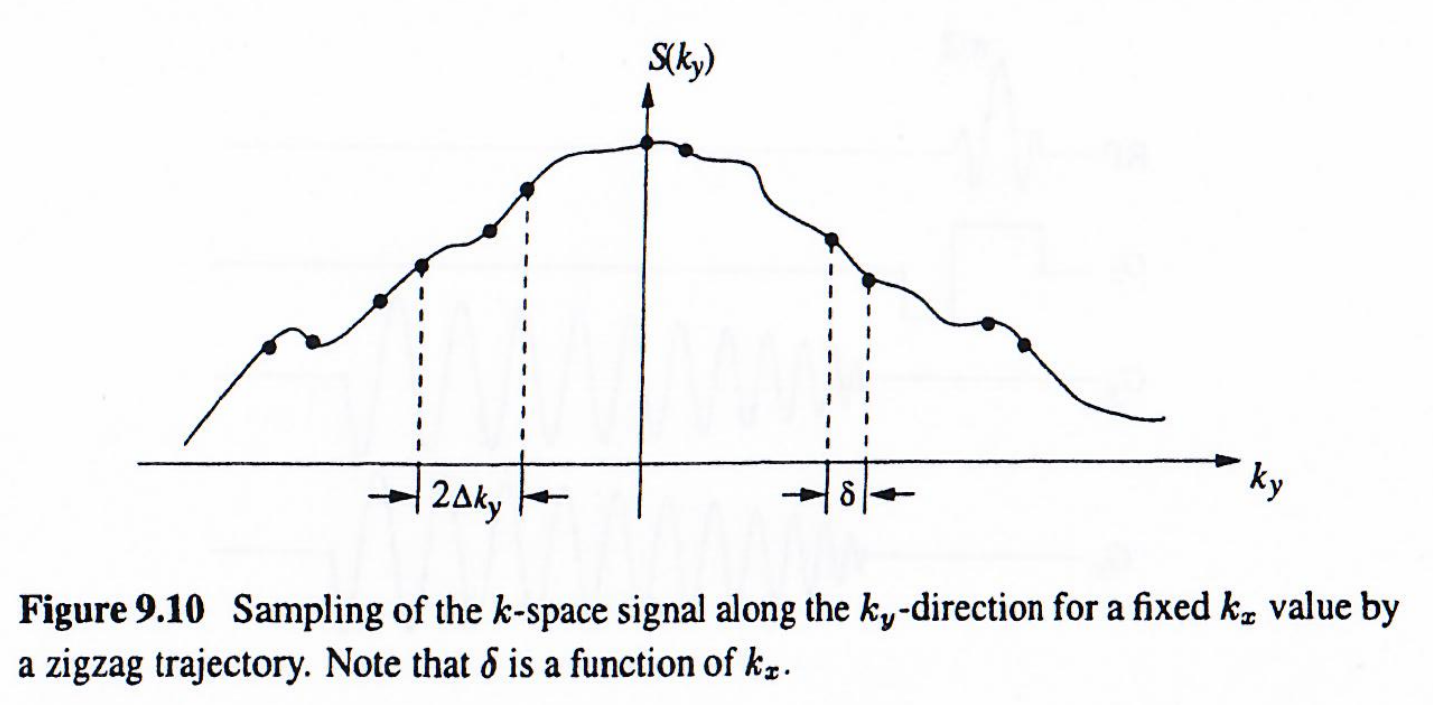
将采样点分为奇偶索引序列：
$$S_o[n]=S(2n\Delta k_y)\text{\hspace{1em}(9.45)}$$
$$S_e[n]=S(2n\Delta k_y+\delta )\text{\hspace{1em}(9.46)}$$

在理想无限采样下，回忆式子(6.10)如下
$$\sum _{n=-\infty }^{\infty }S[n]e^{i2\pi n\Delta kx}=\frac{1}{\Delta k}\sum _{n=-\infty }^{\infty }I\left(x-\frac{n}{\Delta k}\right)\text{\hspace{1em}(6.10)}$$
$$\hat{I}(x)=\sum _{n=-\infty }^{\infty }I\left(x-\frac{n}{\Delta k}\right)=\Delta k\cdot \sum _{n=-\infty }^{\infty }S[n]e^{i2\pi n\Delta kx}\text{\hspace{1em}(6.10-new)}$$
根据式子(6.10)，将$x\to y$，奇索引的傅里叶重建结果为：
$$I_o(y)=\sum _{n}I\left(y-\frac{n}{2\Delta k_y}\right)\text{\hspace{1em}(9.47)}$$
偶索引的傅里叶重建结果为：
$$I_e(y)=\sum _n{e}^{in\pi \delta }I\left(y-\frac{n}{2\Delta k_y}\right)\text{\hspace{1em}(9.48)}$$

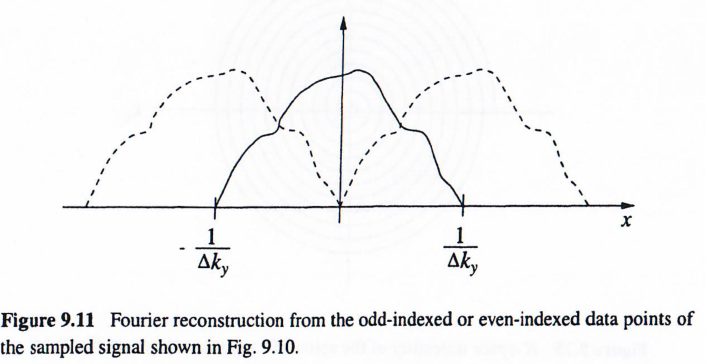
当$\Delta k_y$取奈奎斯特采样间隔时，$I_o(y)$和$I_e(y)$会产生混叠伪影（图9.11）。但在特定区间内可通过代数运算消除：

对于$0\le y\le 1/(2\Delta k_y)$区间：
$$I_o(y)=I(y)+I\left(y-\frac{1}{2\Delta k_y}\right)\text{\hspace{1em}(9.49a)}$$
$$I_e(y)=I(y)+e^{i\pi \delta }I\left(y-\frac{1}{2\Delta k_y}\right)\text{\hspace{1em}(9.49b)}$$

对于$-1/(2\Delta k_y)\le y\le 0$区间：
$$I_o(y)=I(y)+I\left(y+\frac{1}{2\Delta k_y}\right)\text{\hspace{1em}(9.50a)}$$
$$I_e(y)=I(y)+e^{-i\pi \delta }I\left(y+\frac{1}{2\Delta k_y}\right)\text{\hspace{1em}(9.50b)}$$

通过简单代数运算可得解混叠公式：
$$I(y)=\{\begin{array}{ll}\frac{e^{i\pi \delta }}{e^{i\pi \delta }-1}{I}_o(y)+\frac{1}{e^{i\pi \delta }-1}{I}_e(y),& 0\le y\le 1/(2\Delta k_y)\\ \frac{e^{-i\pi \delta }}{e^{-i\pi \delta }-1}{I}_o(y)+\frac{1}{e^{-i\pi \delta }-1}{I}_e(y),& -1/(2\Delta k_y)\le y\le 0\end{array}\text{\hspace{1em}(9.51)}$$

实际有限采样时，$I_o(y)$和$I_e(y)$可用常规FFT算法重建，再按式子(9.51)重组得到$I(y)$。

直线轨迹

Pykett和Rzedzian（1987）提出的EPI序列可实现k空间正交采样（图9.12）。该序列使用系列blipped $G_y$脉冲对单个梯度回波进行相位编码。与传统成像不同，此处相位编码梯度幅度恒定，无需递增步进，因为横向磁化会累积每个相位编码blip引入的相位分散。这种相位累积效应在传统成像中不会发生，因为每个相位编码步会生成新的横向磁化。

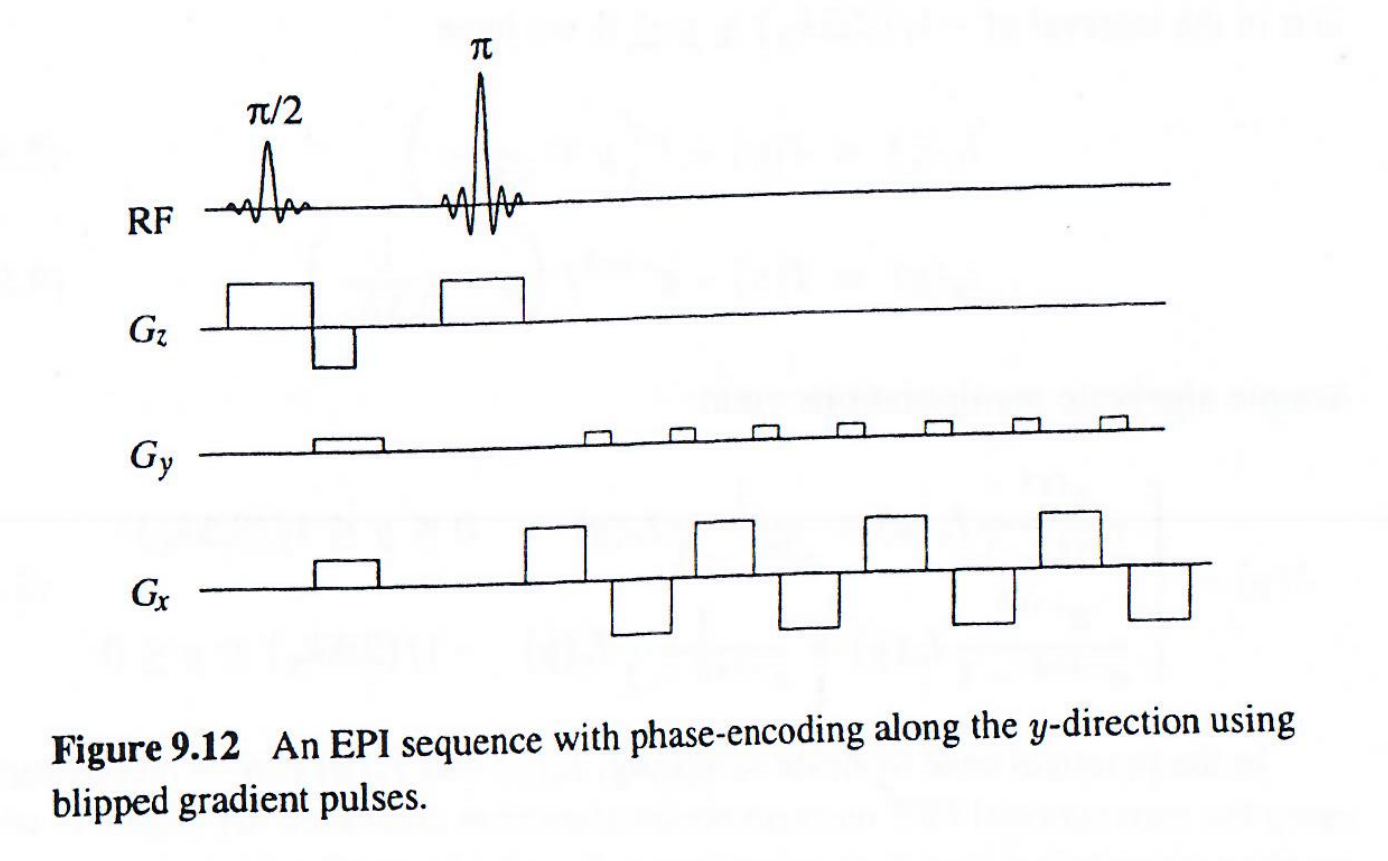
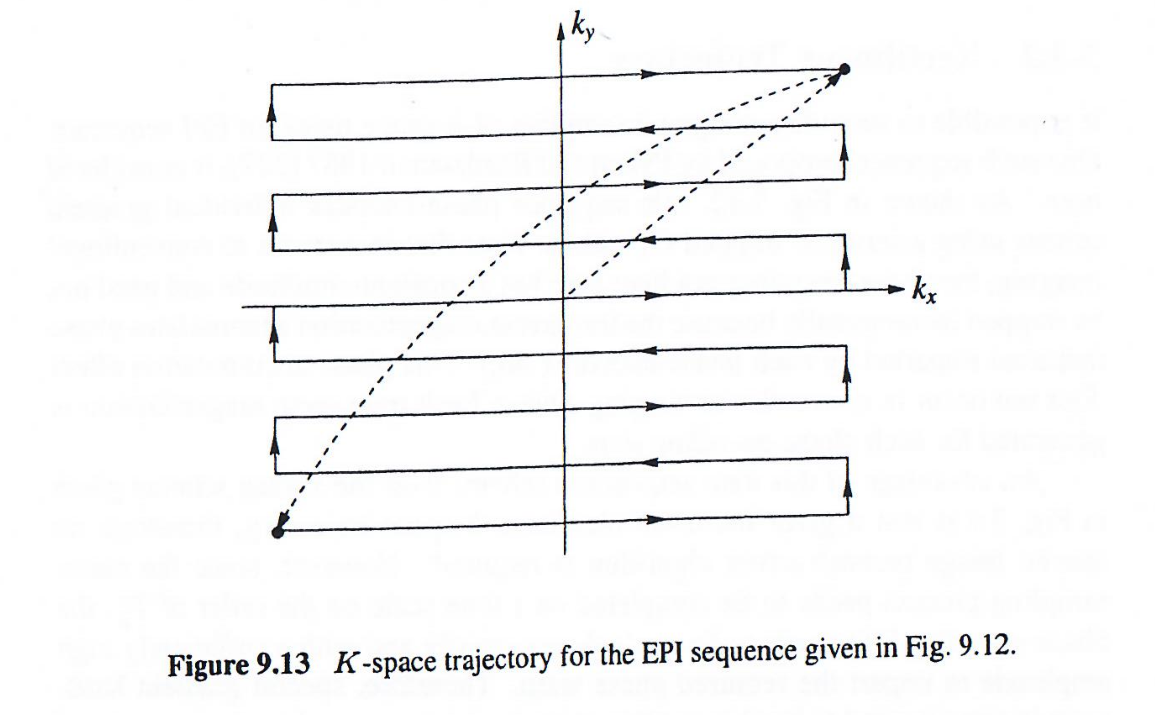
该方案相比Z字形轨迹的优势是产生常规直线k空间轨迹（图9.13），无需特殊重建算法。但由于整个采样过程需在T2时间尺度内完成，相位编码blip需快速施加且幅度足够高，因此常需特殊梯度硬件（要求快速切换，需要梯度电流带宽要求较高）实现。

螺旋轨迹

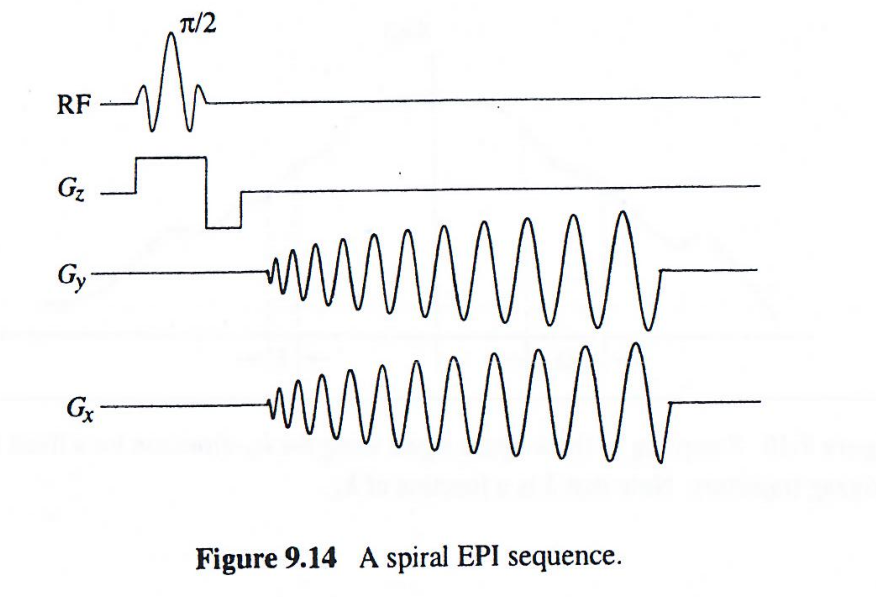
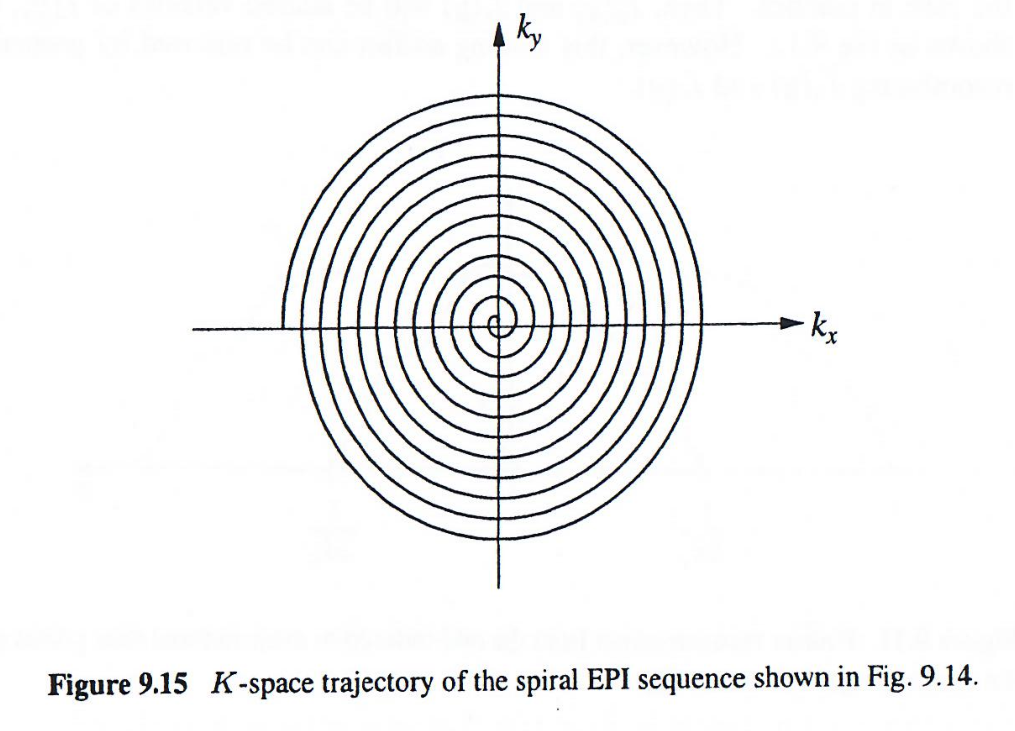
图9.14所示的单次成像方法对梯度硬件要求较低。该方法使用一对递增正弦梯度以螺旋方式遍历k空间（图9.15），称为螺旋成像。该方法完全消除了先前序列所需的快速梯度切换。

螺旋轨迹的数学表达式为：

$$\mathbf{k}(t)=A\omega (t)e^{i\omega (t)}\text{\hspace{1em}(9.52)}$$

其中$k=k_x+i{k}_y$，$\omega (t)$和$\phi (t)$是时间函数。螺旋序列设计的关键步骤是角速度函数选择。例如：
$$\omega (t)={\omega }_{0}t\text{\hspace{1em}(9.53)}$$

对应k空间轨迹为：
$$\mathbf{k}(t)=A{\omega }_{0}t{e}^{i{\omega }_{0}t}\text{\hspace{1em}(9.54)}$$

或简化为：
$$\mathbf{k}(t)=At{e}^{i{\omega }_{0}t}\text{\hspace{1em}(9.55)}$$

根据k空间定义：
$$k(t)=\gamma {\int }_0^{t}G(\tau )d\tau \text{\hspace{1em}(9.43)}$$

所需梯度函数为：
$$\begin{array}{rl}\mathbf{G}(t)& =\frac{1}{\gamma }\frac{d}{dt}\mathbf{k}(t)\\ & =A{e}^{i{\omega }_{0}t}+iAt{\omega }_0{e}^{i{\omega }_{0}t}\end{array}\text{\hspace{1em}(9.56)}$$

其中$G(t)\equiv G_x+i{G}_y$。对应梯度通道为：

$$G_x(t)=A\cos {\omega }_{0}t-At{\omega }_0\sin {\omega }_{0}t\text{\hspace{1em}(9.57a)}$$
$$G_y(t)=A\sin {\omega }_{0}t+At{\omega }_0\cos {\omega }_{0}t\text{\hspace{1em}(9.57b)}$$

该梯度对定义的螺旋路径具有恒定角速度（公式9.55所示），意味着k空间中心区域耗时比外围多。实际上，由于梯度强度限制，外围区域的扫描速度可能过大。该问题可通过恒定线速度螺旋轨迹克服，例如设：
$$\omega (t)={\omega }_0\sqrt{t}\text{\hspace{1em}(9.58)}$$

对应地：
$$\mathbf{k}(t)=A\sqrt{t}{e}^{i{\omega }_0\sqrt{t}}\text{\hspace{1em}(9.59)}$$

且：
$$G(t)=\frac{A}{2t}{e}^{i{\omega }_0\sqrt{t}}+\frac{A}{2}{\omega }_0{e}^{i{\omega }_0\sqrt{t}}\text{\hspace{1em}(9.60)}$$

在k空间外围区域（t较大时）：
$$\mathbf{G}(t)\approx \frac{A}{2}{\omega }_0{e}^{i{\omega }_0\sqrt{t}}\text{\hspace{1em}(9.61)}$$

意味着G(t)幅度变为常数。

该梯度函数的问题是在t=0处有极点，实际中因梯度强度和上升时间限制难以实现。更实用的螺旋轨迹定义为：
$$\mathbf{k}(t)=At\sqrt{1+t/T}{e}^{i{\omega }_{0}t\sqrt{1+t/T}}\text{\hspace{1em}(9.62)}$$

其中$T$为时间参数，使$k(t)$在t≪T时具恒定角速度，t≫T时具恒定线速度。

螺旋轨迹数据需要特殊图像重建算法。实践中常用数据插值方案将螺旋数据映射到矩形网格，再用常规傅里叶重建算法处理。使用方形螺旋轨迹可减轻插值问题，仅需一维插值。

讨论

当前梯度技术下，EPI方法可在约50ms内采集二维图像，克服了生理运动引起的图像退化问题。此外，单次EPI的有效$T_R$无限长，产生具真实$T_2$或$T_2^{\ast }$对比度的图像。

尽管有这些优势，EPI方法仍有若干固有局限。首先，最大可达分辨率受$T_2\ast$值限制。具体地，$T_2\ast$点扩散函数（PSF）可写为：
$$h(x)=\frac{\gamma G_x{T}_2^{\ast }}{-1+i\gamma G_x{T}_2^{\ast }x}\text{\hspace{1em}(9.63)}$$

虽然该PSF沿读出方向可忽略，但在其他方向可能导致显著模糊，因为数据采集时间远大于$T_2\ast$。此外，EPI图像可能因偏共振效应和梯度误差产生明显伪影。