【数据结构】并查集（操作详解 + 模板 + 练习）

一、并查集

1. 双亲表示法

在学习树这个数据结构的时，我们直到树的存储方式有很多种：孩子表示法，双亲表示法、孩子双亲表示法以及孩子兄弟表示法等。对一棵树而言，除了根节点外，其余每个结点一定有且仅有一个双亲，双亲表示法就是根据这个特点存储树的，也就是把每个结点的双亲存下来。因此，我们可以采用数组来存储每个结点的父亲结点的编号，这就实现了双亲表示法 so easy。

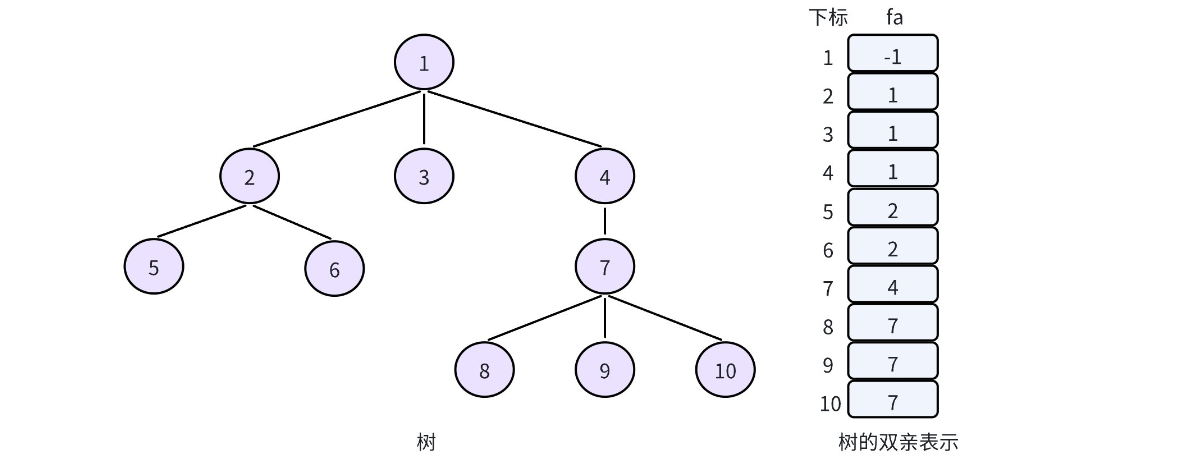
双亲表示法常用来实现并查集，而在实现并查集的时，我们一般让根节点自己指向自己。因此，上述存储就变成：

---

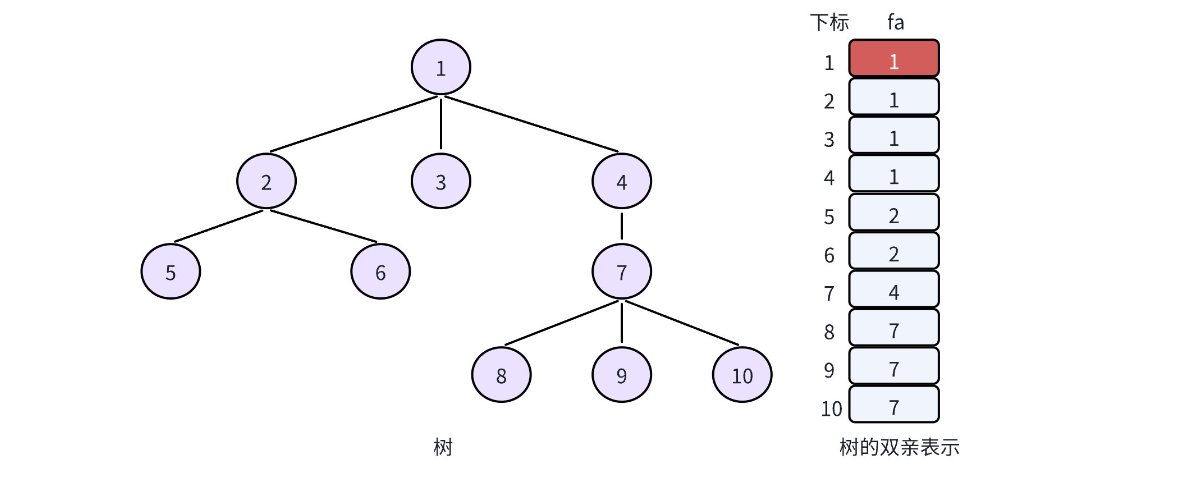
2. 并查集的概念

并查集，本质上就是用双亲表示法实现的森林。

在有些问题中，我们需要维护若干个集合，并且基于这些集合要频繁执行下面的操作：

• 查询操作：查找元素 x 属于哪一个集合。一般会在每个集合中选取一个元素作为代表，查询的是这个集合中的代表元素；

• 合并操作：将元素 x 所在的集合与元素 y 所在的集合合并成一个集合；（注意，合并的是元素所在的集合，不是这两个元素）

• 判断操作：判断元素 x 和 y 是否在同一个集合。

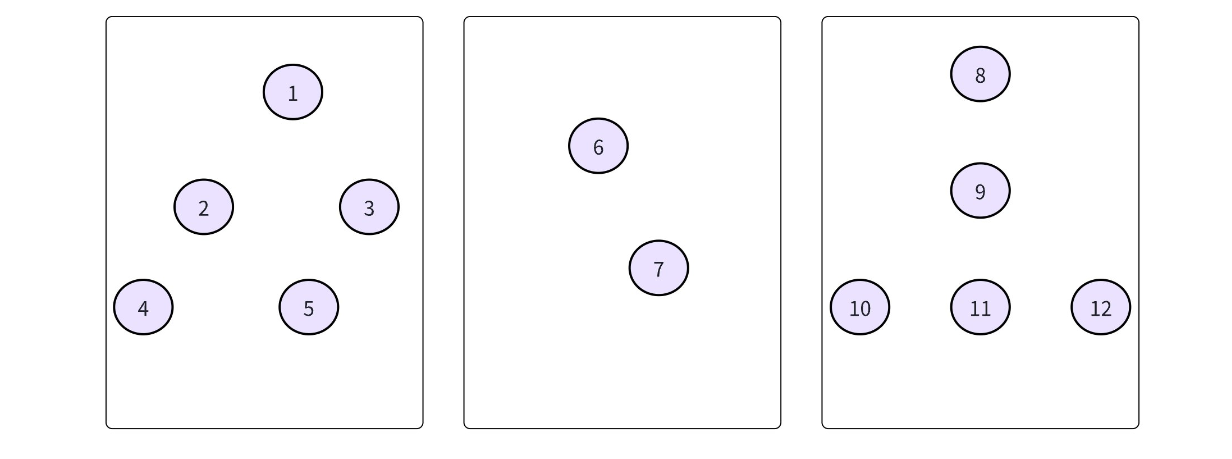
并查集（UnionFindSet）：是一种用于维护元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素，根节点来代表整个集合。上面所说的代表元素实际上指的就是根节点。

---

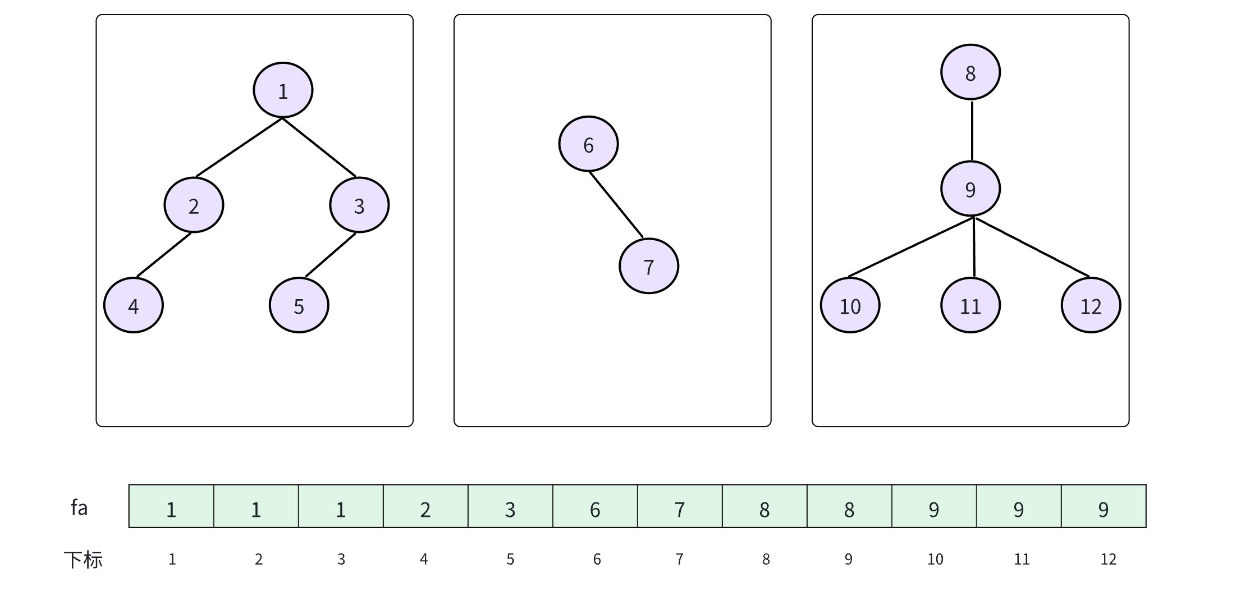
3. 并查集的实现

(1) 初始化

初始状态下，可以看成是所有的元素单独成为一个集合：让元素自己指向自己即可。

const int N = 1e6 + 10;
int pa[N];  // 存储父节点的下标
int n;  // 有 n 个元素void init()
{for(int i = 1; i <= n; i++) pa[i] = i;
}

---

(2) 查询操作

查询操作是并查集的核心操作，其余所有的操作都是基于查询操作实现的！ 找到元素 x 所属的集合，返回所属集合的根节点下标：一直向上找爸爸即可。

int find(int x)
{if(pa[x] == x) return x;  // 如果是根节点, 返回即可return find(pa[x]);  // 如果不是, 则向上找爸爸
}

---

(3) 合并操作

将元素 x 所在的集合与元素 y 所在的集合合并成一个集合：让元素 x 所在树的根节点指向元素 y 所在树的根节点。（反过来也是可以的）

void uni(int x, int y)
{int fx = find(x);int fy = find(y);pa[fx] = fy;
}

---

(4) 判断操作

判断元素 x 和元素 y 是否在同一集合：只需看看两者所在树的根节点是否相同。

bool isSame(int x, int y)
{return find(x) == find(y);
}

---

4. 并查集的优化

在极端情况下，合并的过程中，整棵树会变成一个链表，这样的话查询操作就会变得很慢。于是我们需要进行优化。

路径压缩：在查询时，把被查询的节点到根节点的路径上的所有节点的父节点设置为根节点，从而减小树的深度。也就是说，在向上查询的同时，把在路径上的每个节点都直接连接到根上，以后查询时就能直接查询到根节点。

int find(int x)
{if(pa[x] == x) return x;return pa[x] = find(pa[x]);
}

还有一种优化方式是按秩合并，但是基本上不用按秩合并，并查集的时间复杂度就很优秀了。感兴趣的话可以搜一下按秩合并，在《算法导论》中也有严格的证明，并查集查询根节点的最坏时间复杂度为 $O(\alpha (n))$，是一个很小的常数。因此，并查集查询以及合并的效率近似可以看成 $O(1)$。

---

5. 【模板】并查集 ⭐⭐

【题目链接】

P3367 【模板】并查集 - 洛谷

【题目描述】

如题，现在有一个并查集，你需要完成合并和查询操作。

【输入格式】

第一行包含两个整数 $N,M$ ,表示共有 $N$ 个元素和 $M$ 个操作。

接下来 $M$ 行，每行包含三个整数 $Z_i,X_i,Y_i$ 。

当 $Z_i=1$ 时，将 $X_i$ 与 $Y_i$ 所在的集合合并。

当 $Z_i=2$ 时，输出 $X_i$ 与 $Y_i$ 是否在同一集合内，是的输出
Y ；否则输出 N 。

【输出格式】

对于每一个 $Z_i=2$ 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

【示例一】

输入

4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

输出

N
Y
N
Y

【说明/提示】

对于 $15\%$ 的数据，$N\le 10$，$M\le 20$。

对于 $35\%$ 的数据，$N\le 100$，$M\le 10^3$。

对于 $50\%$ 的数据，$1\le N\le 10^4$，$1\le M\le 2\times 10^5$。

对于 $100\%$ 的数据，$1\le N\le 2\times 10^5$，$1\le M\le 10^6$，$1\le X_i,Y_i\le N$，Zi∈{1,2}Z_i \in \{ 1, 2 \}Zi​∈{1,2}。

---

模板题，利用上面所讲的操作即可。

#include<iostream>using namespace std;const int N = 2e5 + 10;
int pa[N];
int n, m;void init()
{for(int i = 1; i <= n; i++) pa[i] = i;
}int find(int x)
{if(pa[x] == x) return x;return pa[x] = find(pa[x]);
}void uni(int x, int y)
{int fx = find(x);int fy = find(y);pa[fx] = fy;
}bool issame(int x, int y)
{return find(x) == find(y);
}int main()
{cin >> n >> m;init();while(m--){int z, x, y;cin >> z >> x >> y;if(z == 1) uni(x, y);else{bool res = issame(x, y);if(res) cout << 'Y' << endl;else cout << 'N' << endl;}}return 0;
}

---

二、OJ 练习

1. 亲戚 ⭐⭐

【题目链接】

P1551 亲戚 - 洛谷

【题目背景】

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

【题目描述】

规定：$x$ 和 $y$ 是亲戚，$y$ 和 $z$ 是亲戚，那么 $x$ 和 $z$ 也是亲戚。如果 $x$，$y$ 是亲戚，那么 $x$ 的亲戚都是 $y$ 的亲戚，$y$ 的亲戚也都是 $x$ 的亲戚。

【输入格式】

第一行：三个整数 $n,m,p$，（$n,m,p\le 5000$），分别表示有 $n$ 个人，$m$ 个亲戚关系，询问 $p$ 对亲戚关系。

以下 $m$ 行：每行两个数 $M_i$，$M_j$，$1\le M_i,M_j\le n$，表示 $M_i$ 和 $M_j$ 具有亲戚关系。

接下来 $p$ 行：每行两个数 $P_i,P_j$，询问 $P_i$ 和 $P_j$ 是否具有亲戚关系。

【输出格式】

$p$ 行，每行一个 Yes 或 No。表示第 $i$ 个询问的答案为“具有”或“不具有”亲戚关系。

【示例一】

输入

6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

输出

Yes
Yes
No

---

模板题套了个壳子，把具有亲戚关系的两人合并到一个集合，合并完成之后询问亲戚关系相当于查询两个元素是否在一个集合里。

#include<iostream>using namespace std;const int N = 5010;
int pa[N];
int n, m, p;void init()
{for(int i = 1; i <= n; i++) pa[i] = i;
}int find(int x)
{if(x == pa[x]) return x;return pa[x] = find(pa[x]);
}void uni(int x, int y)
{int fx = find(x);int fy = find(y);pa[fx] = fy;
}bool issame(int x, int y)
{return find(x) == find(y);
}int main()
{cin >> n >> m >> p;init();int x, y;while(m--){cin >> x >> y;uni(x, y);}bool res;while(p--){cin >> x >> y;res = issame(x, y);if(res) cout << "Yes" << endl;else cout << "No" << endl;}return 0;
}

---

2. Lake Counting S ⭐⭐

【题目链接】

[P1596 USACO10OCT] Lake Counting S - 洛谷

【题目描述】

由于最近的降雨，水在农夫约翰的田地里积聚了。田地可以表示为一个 $N\times M$ 的矩形（$1\le N\le 100$；$1\le M\le 100$）。每个方格中要么是水（W），要么是干地（.）。农夫约翰想要弄清楚他的田地里形成了多少个水塘。一个水塘是由连通的水方格组成的，其中一个方格被认为与它的八个邻居相邻。给定农夫约翰田地的示意图，确定他有多少个水塘。

【输入格式】

第 $1$ 行：两个用空格分隔的整数：$N$ 和 $M$。

第 $2$ 行到第 $N+1$ 行：每行 $M$ 个字符，表示农夫约翰田地的一行。

每个字符要么是 W，要么是 .。

字符之间没有空格。

【输出格式】

第 $1$ 行：农夫约翰田地中的水塘数量。

【示例一】

输入

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

输出

3

【说明/提示】

输出详情：共有三个水塘：一个在左上角，一个在左下角，还有一个沿着右侧。

---

这道题可以用 BFS 解决，也可以用这里的并查集来解决。

利用并查集，遍历整个矩阵，每次遇到一个水坑时，就把这个水坑周围 8 个方向的水坑合并在一起。 最终判断一下一共有多少个集合。

小优化：可以不用把 8 个方向都合并，可以只把当前水坑的右、右下、下、左下 4 个部分合并即可。

#include<iostream>using namespace std;const int N = 105;
char grid[N][N];  // 田地
int pa[N * N];  // 并查集数组
int n, m;// 右、右下、下、左下 4 个方向
int dx[] = {1, 1, 0, -1};
int dy[] = {0, -1, -1, -1};void init()
{for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){// 把二维的坐标表示为一维的下标int t = (i - 1) * m + j;// 如果是水坑，就当作一个集合if(grid[i][j] == 'W') pa[t] = t;          }}
}int find(int x)
{if(x == pa[x]) return x;return pa[x] = find(pa[x]);
}void uni(int x, int y)
{int fx = find(x);int fy = find(y);pa[fx] = fy;
}int main()
{cin >> n >> m;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)cin >> grid[i][j];init();for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(grid[i][j] == '.') continue;// 遍历 4 个方向for(int k = 0; k < 4; k++){int x = i + dx[k];int y = j + dy[k];// 如果该方向没有越界并且也是水坑if(x > 0 && x <= n && y > 0 && y <= m && grid[x][y] == 'W'){// 就把这个方向的位置和当前的位置合并在一起，注意坐标要转成一维uni((i - 1) * m + j, (x - 1) * m + y);}}}}int cnt = 0;// 看有多少个根节点，就可以判断有多少个集合，也就是看有多少个元素的父节点指向自己for(int i = 1; i <= n * m; i++){if(pa[i] == i) cnt++;}cout << cnt << endl;return 0;
}

---

3. 程序自动分析 ⭐⭐⭐

【题目链接】

[P1955 NOI2015] 程序自动分析 - 洛谷

【题目描述】

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 $x_1,x_2,x_3,\cdots$ 代表程序中出现的变量，给定 $n$ 个形如 $x_i=x_j$ 或 $x_i\ne x_j$ 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：$x_1=x_2,x_2=x_3,x_3=x_4,x_4\ne x_1$，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

【输入格式】

输入的第一行包含一个正整数 $t$，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 $n$，表示该问题中需要被满足的约束条件个数。接下来 $n$ 行，每行包括三个整数 $i,j,e$，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 $e=1$，则该约束条件为 $x_i=x_j$。若$e=0$，则该约束条件为 $x_i\ne x_j$。

【输出格式】

输出包括 $t$ 行。

输出文件的第 $k$ 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 $k$ 个问题判定为可以被满足，NO 表示不可被满足。

【示例一】

输入

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出

NO
YES

【示例二】

输入

2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出

YES
NO

【说明/提示】

样例解释1

在第一个问题中，约束条件为：$x_1=x_2,x_1\ne x_2$。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：$x_1=x_2,x_1=x_2$。这两个约束条件是等价的，可以被同时满足。

样例说明2

在第一个问题中，约束条件有三个：$x_1=x_2,x_2=x_3,x_3=x_1$。只需赋值使得 $x_1=x_2=x_3$，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：$x_1=x_2,x_2=x_3,x_3=x_4,x_4\ne x_1$。由前三个约束条件可以推出 $x_1=x_2=x_3=x_4$，然而最后一个约束条件却要求 $x_1\ne x_4$，因此不可被满足。

数据范围

所有测试数据的范围和特点如下表所示：

---

离散化 + 并查集

读完这道题，很明显能想到用并查集来解决，相等条件就是把两个值所在集合合并成一个集合，不等条件就是要判断两个值是否处于一个集合中。由于这道题的 i 和 j 过大，我们没法开 $10^9$ 那么大的数组去存储这些数值，但是我们发现数据量 $n$ 并不是很大，所以我们可以采用离散化处理之后，再用并查集解决。

另外还有一个细节，在处理约束条件的时候，有可能是相等和不等条件交叉给出的，而我们需要先把所有的相等的信息维护完之后，再来判断不等的条件，这样才能判断正确。比如 $x_1=x_2$，$x_2\ne x_3$，$x_3=x_1$，如果从前往后依次判断的话输出 Yes，但是实际上条件矛盾了，我们应该把相等的信息处理完之后，再来判断不等的信息是否与已知的矛盾。那么如何处理这个问题呢？我们可以开一个数组，数组里面存结构体，结构体里面保存 $i$、$j$、$e$ 的信息即可。

// 离散化 + 并查集
#include<iostream>
#include<unordered_map>
#include<algorithm>using namespace std;
const int N = 1e5 + 10;
struct node{ int x, y, e; } a[N];  // 把每一组的 i, j, e 保存起来
int disc[2 * N];  // 离散化数组
int pa[2 * N];  // 并查集数组
int t, n;
unordered_map<int, int> id;  // <原始值, 离散化后的值>void init(int n)
{for(int i = 1; i <= n; i++) pa[i] = i;
}int find(int x)
{if(pa[x] == x) return x;return pa[x] = find(pa[x]);
}void uni(int x, int y)
{int fx = find(x);int fy = find(y);pa[fx] = fy;
}bool issame(int x, int y)
{return find(x) == find(y);
}int main()
{cin >> t;while(t--){id.clear();  // 记得清空数据cin >> n;int pos = 0;// 读入数据, 把 i 和 j 存入离散化数组for(int i = 1; i <= n; i++){cin >> a[i].x >> a[i].y >> a[i].e;disc[++pos] = a[i].x;disc[++pos] = a[i].y;}// 这里离散化的方式采用：排序 + 哈希表sort(disc + 1, disc + 1 + pos);int cnt = 0;  // 记录去重后的数据个数for(int i = 1; i <= pos; i++){int t = disc[i];if(id.count(t)) continue;id[t] = ++cnt;}init(cnt);  // 用离散化后的数据初始化并查集数组// 把所有相等的信息，用并查集维护起来for(int i = 1; i <= n; i++){node& nd = a[i];if(nd.e == 1) uni(id[nd.x], id[nd.y]);}// 合并完之后，再把不相等的信息拿出来判断是否合法int flag = 1;for(int i = 1; i <= n; i++){node& nd = a[i];if(nd.e == 0){bool t = issame(id[nd.x], id[nd.y]);if(t) flag = 0;}}if(flag) cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}