做淘宝网站买个模版可以吗免费体验服务器

目录

搜索二维矩阵Ⅱ

题目描述

题解

解法一：暴力搜索

C++ 代码实现

复杂度分析

解法二：二分查找

C++ 代码实现

复杂度分析

解法三：Z字形查找

算法核心思想

算法步骤详解

C++ 代码实现

复杂度分析

---

搜索二维矩阵Ⅱ

题目描述

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。 每列的元素从上到下升序排列。

示例 1：

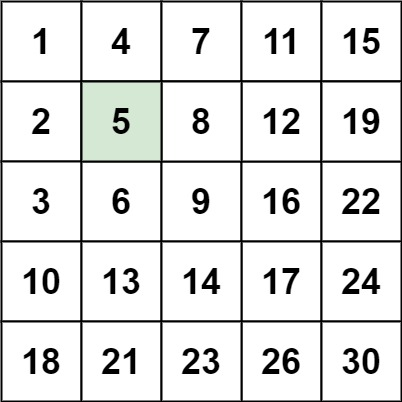
输入：matrix = [ [1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30] ], target = 5
输出：true

示例 2：

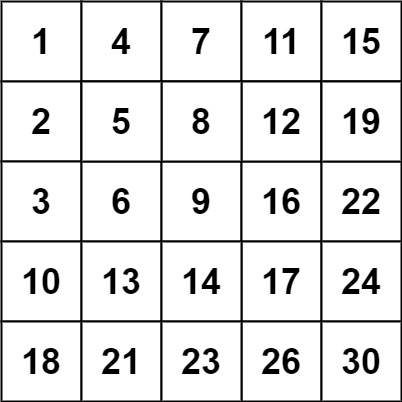
输入：matrix = [ [1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30] ], target = 20 输出：false

提示：
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列

题解

解法一：暴力搜索

暴力搜索的思路是遍历矩阵的所有元素，并判断当前元素是否等于目标值。时间复杂度为 O(mn)。

C++ 代码实现

class Solution:{
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();int n = matrix[0].size();for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == target) {return true;}}}return false;
}
};

复杂度分析

• 时间复杂度：O(mn)，遍历矩阵的所有元素。
• 空间复杂度：O(1)，不使用额外空间。

解法二：二分查找

由于矩阵 matrix 中每一行的元素都是升序排列的，因此我们可以对每一行都使用一次二分查找，判断 target 是否在该行中，从而判断 target 是否出现。

C++ 代码实现

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for (const auto& row : matrix) {if(binary_search(row.begin(), row.end(), target)) {return true;  }}return false;}};

复杂度分析

• 时间复杂度：O(mlogn)，对每一行使用一次二分查找，时间复杂度为 O(logn)。
• 空间复杂度：O(1)，不使用额外空间。

解法三：Z字形查找

算法核心思想

Z字形查找是一种线性时间复杂度的搜索算法，专门用于搜索行列都有序的二维矩阵。
它的核心思想是： 从矩阵的右上角开始搜索 利用矩阵的有序性质，每次可以排除一整行或一整列 搜索路径形成"Z"字形，因此得名

算法步骤详解

步骤 1: 初始化位置
从右上角 (0, n-1) 开始，这个位置有特殊性质：
向左移动：值变小
向下移动：值变大
步骤 2: 比较与移动
if (matrix[x][y] == target) → 找到目标，返回 true
if (matrix[x][y] > target) → 当前值太大，向左移动 (y--)
if (matrix[x][y] < target) → 当前值太小，向下移动 (x++)
步骤 3: 边界检查
如果超出边界 (x >= m || y < 0)，说明目标不存在

C++ 代码实现

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size(), n = matrix[0].size();int x = 0, y = n - 1; // 从右上角开始while (x < m && y >= 0) {if (matrix[x][y] == target) {return true; // 找到目标}if (matrix[x][y] > target) {--y; // 当前值太大，向左移动} else {++x; // 当前值太小，向下移动}}return false; // 超出边界，未找到}
};

复杂度分析

• 时间复杂度：O(m+n)。在搜索的过程中，如果我们没有找到 target，那么我们要么将 y 减少 1，要么将 x 增加 1。由于 (x,y) 的初始值分别为 (0,n−1)，因此 y 最多能被减少 n 次，x 最多能被增加 m 次，总搜索次数为 m+n。在这之后，x 和 y 就会超出矩阵的边界。

• 空间复杂度：O(1)，不使用额外空间。