LeetCode算法日记 - Day 102: 不相交的线

目录

1. 不相交的线

1.1 题目解析

1.2 解法

1.3 代码实现

---

1. 不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

•  nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

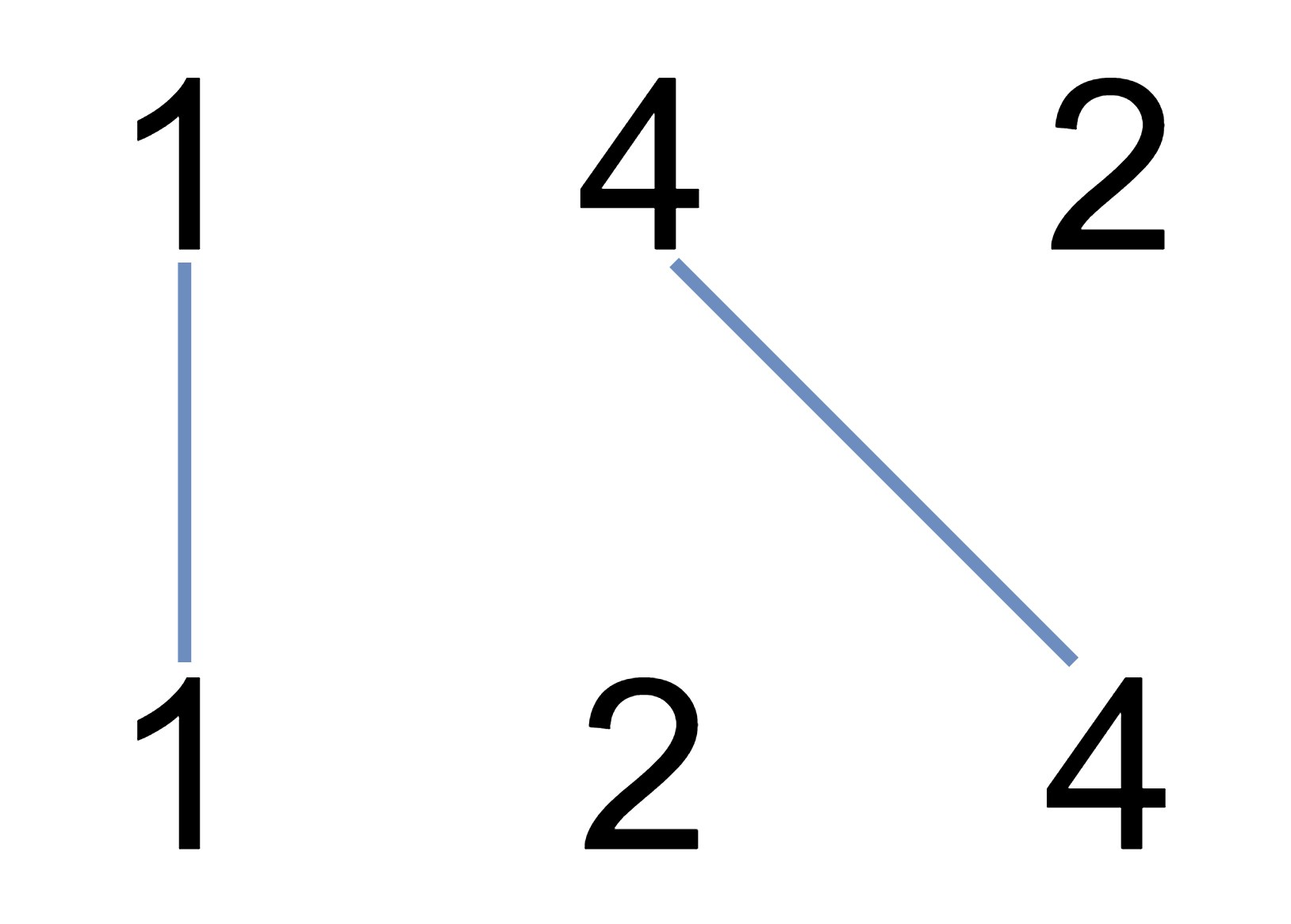
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

• 1 <= nums1.length, nums2.length <= 500
• 1 <= nums1[i], nums2[j] <= 2000

1.1 题目解析

题目本质
这是一个最长公共子序列（LCS）的变形问题。题目要求在两个数组间连线，使得连线不相交且连线数量最大化。

常规解法
最直观的想法是使用回溯法，尝试所有可能的连线组合，对每种组合检查是否存在相交，然后取连线数量的最大值。

class Solution {private int maxLines = 0;public int maxUncrossedLines(int[] nums1, int[] nums2) {backtrack(nums1, nums2, 0, 0, 0);return maxLines;}private void backtrack(int[] nums1, int[] nums2, int i, int j, int lines) {if (i >= nums1.length || j >= nums2.length) {maxLines = Math.max(maxLines, lines);return;}// 不连当前位置backtrack(nums1, nums2, i + 1, j, lines);backtrack(nums1, nums2, i, j + 1, lines);// 如果当前位置可以连线if (nums1[i] == nums2[j]) {backtrack(nums1, nums2, i + 1, j + 1, lines + 1);}}
}

问题分析
回溯法的时间复杂度是指数级的O(2^(m+n))，当数组长度达到500时会超时。需要找到更高效的解法。

思路转折
关键洞察是不相交的连线等价于最长公共子序列。如果我们按照nums1和nums2的顺序依次考虑每个元素，那么不相交的连线必然保持相对顺序不变。要想高效求解 → 必须使用动态规划 → 转化为LCS问题。

1.2 解法

算法思想
使用动态规划求解最长公共子序列。定义dp[i][j]表示nums1前i个元素和nums2前j个元素能连接的最大线数。

递推公式：

• 如果nums1[i-1] == nums2[j-1]：dp[i][j] = dp[i-1][j-1] + 1

• 否则：dp[i][j] = max(dp[i-1][j], dp[i][j-1])

步骤拆解

i）创建二维DP数组，大小为(n+1) × (m+1)，初始化为0

ii）双重循环遍历两个数组

iii）如果当前元素相等，从左上角转移并加1

iv）如果不相等，从上方或左方取最大值

v）返回dp[n][m]作为最终答案

易错点

• 数组索引问题：DP数组是(n+1) × (m+1)大小，但原数组访问时要用i-1和j-1

• 边界初始化：第0行和第0列应该保持为0，表示空数组的情况

• 状态转移理解：要明确dp[i-1][j]和dp[i][j-1]分别表示跳过当前nums1或nums2元素的情况

1.3 代码实现

class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int n = nums1.length;int m = nums2.length;int[][] dp = new int[n + 1][m + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (nums1[i - 1] == nums2[j - 1]) {// 相等时从对角线转移并加1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 不相等时取上方和左方的最大值dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[n][m];}
}

复杂度分析

• 时间复杂度：O(n × m)，需要填充整个DP表格

• 空间复杂度：O(n × m)，使用了二维DP数组存储状态