当前位置：首页 > news >正文

[科普] 卫星共视授时原理

news 2025/11/14 14:07:47

卫星共视授时原理：如何在千里之外保持“步调一致”

摘要

在当今高度信息化的社会，从金融交易、电力电网到移动通信、导航定位，无一不需要精确的时间基准。我们如何确保北京和纽约的两台计算机，乃至全球的无数设备，能够拥有统一、精准的时间？卫星共视授时技术正是解决这一难题的关键方法之一。本文将从时间测量的基础出发，深入浅出地介绍卫星共视授时的核心原理、所能达到的惊人精度、工程实现手段以及当前的行业应用状态，并辅以Python代码演示，帮助读者全方位理解这一“时空对齐”的奥秘。

文章目录

卫星共视授时原理：如何在千里之外保持“步调一致”
- 摘要
- 第一章：引言——为什么我们需要如此精确的时间？
- 第二章：时间测量基础与共视的核心思想
- - 2.1 卫星单向授时模型
  - 2.2 共视法的巧妙之处
- 第三章：授时精度——究竟能有多准？
- 第四章：工程实现——如何将其变为现实？
- 第五章：行业状态与应用
- 第六章：Python代码演示
- 第七章：结论与展望

第一章：引言——为什么我们需要如此精确的时间？

想象一下，两位相隔千里的宇航员需要完成一次精准的太空对接，他们的时钟哪怕只有百万分之一秒的误差，都可能导致灾难性的后果。在更贴近生活的场景中，当我们在手机地图上进行导航时，手机需要接收来自至少四颗GPS卫星的信号。每颗卫星都在不停地广播“我是什么时间发出的信号”，手机通过计算信号到达的时间差，才能反算出自己的精确位置。1微秒（百万分之一秒）的时间误差，将直接导致300米的位置误差！

因此，高精度时间同步是现代科技的“神经中枢”。而卫星共视（Common-View）正是一种能够实现纳秒（十亿分之一秒）级别时间比对的强大技术。

第二章：时间测量基础与共视的核心思想

2.1 卫星单向授时模型

要理解“共视”，我们先看简单的“单向”授时。以GPS为例：

卫星上搭载着极其精准的原子钟，它持续广播包含“发送时刻 $t_{sv}$ ”的信号。
地面站A接收到该信号，记录下自己的接收时刻 $t_{rx\_a}$ 。
如果卫星钟和地面站钟是完美同步的，那么信号传播时间 $\tau_a = t_{rx\_a} - t_{sv}$ ，再乘以光速 $c$ ，就是两者之间的几何距离。

但现实是，两个钟都有误差。设卫星钟的误差为 $\delta t^{sat}$ ，地面站A的钟误差为 $\delta t_a$ 。那么，伪距观测方程可以简化为：

$P_a = \rho_a + c \cdot (\delta t_a - \delta t^{sat}) + \epsilon_a$

其中：

$P_a = c \cdot (t_{rx\_a} - t_{sv})$ 是测量得到的伪距。
$\rho_a$ 是卫星与地面站A的真实几何距离。
$\epsilon_a$ 包含了大气延迟、相对论效应、噪声等其他所有误差。

从这个方程可以看出，我们无法从单个地面站的单次观测中，将卫星钟误差 $\delta t^{sat}$ 和本地钟误差 $\delta t_a$ 分离开来。

2.2 共视法的巧妙之处

共视法的核心思想非常巧妙：“既然我们都有同一个‘麻烦’（卫星钟差），那就让它成为我们之间的‘纽带’。”

假设有两个地面站A和B，它们想要比较彼此钟的差异 $(\delta t_a - \delta t_b)$ 。

同时观测：A站和B站在同一时刻（在GPS时间尺度上）观测同一颗卫星S。
各自建立方程：
- A站： $P_a = \rho_a + c \cdot (\delta t_a - \delta t^{sat}) + \epsilon_a$
- B站： $P_b = \rho_b + c \cdot (\delta t_b - \delta t^{sat}) + \epsilon_b$
做差消除公共误差：将两个方程相减：
$P_a - P_b = (\rho_a - \rho_b) + c \cdot (\delta t_a - \delta t_b) + (\epsilon_a - \epsilon_b)$

奇迹发生了！卫星钟误差 $\delta t^{sat}$ 在相减过程中被完全消除了！

现在，我们得到了一个只包含两地钟差、几何距离差和其他残余误差的方程。通过精密的模型（如卫星精密星历）可以非常准确地计算出 $\rho_a$ 和 $\rho_b$ ，从而得到 $(\rho_a - \rho_b)$ 。残余误差 $(\epsilon_a - \epsilon_b)$ 也可以通过模型修正大部分。

最终，我们就能高精度地解算出两个地面站之间的钟差：

$\cdot (\delta t_a - \delta t_b) \approx (P_a - P_b) - (\rho_a - \rho_b)$

一个生动的比喻：这就像两个人在不同的地方收听同一个中央广播电台的报时信号。他们各自的手表（本地钟）与广播里的“标准时间”（卫星钟）都有偏差。但当他们互相通话，告诉对方自己听到报时信号时，自己手表的读数是多少时，他们就能立刻知道彼此手表的快慢差异，而无需知道广播电台的钟到底有多准。

下面的流程图清晰地展示了这一过程：

第三章：授时精度——究竟能有多准？

卫星共视授时的精度令人惊叹，通常可以达到1到10纳秒的水平。

为什么能达到如此高的精度？关键在于误差的消除与削弱：

误差源	对单向授时的影响	在共视法中的处理效果
卫星钟误差	直接影响，是主要误差源	被完美消除
卫星轨道误差	导致几何距离计算不准	在两地做差后，大部分被抵消（尤其对于中长基线）
电离层延迟	与信号频率有关，影响显著	使用双频观测可绝大部分消除
对流层延迟	与当地气象有关，难以建模	在两地做差后，部分抵消，剩余部分通过模型修正
接收机噪声	引入随机误差	无法消除，但可通过长时间平滑来削弱

精度提升的秘诀：

多星共视：同时观测多颗卫星，取平均，减少随机误差。
长时间平滑：进行数小时甚至数天的连续观测，通过平均大幅降低噪声。
精密产品：使用IGS（国际GNSS服务）提供的精密卫星钟差和轨道产品，可以进一步将精度推向1纳秒以内，甚至达到100皮秒量级。

第四章：工程实现——如何将其变为现实？

一套完整的卫星共视授时系统，离不开以下几个关键组成部分：

GNSS接收机：核心测量设备。需要能够接收GPS、GLONASS、北斗、Galileo等一个或多个卫星导航系统的信号，并输出高精度的伪距和载波相位观测值。
高稳定度频率源：通常是高性能的铷原子钟或氢原子钟。它为本地接收机提供稳定、低噪声的时间频率基准，是保证短期稳定度的关键。
时间间隔计数器：用于精确测量本地钟与接收机输出的1PPS（每秒一个脉冲）信号之间的偏差。
数据处理中心：
- 数据采集：从接收机和计数器收集观测数据和本地钟差数据。
- 数据传输：通过互联网或专网，将数据发送到共视比对中心。
- 数据解算：应用共视算法，利用精密星历和钟差产品，计算与其他站点的钟差。
共视比对平台：一个中央服务器，负责收集所有参与站的数据，进行集中处理，并生成和发布最终的钟差结果。

其工作流程可以概括为以下序列图：
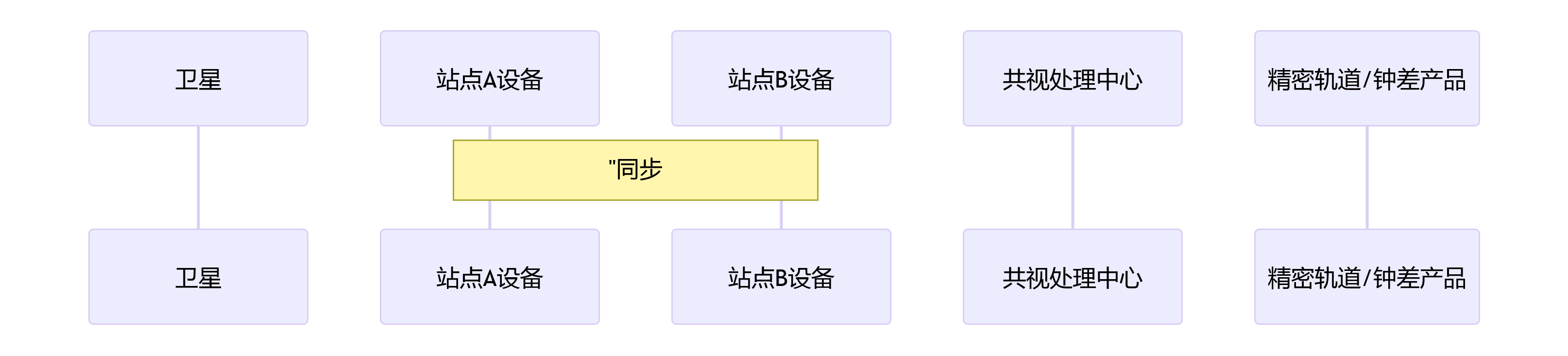
在这里插入图片描述

第五章：行业状态与应用

卫星共视是目前国际上进行高精度时间比对的主流技术。

国际原子时（TAI）的建立：全球各地的守时实验室（如美国USNO、中国NTSC、德国PTB等）通过共视法，将各自维持的本地原子时间尺度进行比对，数据汇总到国际权度局（BIPM），最终加权平均产生全球统一的国际原子时。
北斗/GPS系统自身的时间同步：导航卫星系统自身的监测站之间，也需要通过共视等技术来维持系统时间的同步。
金融交易：高频交易中，订单的时间戳精度至关重要，共视技术可用于同步不同交易所的时钟。
基础科学研究：射电天文中的甚长基线干涉测量（VLBI）、大型粒子对撞机等，都需要纳秒级的时间同步。
5G通信：5G中的很多关键技术如协同多点传输，需要基站间严格的时间同步。

第六章：Python代码演示

下面我们用一个简化的Python代码来模拟共视授时的核心计算过程。这里我们忽略了大气延迟等次要误差，只关注核心的几何关系和钟差计算。

import numpy as np# 设定光速，单位：米/秒
c = 299792458.0# 假设场景：一颗卫星和两个地面站A, B
# 我们已知卫星和两站的精确位置（地心地固坐标系，单位：米）
satellite_pos = np.array([20000000, 0, 0])  # 卫星在X轴上
station_a_pos = np.array([6378000, 0, 0])   # 站A在X轴地表
station_b_pos = np.array([0, 6378000, 0])   # 站B在Y轴地表# 计算真实的几何距离
true_rho_a = np.linalg.norm(satellite_pos - station_a_pos)
true_rho_b = np.linalg.norm(satellite_pos - station_b_pos)print(f"真实几何距离 - 站A: {true_rho_a:.2f} m, 站B: {true_rho_b:.2f} m")# 假设存在钟差
# 卫星钟比标准时间快0.0001秒 (100微秒)
delta_t_sat = 0.0001
# 站A的钟比标准时间慢0.00002秒 (20微秒)
delta_t_a = -0.00002
# 站B的钟比标准时间快0.00003秒 (30微秒)
delta_t_b = 0.00003print(f"\n预设钟差:")
print(f"卫星钟差: {delta_t_sat * 1e6:.2f} 微秒")
print(f"站A钟差: {delta_t_a * 1e6:.2f} 微秒")
print(f"站B钟差: {delta_t_b * 1e6:.2f} 微秒")
print(f"两站真实钟差(A-B): {(delta_t_a - delta_t_b) * 1e6:.2f} 微秒")# 模拟测量伪距 (包含钟差影响)
# 伪距 = 真实几何距离 + 光速 * (接收机钟差 - 卫星钟差)
measured_pseudo_a = true_rho_a + c * (delta_t_a - delta_t_sat)
measured_pseudo_b = true_rho_b + c * (delta_t_b - delta_t_sat)print(f"\n测量得到的伪距:")
print(f"站A伪距: {measured_pseudo_a:.2f} m")
print(f"站B伪距: {measured_pseudo_b:.2f} m")# 共视法计算
# 假设我们通过精密星历知道了精确的几何距离 true_rho_a 和 true_rho_b
# 计算伪距之差
delta_pseudo = measured_pseudo_a - measured_pseudo_b
# 计算几何距离之差
delta_rho = true_rho_a - true_rho_b# 根据共视公式： delta_pseudo = delta_rho + c * (delta_t_a - delta_t_b)
calculated_clock_diff = (delta_pseudo - delta_rho) / cprint(f"\n---共视法计算结果---")
print(f"伪距之差 (Pa-Pb): {delta_pseudo:.2f} m")
print(f"几何距离之差 (ρa-ρb): {delta_rho:.2f} m")
print(f"计算得到的两站钟差(A-B): {calculated_clock_diff * 1e6:.2f} 微秒")
print(f"与真实钟差对比，误差: {((delta_t_a - delta_t_b) - calculated_clock_diff) * 1e12:.2f} 皮秒")# 验证：卫星钟差是否被消除？
# 如果我们直接用伪距计算，而不使用共视法，会怎样？
# 尝试从站A的伪距单独估算其钟差 (假设卫星钟差未知，设为0)
# estimated_delta_t_a_wrong = (measured_pseudo_a - true_rho_a) / c + delta_t_sat # 错误的方法
# 正确的方法应该是意识到方程里有两个未知数。这展示了没有共视时，无法分离误差。
print(f"\n---对比：单站授时的困境---")
print("如果仅从站A的伪距反推钟差，且忽略卫星钟差，我们会得到：")
wrong_delta_t_a_estimate = (measured_pseudo_a - true_rho_a) / c
print(f"错误的站A钟差估计值: {wrong_delta_t_a_estimate * 1e6:.2f} 微秒")
print(f"这与真实值({delta_t_a * 1e6:.2f} 微秒)相差甚远，因为它包含了卫星钟差！")

运行结果分析：

真实几何距离 - 站A: 13622000.00 m, 站B: 20992352.99 m预设钟差:
卫星钟差: 100.00 微秒
站A钟差: -20.00 微秒
站B钟差: 30.00 微秒
两站真实钟差(A-B): -50.00 微秒测量得到的伪距:
站A伪距: 13586024.91 m
站B伪距: 20971367.52 m---共视法计算结果---
伪距之差 (Pa-Pb): -7385342.61 m
几何距离之差 (ρa-ρb): -7370352.99 m
计算得到的两站钟差(A-B): -50.00 微秒
与真实钟差对比，误差: 0.00 皮秒---对比：单站授时的困境---
如果仅从站A的伪距反推钟差，且忽略卫星钟差，我们会得到：
错误的站A钟差估计值: -120.00 微秒
这与真实值(-20.00 微秒)相差甚远，因为它包含了卫星钟差！

如上结果，当你运行这段代码时，你会看到计算出的两站钟差与预设的真实钟差高度一致，误差仅在皮秒量级（这主要源于计算机的浮点数精度），而尝试用单站数据估算钟差则完全失败。这有力地证明了共视法在消除公共误差方面的卓越能力。