NGO-VMD北方苍鹰算法优化变分模态分解+皮尔逊系数+小波阈值降噪+信号重构，MATLAB代码

代码功能概述

主要功能

该代码实现了一个基于北方苍鹰优化算法(NGO)优化的变分模态分解(VMD)信号处理，主要功能包括：

• 信号的自适应分解与参数优化
• 模态分量的相关性分析与降噪处理
• 多维度可视化与结果评估
  
  

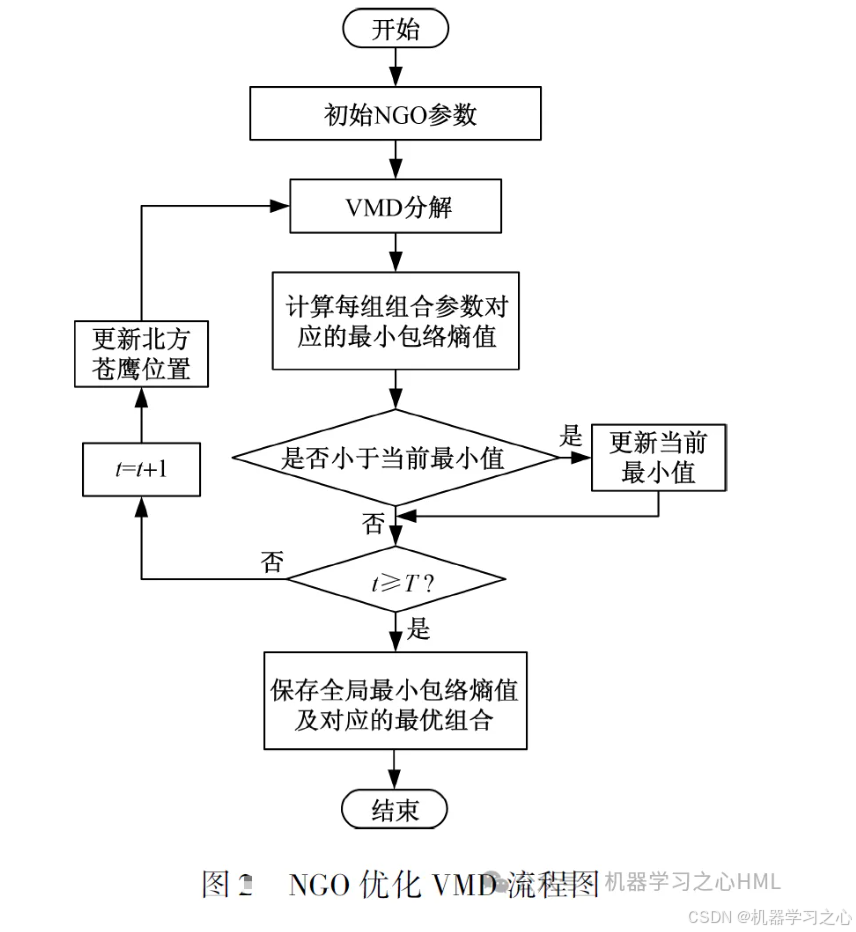
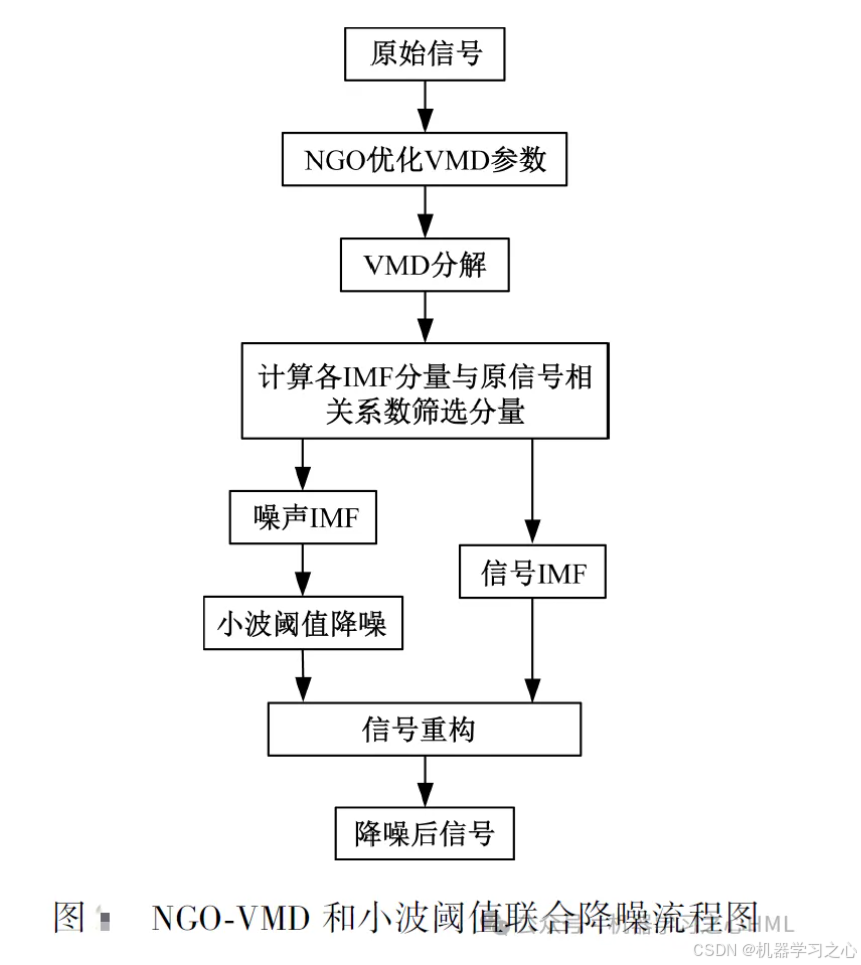
算法步骤

1. 数据准备阶段

数据导入 → 参数初始化 → 适应度函数定义

2. 参数优化阶段

NGO算法初始化 → 迭代寻优 → 最优参数输出↓
[K值, α值]优化

3. 信号处理阶段

VMD分解 → 模态分量分析 → 频谱分析↓
相关性计算 → 阈值分类 → 小波降噪↓
信号重构 → 结果对比

4. 可视化分析阶段

收敛曲线 → 时域分解图 → 频域谱图↓
参数优化过程 → 3D视图 → 降噪效果对比

技术路线

核心算法组合

北方苍鹰优化算法(NGO) + 变分模态分解(VMD) + 小波阈值降噪

技术流程

1. 优化层：NGO算法自适应寻找VMD最优参数
2. 分解层：VMD将信号分解为多个本征模态函数(IMF)
3. 筛选层：基于皮尔逊相关系数筛选有效分量
4. 降噪层：小波阈值处理噪声分量
5. 重构层：信号恢复与质量评估

公式原理

1. VMD变分问题

$$min\sum _k\Vert {\partial }_t[(\delta (t)+j/\pi t)\ast u_k(t)]e^{(}-j{\omega }_{k}t){\Vert }^2$$
$$s.t.\sum _k{u}_k=f(t)$$
其中：

• $u_k$：第k个模态分量
• ${\omega }_k$：中心频率
• $\alpha$：惩罚因子（控制带宽）

2. 包络熵适应度函数

$$E=-\sum p_{i}log{p}_i$$
$$p_i=a(i)/\sum a(j)$$
其中$a(i)$为包络信号，熵值越小表示信号越纯净。

3. 小波阈值函数

• 软阈值：${\eta }_{s}oft=sign(x)(|x|-T{)}_{+}$
• 硬阈值：${\eta }_{h}ard=x\cdot I(|x|>T)$
  阈值计算：$T=\sigma \surd (2lnN)$

参数设定

VMD参数

参数	值	说明
tau	0	噪声容忍度
dc	0	直流分量
init	1	初始化方式
tol	1e-7	收敛容差

NGO优化参数

参数	值	范围
种群数量	3	-
最大迭代	10	-
K值范围	[2, 12]	模态数
α值范围	[600, 3000]	惩罚因子

小波降噪参数

参数	值	说明
小波基	‘db1’	Daubechies小波
分解层数	2	分解尺度
阈值规则	sqtwolog	通用阈值

运行环境

软件要求

• 平台：MATLAB R2018b或更高版本
• 必要工具箱：
  • 信号处理工具箱
  • 优化工具箱
  • 统计和机器学习工具箱

硬件建议

• 内存：≥8GB
• 处理器：Intel i5或同等性能
• 存储空间：≥1GB可用空间

依赖函数

NGO()          % 北方苍鹰优化算法
VMD()          % 变分模态分解
hua_fft()      % FFT计算函数
plot3imf()     % 3D可视化函数
wavedec()      % 小波分解
wdencmp()      % 小波降噪

应用场景

1. 机械故障诊断

• 轴承故障检测：振动信号分解与特征提取
• 齿轮箱监测：故障频率识别与早期预警
• 旋转机械分析：不平衡、不对中故障诊断

2. 生物医学信号处理

• 心电信号分析：QRS波检测与噪声去除
• 脑电信号处理：节律分离与特征提取
• 肌电信号分解：运动单元动作电位分析

3. 电力系统监测

• 电能质量分析：谐波检测与间谐波分离
• 故障录波分析：暂态信号特征提取
• 负荷监测：用电设备识别与分类

4. 地质勘探

• 地震信号处理：反射波分离与噪声压制
• 声波测井：地层界面识别与特征提取

5. 金融时间序列

• 股价波动分析：多尺度特征提取
• 风险预警：异常波动检测与模式识别

技术优势

1. 自适应性：自动优化VMD参数，避免人工试错
2. 鲁棒性：结合多种降噪方法，适应不同噪声环境
3. 可视化：提供全面的分析视图，便于结果解读
4. 灵活性：模块化设计，易于扩展和修改

该代码特别适用于非平稳、非线性信号的精细化分析和特征提取，在工程诊断和科学研究中具有广泛的应用价值。

部分源码Node {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
ily: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
% 清理工作区，关闭所有图形窗口，清空命令窗口
clear all ;
clc;
close all;
%% 导入数据
fs = 1024; % 采样频率，用于频谱图
% 读取Excel数据文件，并进行转置（如果数据是列数据）
DATA.data = xlsread('data.xlsx')'; 
DATA.tau = 0;                    % VMD参数：时间步长
DATA.dc = 0;                     % VMD参数：直流分量
DATA.init = 1;                   % VMD参数：初始化方式
DATA.tol = 1e-7;                 % VMD参数：容忍度
%% 定义适应度函数SearchAgents_no = 3;            % 种群数量
Max_iteration = 10;             % 最大迭代次数
dim = 2;                        % 优化参数个数（K值和alpha值）
lb = [600, 2];                  % 参数下界 [alpha, K]
ub = [3000, 12];                % 参数上界 [alpha, K]
%% 执行参数寻优（使用NGO算法）
[Best_score, Best_pos, Convergence_curve, ak] = NGO(SearchAgents_no, Max_iteration, lb, ub, dim, fitness);
%% 显示最优参数并执行VMD分解
disp(['最优K值为：', num2str(round(Best_pos(1,2)))])
disp(['最优alpha值为：', num2str(round(Best_pos(1,1)))])
disp(['最优指标为：', num2str(Best_score)])
% 使用最优参数执行VMD分解
[u, u_hat, omega] = VMD(DATA.data, round(Best_pos(1,1)), DATA.tau, round(Best_pos(1,2)), DATA.dc, DATA.init, DATA.tol);

完整代码私信NGO-VMD北方苍鹰算法优化变分模态分解+皮尔逊系数+小波阈值降噪+信号重构，MATLAB代码