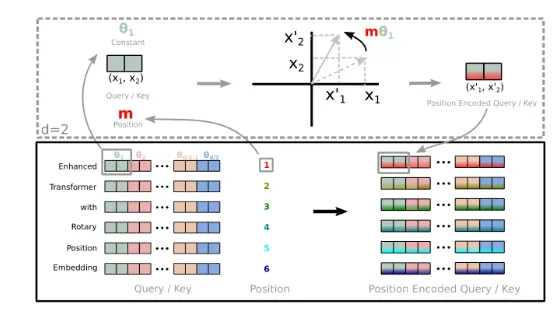
旋转位置编码(Rotary Position Embedding,RoPE)
目录
1、复数
2、绝对位置编码
2.1 固定的
2.2 可学习的
3、相对位置编码
4、旋转位置编码
4.1 旋转矩阵
4.2 二维空间的旋转矩阵
4.3 多维空间的旋转矩阵
https://arxiv.org/pdf/2104.09864
旋转位置编码(Rotary Position Embedding,RoPE)是一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。而目前很火的 LLaMA、GLM 模型也是采用该位置编码方式。是否使用RoPE,需要看具体的任务,如处理有明显的顺序或者空年依赖性的任务,如视频插帧,多分辨率生成等。RoPE可以有效的引入位置信息,帮助理解元素间的相对关系。RoPE通过旋转矩阵对绝对位置进行编码,同时在自注意力机制中显式融入相对位置依赖性。RoPE具备三大优势:
(1)长度灵活:支持可变序列长度;
(2)距离衰减:相对距离增大时token间依赖性的衰减特性;
(3)线性兼容:可以将相对位置信息直接编码到线性注意力(Linear Attention)机制中,从而提升计算效率。
1、复数
复数(Complex Number)是一种数学概念,表示为
![]()
在这个表达式中:
- a被称为复数的实部 ,它是复数的实数部分。
- b被称为复数的 虚部,它是复数中伴随虚数单位i的系数。
复数不仅可以通过标准形式a+ib来表示,还可以使用极坐标形式,复数的极坐标形式为:
![]()
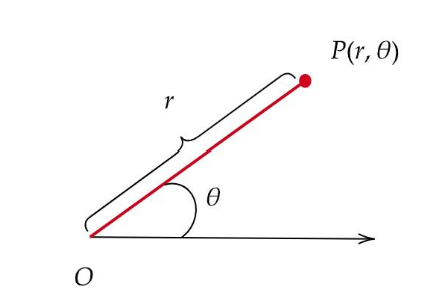
其中:r=|z|是复数的模,也即复数距离原点的欧几里得距离。它的计算公式为![]() 。
。
θ是复数的幅角(或称为辐角、相位角),它是复数与正实轴之间的夹角。
欧拉还提出了著名的欧拉公式:
![]()
2、绝对位置编码
2.1 固定的
正弦位置编码利用不同频率的正弦和余弦函数为每个位置生成唯一模式。编码公式如下:
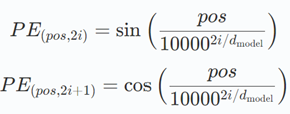
其中:
pos 是词的位置,
i 是维度索引。
此方法的优势在于能够泛化到训练时未见的序列长度,灵活处理不同规模的输入。
2.2 可学习的
随机初始化嵌入向量,并在训练过程中更新。GPT和BERT等模型均采用Embedding。其缺点是泛化能力受限——若序列长度超出训练时的最大位置数,由于在查找表中没有对应选项,模型将无法处理超出的位置。
无论是可学习的还是固定的,绝对位置编码的常规做法是会计算一个位置编码向量 P,加到词嵌入 X上,然后再乘以对应的变换矩阵,位置编码的维度与词嵌入的维度相同。
3、相对位置编码
与绝对位置编码不同,相对位置编码不是直接叠加位置向量,而是创建反映token间相对距离的矩阵。例如,若token i位于位置3,token j位于位置5,则相对位置为2。
相对位置嵌入会修改注意力分数,以包含关于相对位置的信息。在自注意力机制中,注意力分数是根据一对标记之间的位置计算出来的,相对位置嵌入根据相对位置在注意力分数中添加一个偏置项,或者通过为每个可能的相对距离引入一个可学习的嵌入。
这种方法的实现为在注意力得分中添加一个相对位置偏差B。
![]()
以单个token的计算为例,Qi和Kj分别为token i 和token j的“query”值和“key”值,dk是“key”向量的维度,Bij是相对位置j−i的偏置。
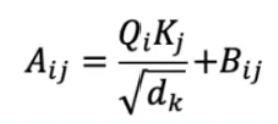
4、旋转位置编码
旋转位置嵌入(Rotary Positional Embedding, RoPE)结合了绝对与相对位置编码的优点,通过旋转高维空间中的向量编码位置信息,实现位置编码。其核心思想是为每个位置生成唯一的旋转矩阵,使模型能捕获相对位置关系。
旋转量取决于单词/token在序列中的位置。任意两个单词之间的相对位置可以通过一个单词的向量相对于另一个单词的旋转量来轻松计算。因此,虽然每个单词根据其绝对位置获得旋转量,模型可以轻松计算出相对位置。
RoPE有几个优点:
- 比绝对位置嵌入更有效地处理长序列,
- 自然地将绝对位置嵌入和相对位置嵌入二者结合到一起。
- 计算效率高,易于实现。
给定一个token,RoPE会根据其在序列中的位置对其对应的key和query向量进行旋转,并通过用旋转矩阵乘以向量来实现旋转,使用旋转后的key和query向量以计算注意力分数。
4.1 旋转矩阵
旋转矩阵(Rotation matrix)是在乘以一个向量的时候有改变向量的方向但不改变大小。
设M是任何维的一般旋转矩阵:![]() 。
。
(1)两个向量的点积(内积)在它们都被一个旋转矩阵操作之后保持不变:
![]()
(2)旋转矩阵的逆矩阵是它的转置矩阵:
![]()
(3)一个矩阵是旋转矩阵,当且仅当它是正交矩阵并且它的行列式是单位一。正交矩阵的行列式是 ±1;如果行列式是 −1,则它包含了一个反射而不是真旋转矩阵。
(4)旋转矩阵是正交矩阵,如果它的列向量形成![]() 的一个正交基,就是说在任何两个列向量之间的标量积是零(正交性)而每个列向量的大小是单位一(单位向量)。
的一个正交基,就是说在任何两个列向量之间的标量积是零(正交性)而每个列向量的大小是单位一(单位向量)。
(5)任何旋转向量可以表示为斜对称矩阵A的指数:
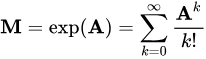
4.2 二维空间的旋转矩阵
在二维空间中,旋转可以用一个单一的角 θ定义。作为约定,正角表示逆时针旋转。旋转矩阵如下所示:
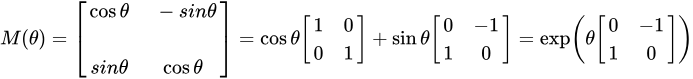
如果将二维旋转矩阵上乘以一个向量,那么它改变了向量的角度,并保持了向量的长度。将旋转矩阵乘以key和query向量。
词嵌入向量 xm表示第 m个 token 对应的词量,xn示第 n个 token 对应的词向量,qm为第m个token对应的query向量,kn为第n个token对应的key向量,qm和kn的内积操作用g来表示,g函数的输入是词嵌入向量 xm , xn和它们之间的相对位置 m-n,假设词嵌入的维度d=2:
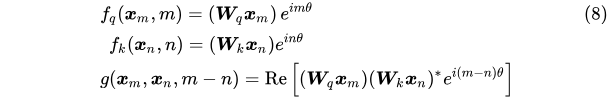
Re 表示复数的实部。
fq可以展开成 下面 的形式:
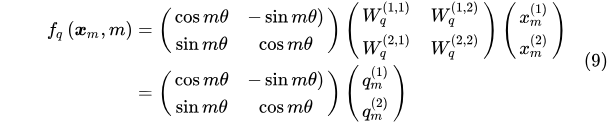
从形式上看就是 query 向量乘以了一个旋转矩阵,这也是为什么叫做旋转位置编码的原因。同理可以展开fk:
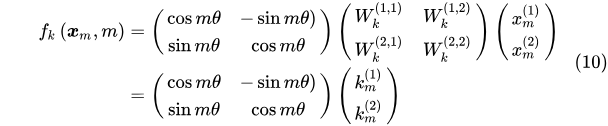
则g(xm ,xn,m-n)为:
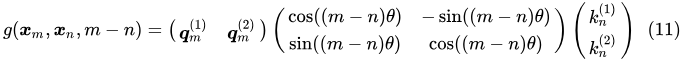
4.3 多维空间的旋转矩阵
将2维推广到任意维度,维度用d表示,query和key的计算方式为下:
![]()
内积满足线性叠加性,因此任意偶数维的RoPE,我们都可以表示为二维情形的拼接,即:
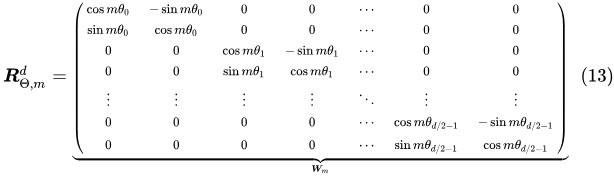
![]()
包含相对位置信息的Self-Attetion为:
![]()
![]()
由于旋转矩阵的稀疏性,直接用矩阵乘法来实现会很浪费算力,推荐通过下述方式来实现 RoPE:

RoPE 的 self-attention 操作的流程是:
- 对于 token 序列中的每个词嵌入向量,首先计算其对应的 query 和 key 向量;
- 然后对每个 token 位置都计算对应的旋转位置编码;
- 接着对每个 token 位置的 query 和 key 向量的元素按照 两两一组 应用旋转变换;
- 最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果。