当前位置：首页 > news >正文

深度学习：RMSprop 优化算法详解

news 2025/11/14 11:46:42

✅ 一、什么是 RMSprop？

RMSprop（Root Mean Square Propagation） 是一种自适应学习率的优化算法，由 Geoffrey Hinton 提出，用于解决梯度下降中不同方向梯度变化不一致的问题。

🔍 核心目标：
通过动态调整每个参数的学习率，使训练过程更稳定、更快收敛。

✅ 二、背景：为什么需要 RMSprop？

在标准梯度下降（GD）或随机梯度下降（SGD）中：

如果某个方向的梯度很大 → 参数更新幅度过大；
如果某个方向的梯度很小 → 参数几乎不动；
导致训练效率低，甚至在某些方向上“卡住”。

🎯 例如：在椭圆形损失函数中，沿长轴方向梯度小，短轴方向梯度大，SGD 会“横跳”而难以快速下降。

✅ 三、RMSprop 的工作原理

3.1 核心思想

RMSprop 通过对历史梯度的平方进行指数移动平均，自动调节每个参数的学习率：

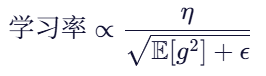
其中：

$( g )$ 是当前梯度；
$( \mathbb{E}[g^2] )$ 是梯度平方的滑动平均；
$( \eta )$ 是初始学习率；
$( \epsilon )$ 是一个小常数（如 $( 10^{-8} )$ ），防止除零。

3.2 算法步骤

设第 $( t )$ 步的梯度为 $( g_t )$ ，则 RMSprop 更新规则如下：

计算梯度平方的滑动平均： $s_t = \beta \cdot s_{t-1} + (1 - \beta) \cdot g_t^2$ 其中 $( \beta )$ 通常取 0.9，表示对过去梯度的记忆权重。
计算调整后的学习率： $\hat{s}_t = \sqrt{s_t + \epsilon}$
更新参数： $w_t = w_{t-1} - \frac{\eta}{\hat{s}_t} \cdot g_t$

✅ 四、几何解释与直观理解

4.1 问题场景

考虑一个椭圆形损失函数，其等高线呈拉长形状：

在长轴方向（梯度小）→ 需要更大的步长才能下降；
在短轴方向（梯度大）→ 需要更小的步长避免震荡。

4.2 RMSprop 的作用

自动放大长轴方向的学习率（因梯度小， $( s_t )$ 小 → 分母小 → 学习率大）；
自动缩小短轴方向的学习率（因梯度大， $( s_t )$ 大 → 分母大 → 学习率小）；

✅ 结果：参数在各个方向上以相似速度下降，实现平滑、高效收敛。

✅ 五、RMSprop 与 SGD 的对比

特性	SGD	RMSprop
学习率	固定	自适应（每参数不同）
梯度敏感性	对大梯度方向更新过快	平衡各方向更新速度
收敛速度	慢，尤其在非各向同性空间	快，尤其适合稀疏数据
内存占用	低	中等（需存储 $( s_t )$ ）
适用场景	简单任务、小数据	深度网络、图像、NLP

✅ 六、实际应用中的注意事项

6.1 参数设置建议

初始学习率 $( \eta )$ ：通常取 0.001 ~ 0.01；
动量系数 $( \beta )$ ：默认 0.9；
$( \epsilon )$ ：默认 ( 1e-8 )；

6.2 与 Adam 的关系

RMSprop 是 Adam 的前身之一；
Adam = RMSprop + 动量（Momentum）；
所以 RMSprop 更适合没有动量需求的任务。

✅ 七、代码示例（PyTorch）

import torch
import torch.nn as nn
import torch.optim as optimmodel = nn.Linear(10, 1)
optimizer = optim.RMSprop(model.parameters(), lr=0.001, alpha=0.9, eps=1e-8)for epoch in range(num_epochs):for batch_x, batch_y in dataloader:optimizer.zero_grad()loss = criterion(model(batch_x), batch_y)loss.backward()optimizer.step()