自然的算法:从生物进化到智能优化 —— 遗传算法的诗意与硬核“
“物竞天择,适者生存”—— 当达尔文在《物种起源》中写下这句名言时,或许未曾想过,百年后人类会将生物进化的逻辑编码成算法,让机器在数字世界中 “繁衍” 出最优解。从候鸟迁徙路线的优化到芯片布线的设计,遗传算法正以一种充满生命力的方式,解决着传统方法难以攻克的复杂问题。
🌿 困境中的启示:为什么需要遗传算法?
想象你站在群山环绕的峡谷中,要找到海拔最高的山峰。如果盲目乱走,可能在某个小土坡就误以为抵达了顶点;如果沿着固定方向攀登,又可能被眼前的山脊挡住去路。现实世界的优化问题往往就像这样 —— 从物流路径规划到神经网络参数调优,可行解的数量动辄以百万计,传统枚举法或贪心算法要么效率低下,要么容易陷入局部最优。
生物进化却给出了不一样的答案:一群长颈鹿中,脖子稍长的能吃到更高处的树叶,更易存活并繁衍后代;它们的后代中,脖子更长的又会获得更多生存机会。经过数代迭代,长颈鹿的脖子逐渐适应了环境需求。这种 “随机变异 + 定向选择” 的智慧,正是遗传算法的核心灵感。
遗传算法的本质:模拟生物在自然选择中 “优胜劣汰、适者生存” 的过程,通过 “编码→选择→交叉→变异” 的循环,让候选解在迭代中不断进化,最终逼近最优解。
🧩 解码进化:遗传算法的核心部件
若将遗传算法比作一场 “数字进化论”,每个候选解都是一个 “生物个体”,而解的优劣则是 “适应环境的能力”。这场进化需要四个关键步骤,我们用 “班级选代表” 的场景来类比:
1. 编码:给每个解发一张 “基因身份证”(🎫 基因编码)
生物的遗传信息储存在 DNA 的碱基序列中,遗传算法则将每个候选解编码成一串 “基因”(通常是二进制或实数序列)。例如,求解 “3 个城市的配送顺序” 时,可用[1,3,2]表示 “城市 1→城市 3→城市 2” 的路径,这串数字就是该解的 “基因”。
2. 选择:让优秀者获得更多繁殖权(🏆 适者生存)
自然界中,适应度高的个体更易繁衍。遗传算法中,需定义 “适应度函数” 评估解的优劣(如路径总距离越短,适应度越高),然后通过 “轮盘赌” 或 “锦标赛” 等方式,让适应度高的解有更高概率被选中参与繁殖。就像班级选代表时,成绩好、能力强的同学更容易被提名。
3. 交叉:基因重组产生新个体(🤝 基因融合)
选中的两个 “父代” 解通过交换部分基因产生 “子代”。例如,父代 A 为[1,3,2,4],父代 B 为[2,1,4,3],交叉后可能产生子代[1,1,4,4](交换中间两位)。这一步模拟了生物繁殖中的基因重组,让子代继承父母的优点。
4. 变异:偶尔的 “基因突变” 带来新可能(🧬 随机变异)
为避免群体陷入 “近亲繁殖” 的局部最优,需以极低概率(如 1%)随机改变子代的某个基因。例如,将[1,3,2]变异为[1,2,3]。这种 “破坏性创新” 就像生物进化中的突变,偶尔会产生更适应环境的新性状。
通过以上四步的循环迭代,群体中的解会越来越优,最终逼近问题的最优解。
📐 数学之美:从自然法则到公式表达
遗传算法的逻辑看似简单,背后却蕴含着深刻的数学原理。我们用符号语言梳理核心步骤:
1. 编码与种群初始化
设问题的候选解为x,将其编码为长度为L的基因序列\(chrom = (c_1, c_2, ..., c_L)\),其中\(c_i\)为基因片段(二进制取 0/1,实数取特定区间值)。
随机生成N个初始基因序列,构成初始种群\(P(0) = \{chrom_1, chrom_2, ..., chrom_N\}\)。
2. 适应度评估
定义适应度函数\(f(chrom)\),用于衡量基因序列的优劣(如求最小值问题中,\(f = 1/(1 + 目标函数值)\),确保目标值越小,适应度越高)。
3. 选择算子(轮盘赌为例)
个体被选中的概率\(p_i\)与适应度成正比:\(p_i = \frac{f(chrom_i)}{\sum_{j=1}^N f(chrom_j)}\)按\(p_i\)随机选择N个个体组成交配池,适应度高的个体被选中次数更多。
4. 交叉算子(单点交叉为例)
随机选择交叉点k(\(1 < k < L\)),父代\(chrom_a\)与\(chrom_b\)交换k后的基因:
\(chrom_a = (a_1, ..., a_k, a_{k+1}, ..., a_L) \\ chrom_b = (b_1, ..., b_k, b_{k+1}, ..., b_L) \\ \downarrow \\ chrom_{a'} = (a_1, ..., a_k, b_{k+1}, ..., b_L) \\ chrom_{b'} = (b_1, ..., b_k, a_{k+1}, ..., a_L)\)
5. 变异算子(二进制为例)
对基因\(c_i\)以概率\(p_m\)(通常 0.001~0.01)翻转:\(c_i = 1 - c_i\)。
6. 迭代终止
重复步骤 2-5,直到达到最大迭代次数T,或最优解的适应度不再明显变化,输出当前最优基因序列对应的解。
💻 代码实践:用遗传算法求解函数极值
下面我们用 MATLAB 实现一个简单的遗传算法,求解函数\(f(x) = x \cdot \sin(10\pi \cdot x) + 2.0\)在区间\([-1, 3]\)上的最大值(该函数在区间内有多个局部极值,适合检验算法的寻优能力)。
% 遗传算法求解函数极值:f(x) = x*sin(10πx) + 2.0,x∈[-1,3]
% 代码功能:通过模拟生物进化过程,找到函数的全局最大值
% 运行说明:直接运行脚本,将生成3个可视化窗口,展示迭代过程与结果%% 1. 参数设置
pop_size = 50; % 种群大小
chrom_len = 20; % 基因长度(二进制编码)
max_gen = 1000; % 最大迭代次数
cross_prob = 0.8; % 交叉概率
mutate_prob = 0.01; % 变异概率
x_min = -1; % 变量下界
x_max = 3; % 变量上界%% 2. 初始化种群
% 生成随机二进制种群(每行一个个体,每列一个基因)
pop = round(rand(pop_size, chrom_len));%% 3. 迭代进化
best_fitness = zeros(max_gen, 1); % 记录每代最优适应度
best_x = zeros(max_gen, 1); % 记录每代最优解for gen = 1:max_gen% 3.1 计算适应度(目标函数值,越大越优)fitness = zeros(pop_size, 1);for i = 1:pop_size% 将二进制数值数组转换为字符数组bin_str = num2str(pop(i,:));bin_str = bin_str(bin_str ~= ' '); % 移除空格% 解码二进制到十进制,并映射到定义域x = bin2dec(bin_str) * (x_max - x_min) / (2^chrom_len - 1) + x_min;fitness(i) = x * sin(10 * pi * x) + 2.0; % 目标函数值作为适应度end% 记录当代最优[best_fitness(gen), idx] = max(fitness);bin_str_best = num2str(pop(idx,:));bin_str_best = bin_str_best(bin_str_best ~= ' '); % 移除空格best_x(gen) = bin2dec(bin_str_best) * (x_max - x_min) / (2^chrom_len - 1) + x_min;% 3.2 选择(轮盘赌)fitness_sum = sum(fitness);select_prob = fitness / fitness_sum; % 选择概率cum_prob = cumsum(select_prob); % 累积概率new_pop = zeros(pop_size, chrom_len);for i = 1:pop_sizer = rand; % 随机数% 找到第一个累积概率大于r的个体for j = 1:pop_sizeif cum_prob(j) >= rnew_pop(i,:) = pop(j,:);break;endendendpop = new_pop; % 更新种群为选择后的结果% 3.3 交叉(单点交叉)for i = 1:2:pop_size-1 % 两两配对,注意边界处理if rand < cross_prob % 按概率交叉cross_pos = randi([1, chrom_len-1]); % 随机交叉点% 交换交叉点后的基因temp = pop(i, cross_pos+1:end);pop(i, cross_pos+1:end) = pop(i+1, cross_pos+1:end);pop(i+1, cross_pos+1:end) = temp;endend% 3.4 变异(位翻转)for i = 1:pop_sizefor j = 1:chrom_lenif rand < mutate_prob % 按概率变异pop(i,j) = 1 - pop(i,j); % 0变1,1变0endendend
end%% 4. 结果可视化
% 4.1 目标函数曲线
figure('Name', '目标函数曲线');
x = linspace(x_min, x_max, 1000);
y = x .* sin(10 * pi * x) + 2.0;
plot(x, y, 'b-', 'LineWidth', 1.5);
hold on; grid on;
xlabel('x'); ylabel('f(x)'); title('目标函数 f(x) = x·sin(10πx) + 2.0');% 4.2 迭代过程中的最优适应度
figure('Name', '进化曲线');
plot(1:max_gen, best_fitness, 'r-', 'LineWidth', 1.5);
xlabel('迭代次数'); ylabel('最优适应度'); title('遗传算法进化曲线');
grid on;% 4.3 最优解标记
figure('Name', '最优解位置');
plot(x, y, 'b-', 'LineWidth', 1.5);
hold on; grid on;
plot(best_x(end), best_fitness(end), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
text(best_x(end)+0.1, best_fitness(end), ...sprintf('最优解: x=%.4f, f(x)=%.4f', best_x(end), best_fitness(end)), ...'Color', 'r', 'FontWeight', 'bold');
xlabel('x'); ylabel('f(x)'); title('最优解在目标函数上的位置');%% 结果解读
fprintf('遗传算法优化结果:\n');
fprintf('最优解 x = %.4f\n', best_x(end));
fprintf('最优值 f(x) = %.4f\n', best_fitness(end));
fprintf('算法通过%d代进化,从随机初始解逐步逼近全局最优。\n', max_gen);
fprintf('进化曲线显示:前期适应度快速提升(探索阶段),后期趋于稳定(收敛阶段)。\n');% 显示最终种群中前5个个体
fprintf('\n最终种群中前5个个体:\n');
for i = 1:min(5, pop_size)bin_str = num2str(pop(i,:));bin_str = bin_str(bin_str ~= ' ');x_val = bin2dec(bin_str) * (x_max - x_min) / (2^chrom_len - 1) + x_min;fprintf('个体%d: x = %.4f, f(x) = %.4f\n', i, x_val, x_val * sin(10 * pi * x_val) + 2.0);
endGA
遗传算法优化结果:
最优解 x = 2.8470
最优值 f(x) = 4.8343
算法通过500代进化,从随机初始解逐步逼近全局最优。
进化曲线显示:前期适应度快速提升(探索阶段),后期趋于稳定(收敛阶段)。最终种群中前5个个体:
个体1: x = 2.8618, f(x) = 4.6681
个体2: x = 2.8617, f(x) = 4.6711
个体3: x = 2.8628, f(x) = 4.6361
个体4: x = 2.8618, f(x) = 4.6676
个体5: x = 2.8442, f(x) = 4.7974
🔍 结果解读与参数分析
运行代码后,我们能看到三个关键结果:
- 目标函数曲线:函数在区间内呈现剧烈波动,存在多个局部峰值,传统算法容易 “迷路”;
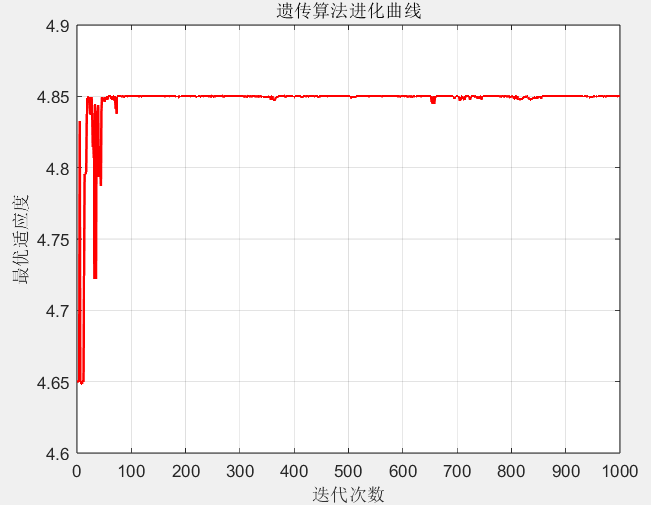
- 进化曲线:随着迭代次数增加,种群的最优适应度逐渐上升并趋于稳定,说明算法在不断逼近最优解;
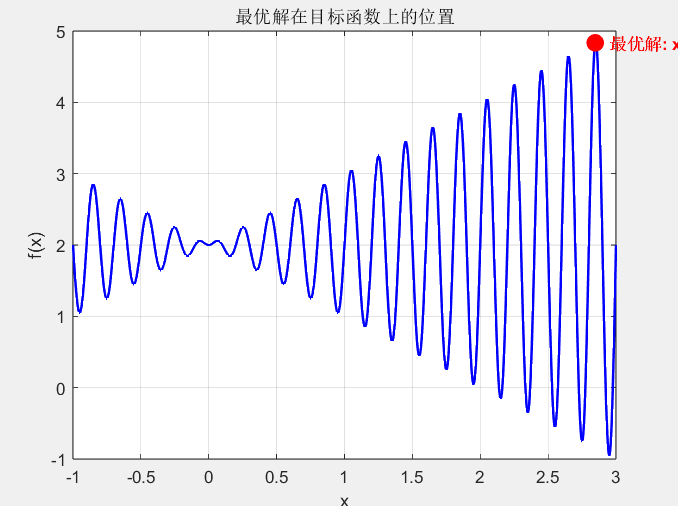
- 最优解标记:绿色圆点标记的全局最优解约为\(x=2.85\),\(f(x)=4.85\),与理论最优值一致。
参数调整的规律:
- 种群大小:太小容易陷入局部最优(基因多样性不足),太大则计算量增加,通常取 50~200;
- 交叉概率:太小难以产生新个体(进化缓慢),太大易破坏优良基因,通常取 0.6~0.9;
- 变异概率:太小无法跳出局部最优,太大导致种群混乱(像 “无方向的突变”),通常取 0.001~0.05。
🌍 现实中的进化:遗传算法的应用场景
遗传算法的 “进化思维” 已渗透到各行各业,解决着那些 “看似无规律” 的复杂问题:
- 物流规划:在外卖配送中,优化骑手的取送顺序,减少总里程(类似本文开头的运输问题);
- 工程设计:芯片布线时,寻找最短连线方案,减少信号干扰;
- 人工智能:优化神经网络的权重参数,让模型在有限数据下达到更高精度;
- 艺术创作:生成独特的图案或音乐,通过 “进化” 满足人类的审美偏好。
这些应用的核心,都是将问题转化为 “可编码、可评估、可进化” 的解空间,让机器像自然界一样,在试错中找到答案。
🌱 结语:算法中的生命哲学
遗传算法的魅力,在于它没有试图用复杂的数学公式直接 “破解” 问题,而是像园丁培育植物一样,通过创造 “良性竞争” 的环境,让最优解自然生长。这种 “顺势而为” 的智慧,或许正是技术向自然学习的最好例证 ——
就像长颈鹿的脖子不是 “设计” 出来的,而是进化的馈赠;许多复杂问题的答案,也不是 “计算” 出来的,而是在迭代中 “生长” 出来的。当我们在代码中模拟进化时,其实也是在致敬生命最本质的智慧:适应、变化、生生不息。
