算法33.0
1314. 矩阵区域和 - 力扣(LeetCode)
自己的理解:
算题的时候 计算二维数组的和的时候 第一反应是按照自己的方式 并没有联想到之前学习过二维前缀和的内容 必要且及时的复习
如何快速的得出二维数组的前缀和公式:
提示:两个图片能否勾起算法27.0 里面的解析
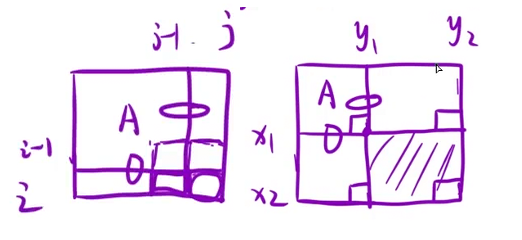
分为如何求 dp[ i ][ j ] 以及如何使用前缀和数组 这两个图片一个对应一个
dp[][]是要注意面积的拆分 使用是要注意明确好区间之后 大面积减去小面积
如何计算answer某一个位置的数?
首先这里的k并不是固定的等于1 所以这个绿框框的范围是根据k的大小而改变的
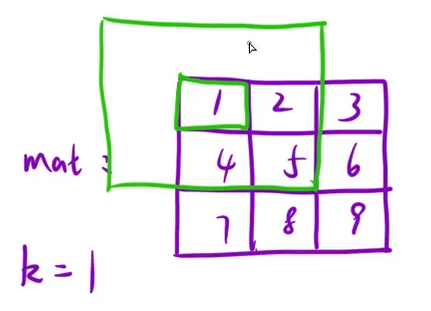
如何确定这个范围呢? 受到使用二维前缀和数组那里的启示 其实是要确定左上角和右下角的坐标 确定好了之后 这个范围就确定了 再把这个范围套到mat(arr)上进行计算
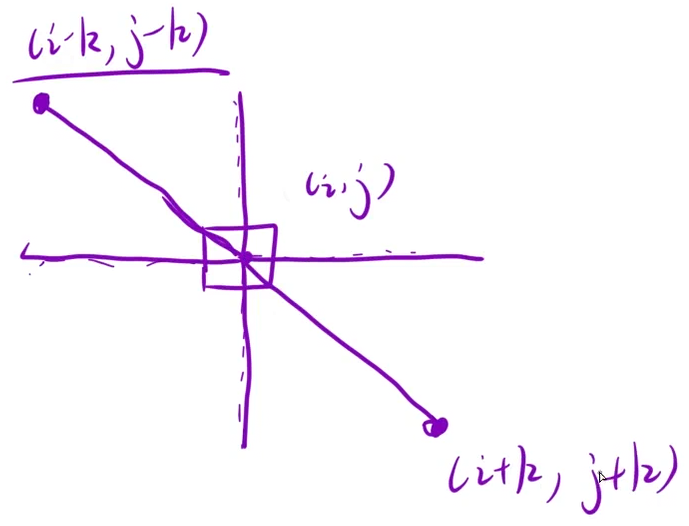
注意数组越界异常 因为这个往mat数组上套的时候 有时候一部分是在外面的 外面的这部分元素不需要也获取不到 还会造成数组越界异常 就像下面的情况(k=1)
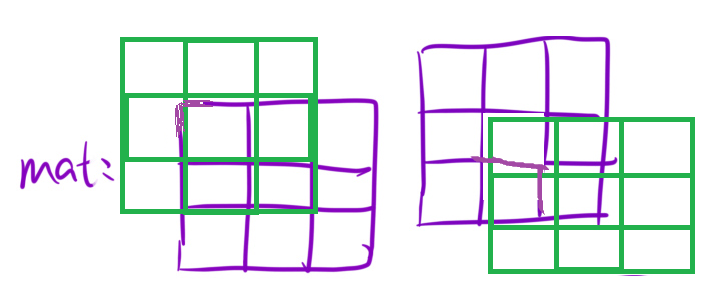
这个时候要怎么解决?
对于左上角方块 我们需要注意的是补药小于0 而对于右下角方块 我们需要注意的是补药超了mat数组本身
我们可以用函数来解决这个问题 取值
小的不可能小过0 大的不可能大过m-1(边界)
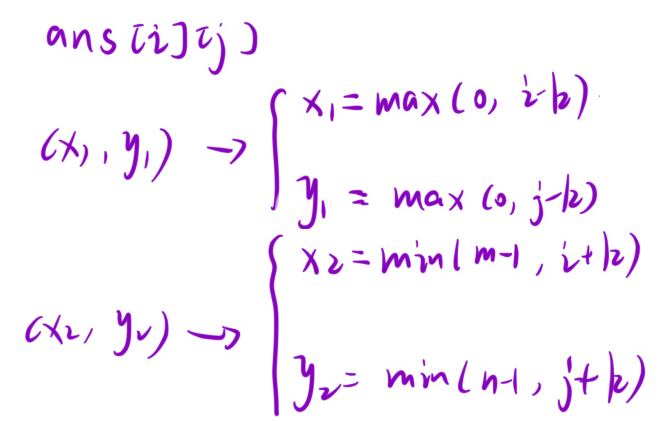
下标的映射关系:?
在之前学习二维前缀和模板的时候 为了避免边界情况的麻烦 我们是默认了dp数组下标从1开始
但是这道题的数组下标是从0开始的 这个时候要怎么解决? 画出来好理解一些:
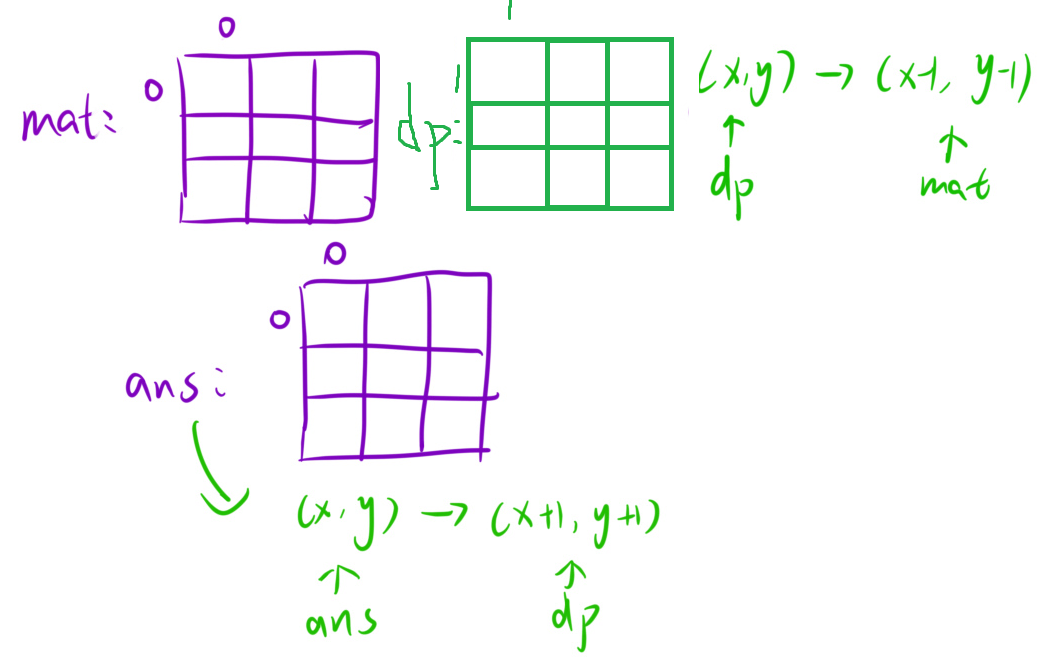
如果这里有点迷糊的话 从算法27.0推导出来的公式入手
D = dp[ x2 ][ y2 ] - dp[ x1-1 ][ y2 ] - dp[ x2 ][ y1-1 ] 如果x1取0的话 是负1 这里需要处理边界情况
之前的话 我们的arr数组从1开始 我们的dp也是从1开始 (但是现在dp是从0开始 扩充了)
填写dp表(1,1)的时候,我们需要在mat表里面找的是(0,0)
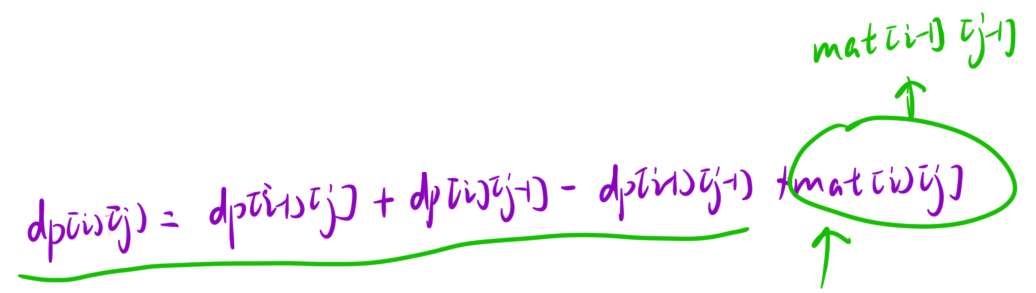
同理 使用dp表的时候 ans也是从0开始计数的 填写ans(0,0)的时候 dp表需要统一加1
 .这样太麻烦了 当用到dpi的时候统一加一减一的
.这样太麻烦了 当用到dpi的时候统一加一减一的
更方便的是 在求下标的时候 直接加1
求answer边界的时候 直接在answer上面加1 对应到dp表里面
解释:想象一下 你有一个正常的世界 和 一个带缓冲区的世界
正常的世界是原矩阵 房子编号从0 开始 0 1 2 3 4 ...
带缓冲的世界是dp表 房子编号从0开始 0(缓冲区) 1 2 3 4 ...
之前我们为了避免边界 规定了0号房子是空的缓冲区 从1号开始才对应正常世界的房子
这样设定之后
在正常的世界中 你想要从2号房子到4号房子的朋友:
正常世界:2号到4号 带缓冲的世界:需要找3号到5号(因为1号对应正常世界的0号)
与其每次都在脑子里面转换:正常世界的2号房子对应缓冲世界的3号 正常世界4号对应缓冲5号
不如统一规则:只要从正常的世界去缓冲世界 所有地址自动+1
放到代码里表现就是:
int x1 = Math.max(0,i-k)+1,y1=Math.max(0,j-k)+1;
int x2 = Math.min(m-1,i+k)+1,y2=Math.min(n-1,j+k)+1;
这样就会简化很多步骤
细节:
审题:这道题目审题比较不容易 其实就是要把握住关键概念 少一点想法多一点现实迭代
本题:answer二维数组和mat二维数组同等规模
这个是审题的关键 : i-k<= r <= i+k j-k <= c <= j+k 带入数字之后-1<= r <= 1 这个 表示的是在mat数组上从-1 到 1 的位置

别人的讲解:
下面是题目、效果图和代码:

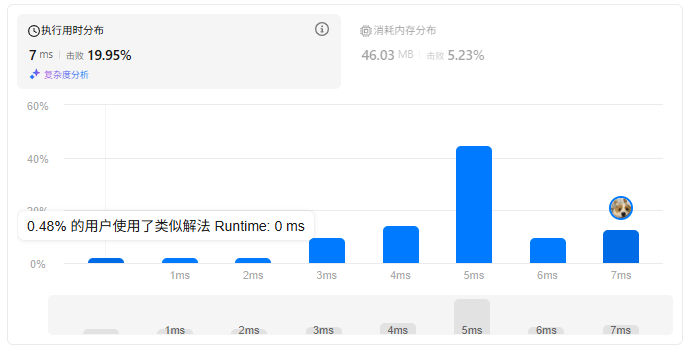
class Solution
{public int[][] matrixBlockSum(int[][] mat, int k) {//先求一下原矩阵的规模int m = mat.length , n = mat[0].length;//1.预处理一个前缀和矩阵int[][] dp = new int[m+1][n+1];for(int i = 1; i<= m; i++ ){for(int j = 1;j<=n ; j++)dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];}//2.使用前缀和矩阵int[][] ret = new int[m][n]; //同等大小就可以for(int i = 0; i<m; i++ )for(int j = 0;j<n ; j++){int x1 = Math.max(0,i-k)+1,y1=Math.max(0,j-k)+1;int x2 = Math.min(m-1,i+k)+1,y2=Math.min(n-1,j+k)+1;ret[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];}return ret; }
}//xiyu251113&1#4*8