计算机视觉11-相机模型与多视几何

2d图像可以看作3d的一个子空间

三维视觉：关注相机的位置姿态，三维场景的重构

MVS = Multi-View Stereo，多视图立体重建

• 输入：多张已知相机位姿的图片（这些位姿通常由 SfM 算出来）。

• 目标：在每一个像素上估计可靠的深度，得到稠密点云/网格模型。

可以这么理解：

• SfM：先用特征点匹配 +几何约束，只重建出稀疏的三维点（角点、特征点）和相机外参。

• MVS：在 SfM 结果的基础上，利用多张图像之间的视差，把“空白区域”也补上，变成稠密三维结构（深度图、稠密点云、三角网格）

PnP = Perspective-n-Point 问题

• 已知：

  • 一些三维点的坐标（世界坐标系里，通常是地图中的点）；

  • 它们在当前图像上的2D 像素位置；

  • 相机内参（焦距、主点等）。

• 求：

  • 当前相机相对于世界坐标系的位姿（R、t）——也就是“在什么位置、朝哪儿看”。

常见变体有 P3P、EPnP 等，通常会配合 RANSAC 使用来去除误匹配点。

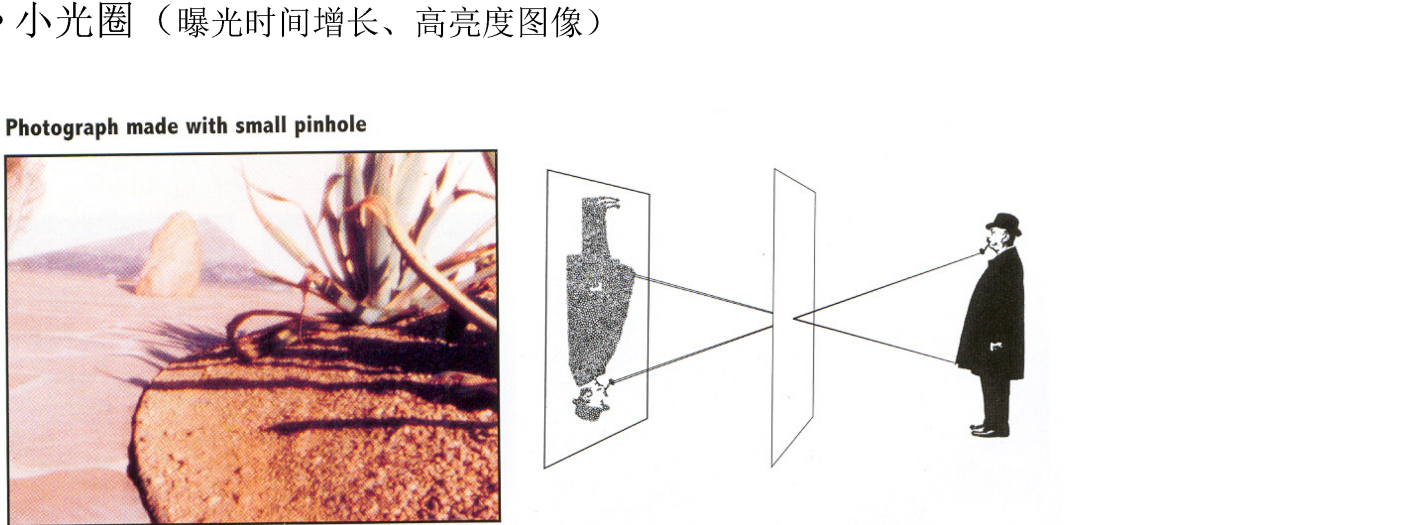
光圈过小可能产生衍射现象

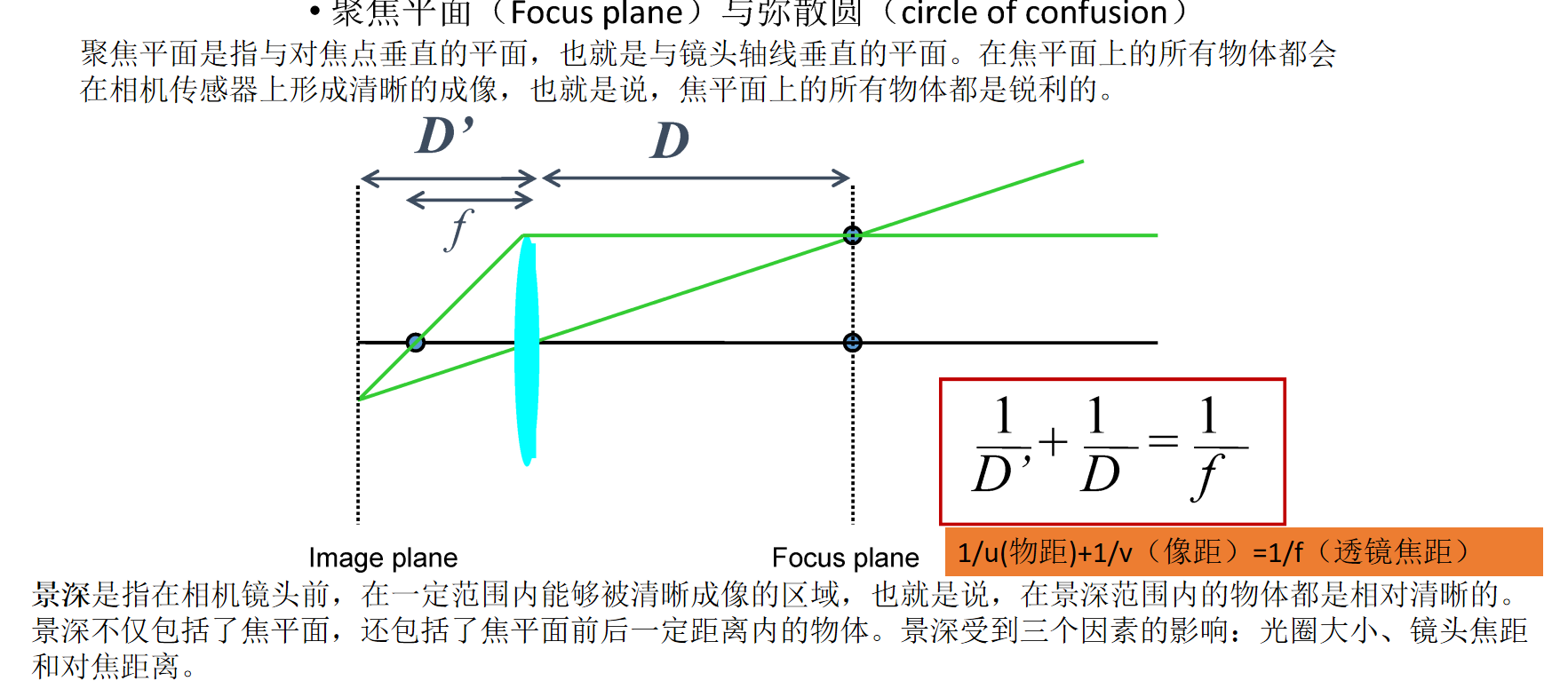
D'为相距，D为物距

公式非常重要！！！

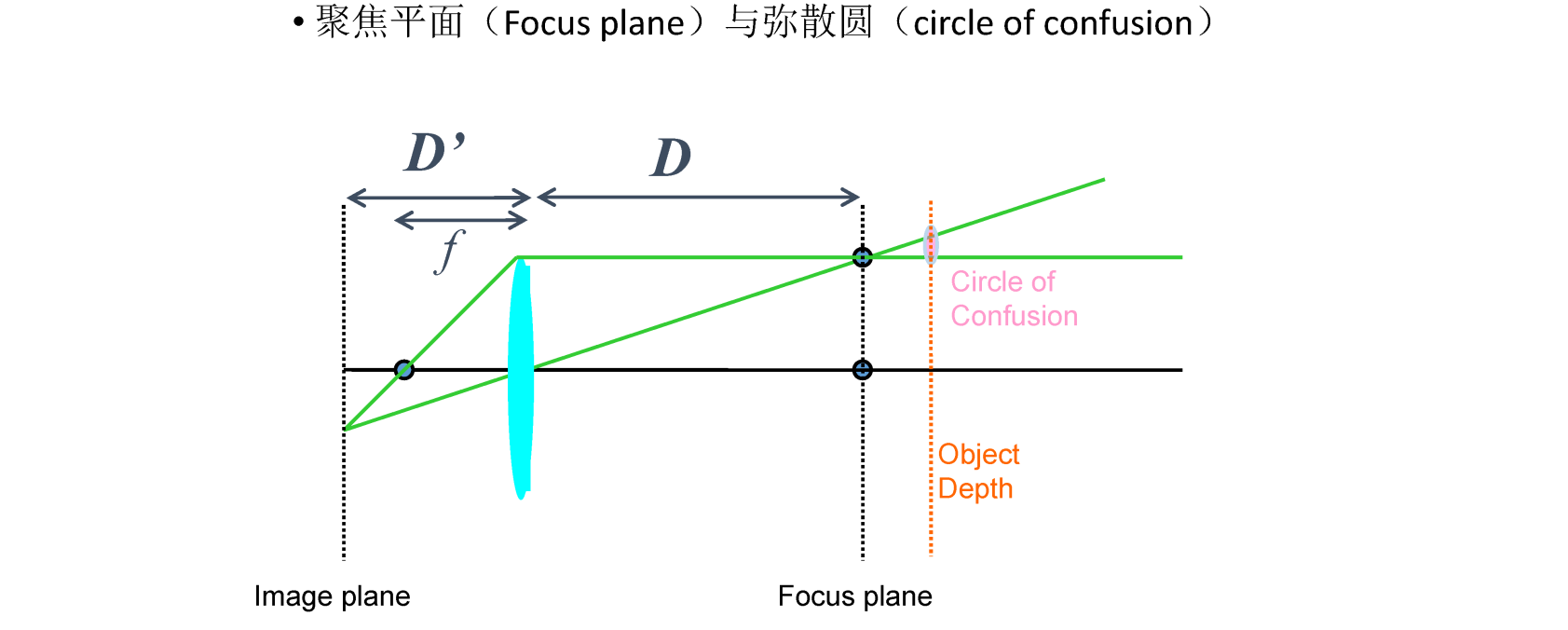
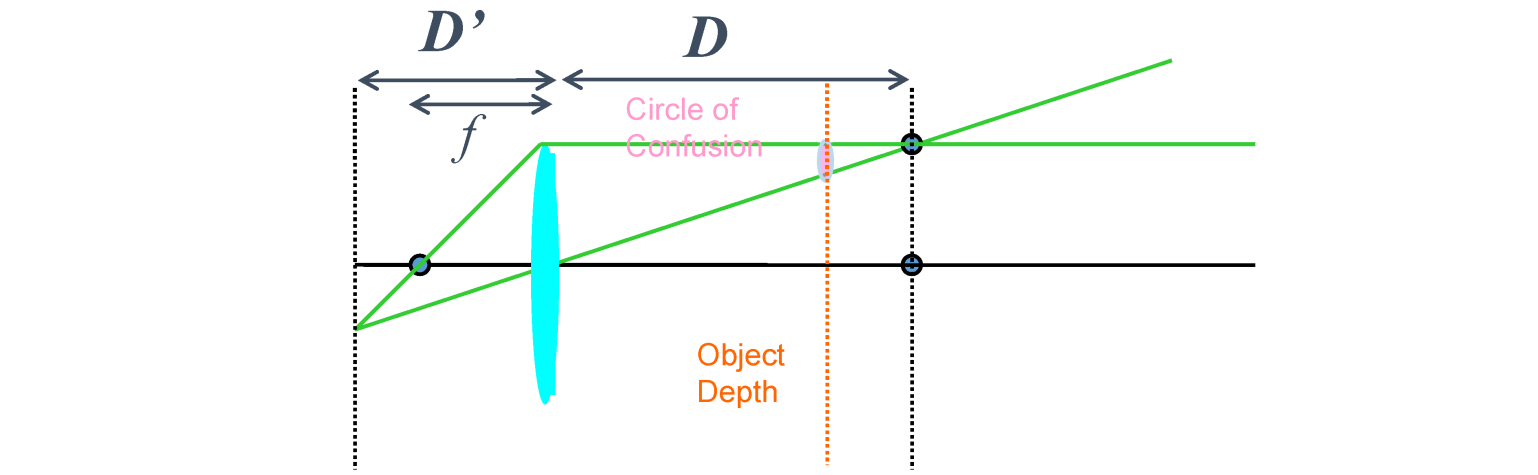
超出景深范围，有弥散圆，太远太近都不行

弥散圆：指的是物点成像时，由于像差，其成像光束不能会聚于一点，在像平面上形成一个扩散的圆形投影。弥散圆在焦点前后，光线开始聚集和扩散，点的影象变成模糊的，形成一个扩大的圆。

景深是个范围，受到光圈等影响

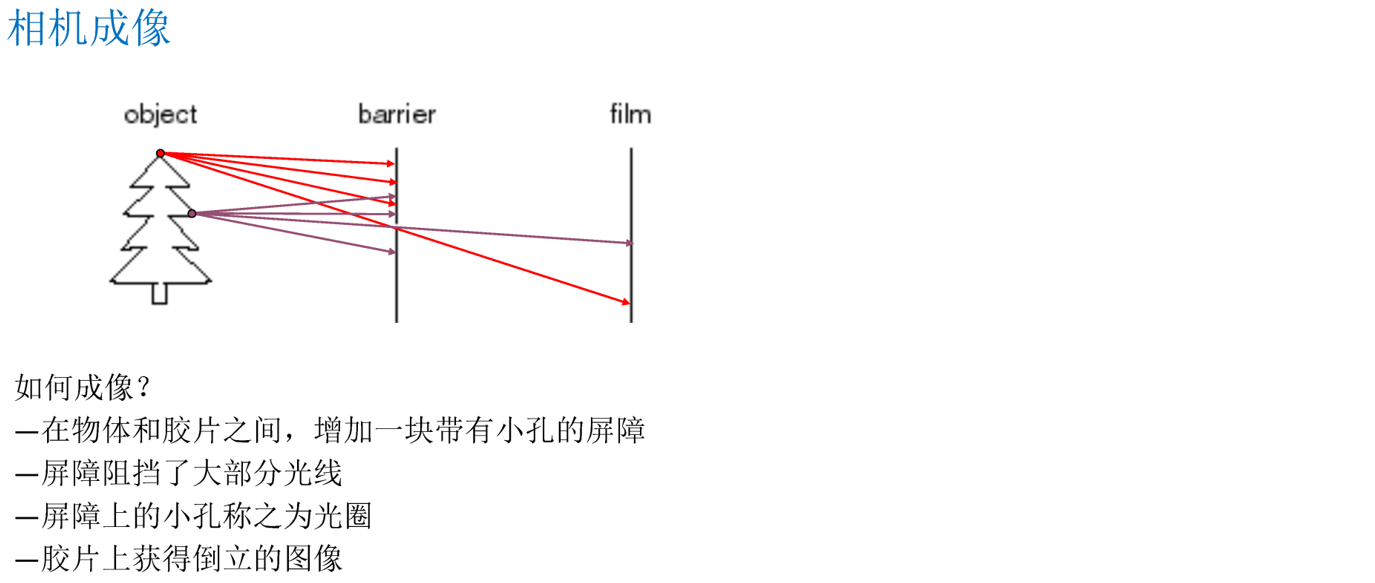
光圈是一个用来控制光线通进入镜头的装置，它通常是在镜头内，对于已经制造好的镜头，我们不可以随意的改变镜头的镜头，但是可以通过在镜头内部加入多边形或者圆形，并且面积可变的孔径光栅来达到控制镜头通光量。

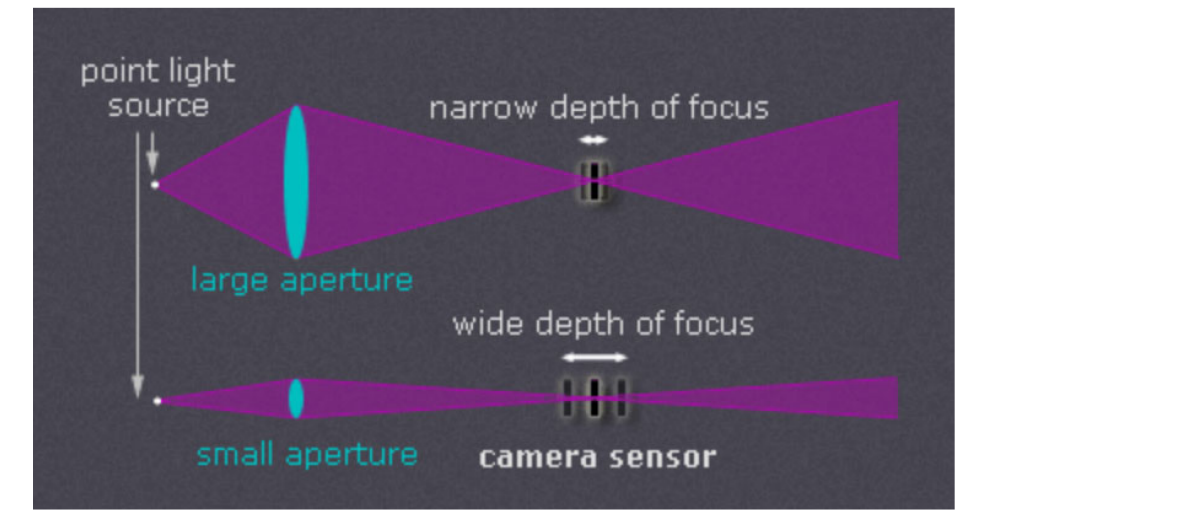
光圈越大景深越浅，光圈越小景深越深

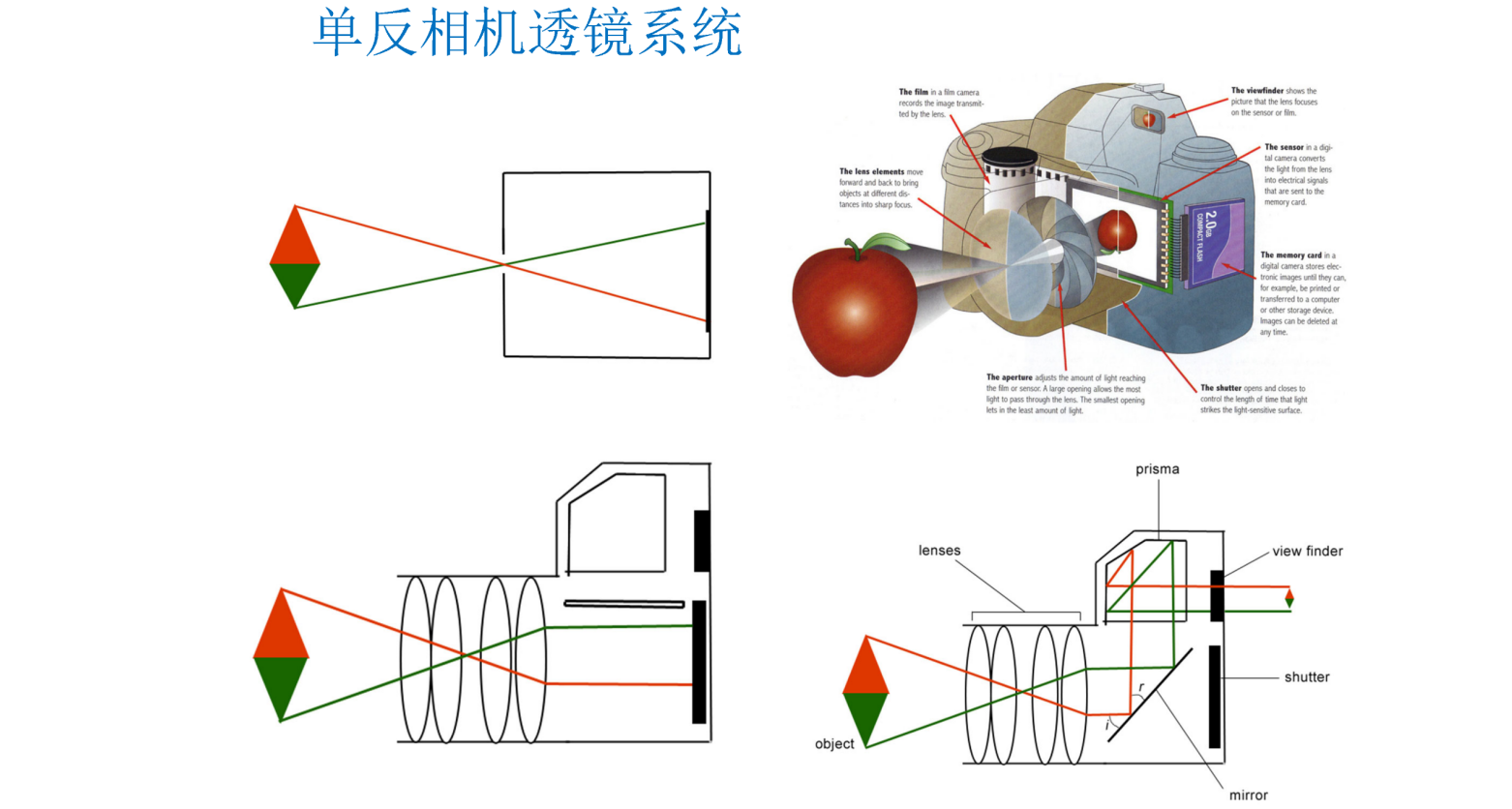
欧式空间到摄影空间的转化，从3d到2d，丢失了一定的信息

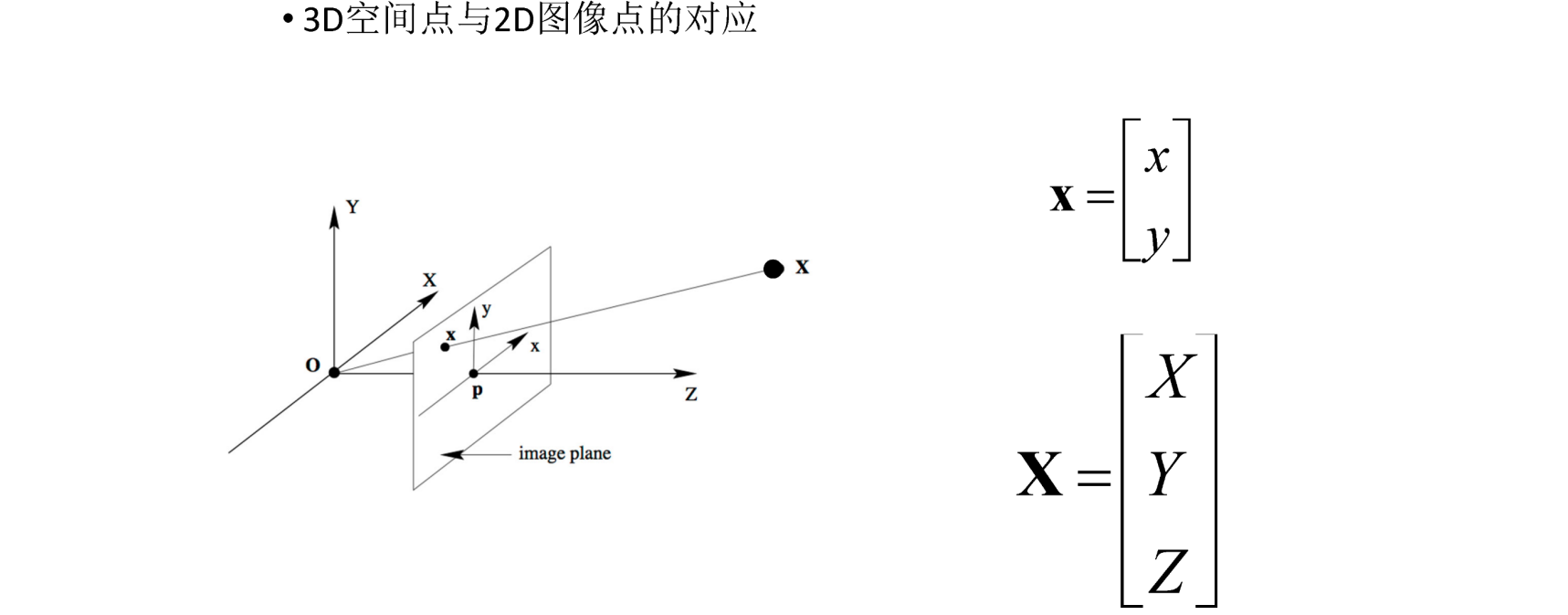
分别建立两个坐标系，图中有一定的约束关系

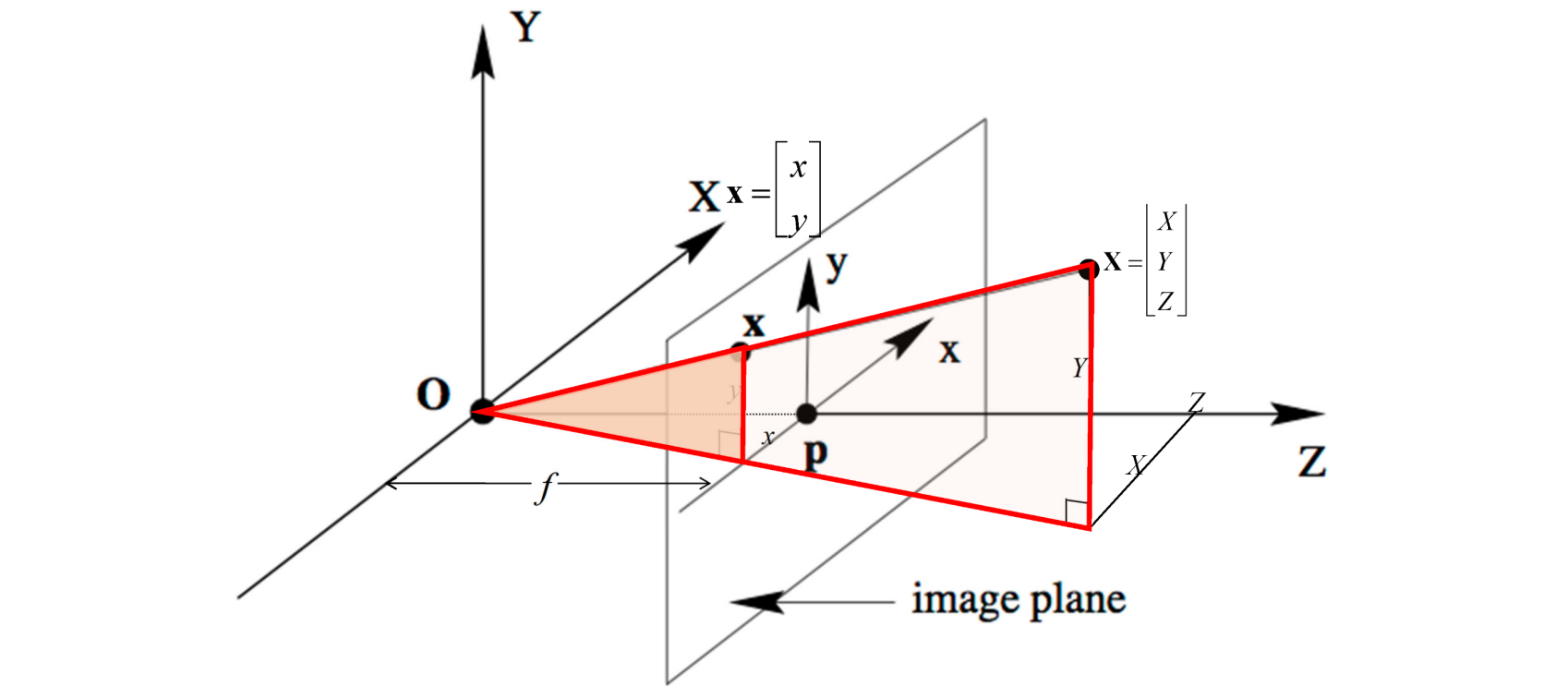
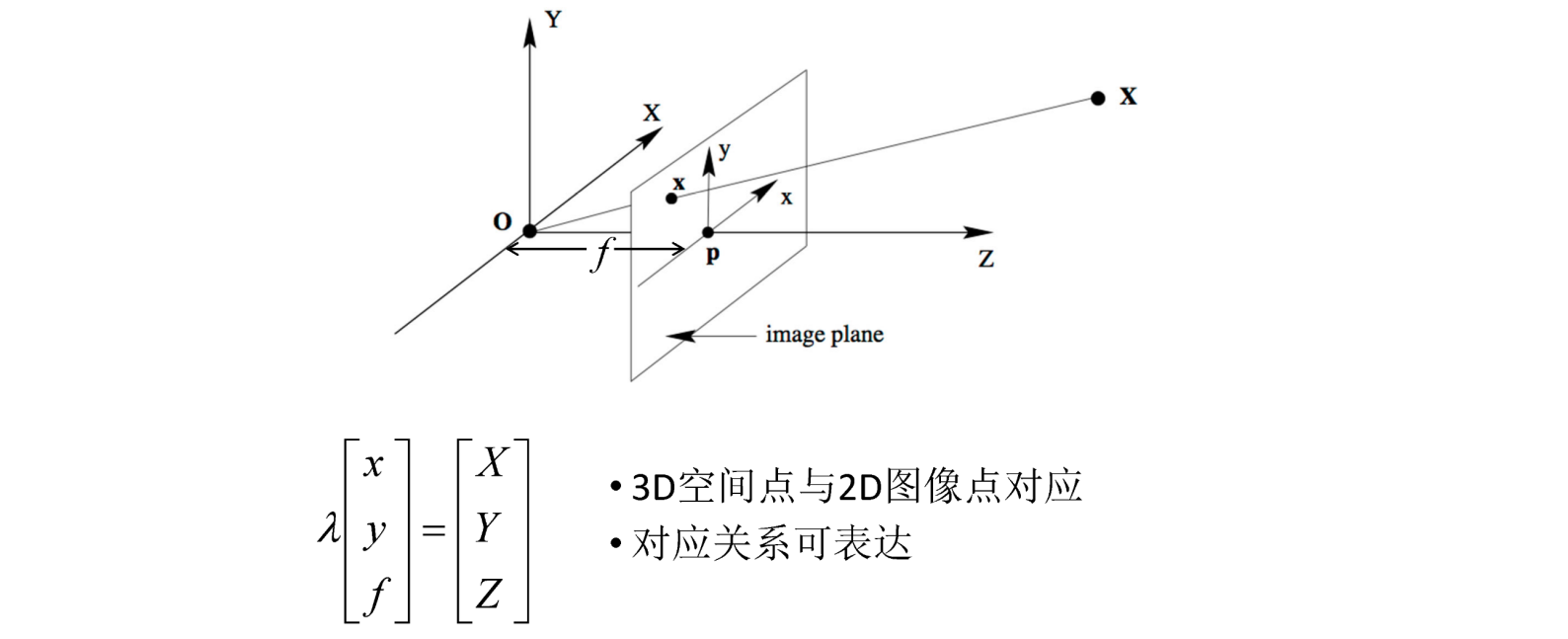
问题

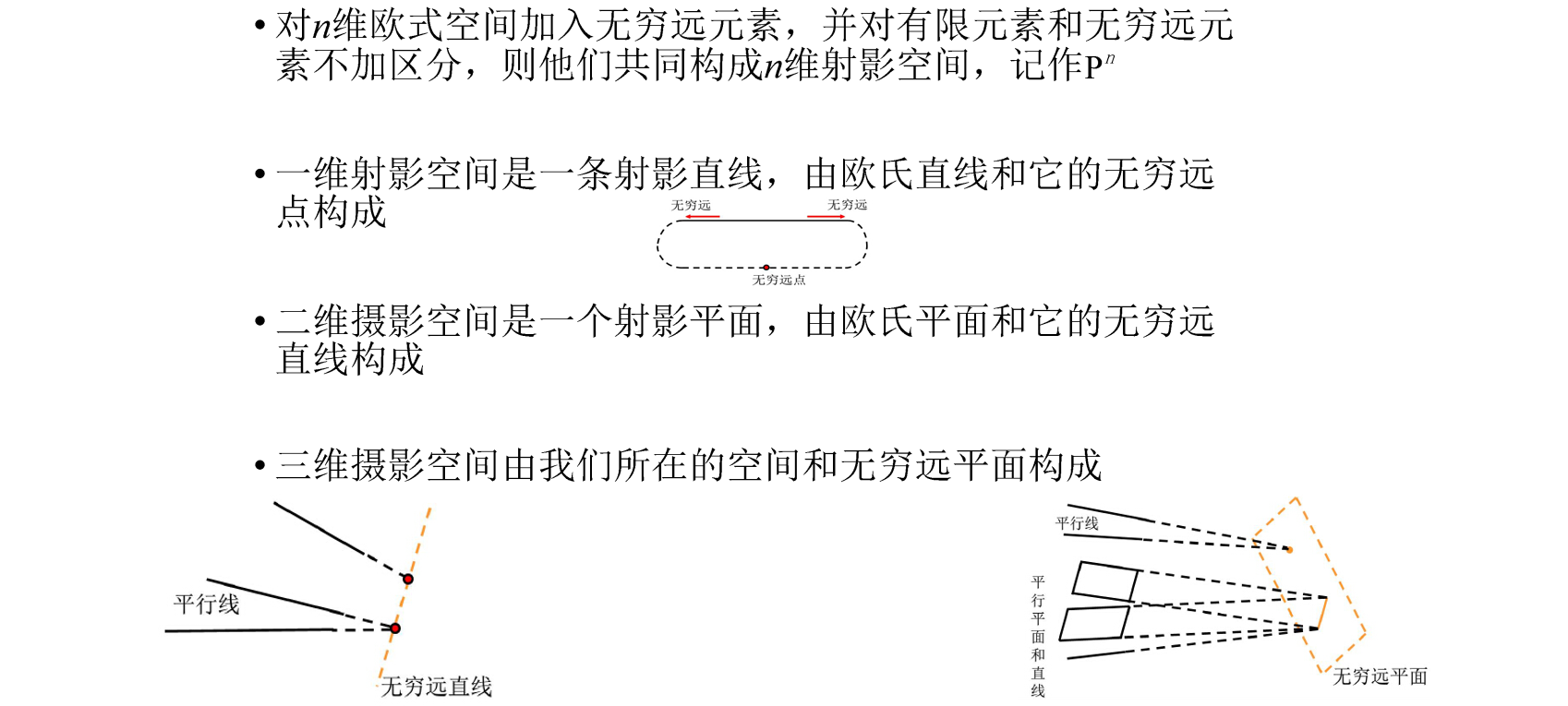
• 在一条直线上只有唯一一个无穷远点
• 在一个平面上，所有的无穷远点组成一条直线，称为该平面的无穷远直线
• 三维空间中的所有无穷远点组成的一个平面，称为这个空间的无穷远平面

再加入齐次坐标（统一维度）

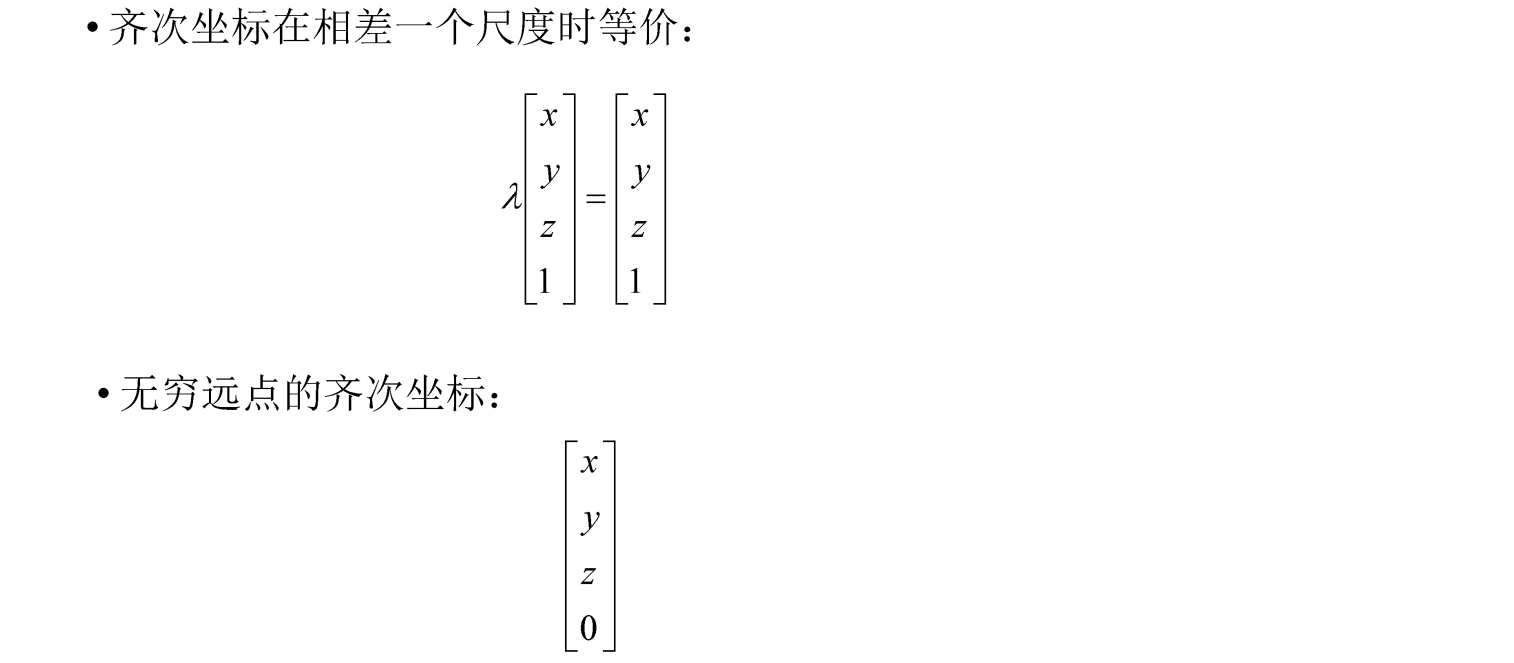
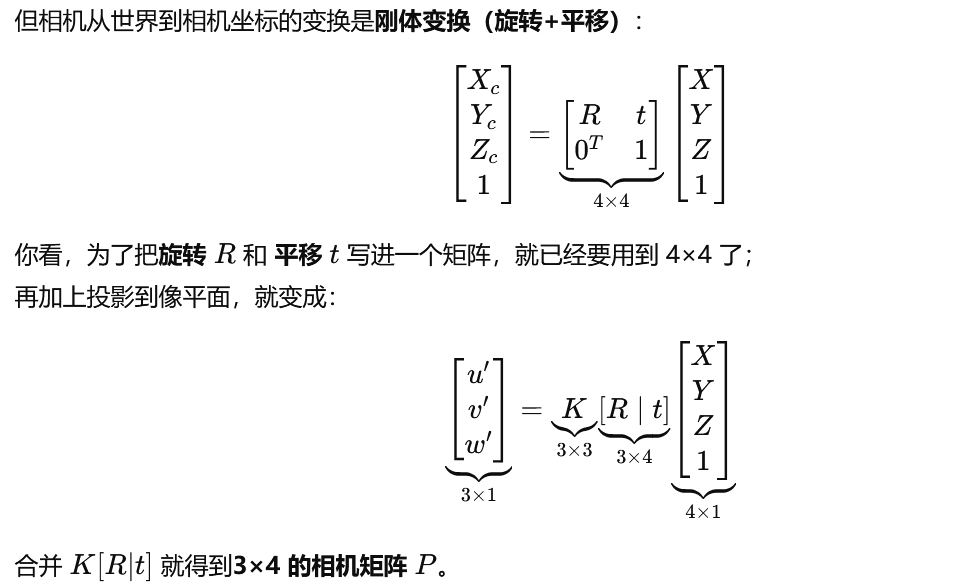
相机模型（重要！！！）

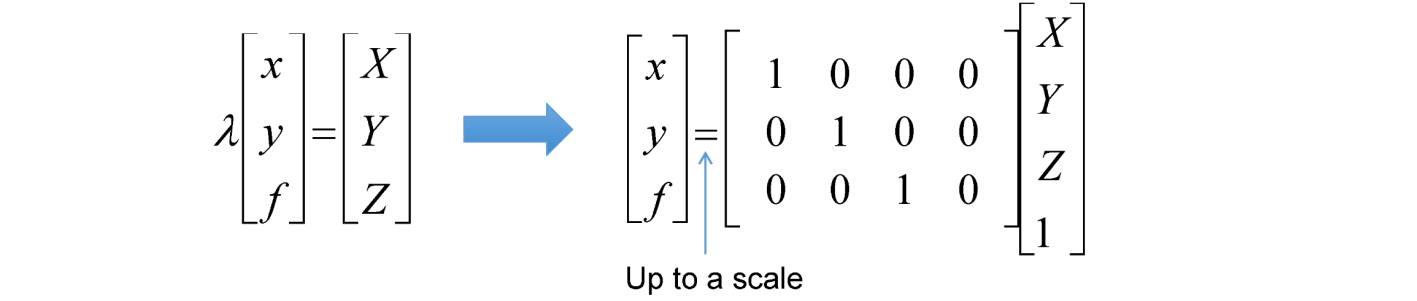
注意：f的单位改为像素

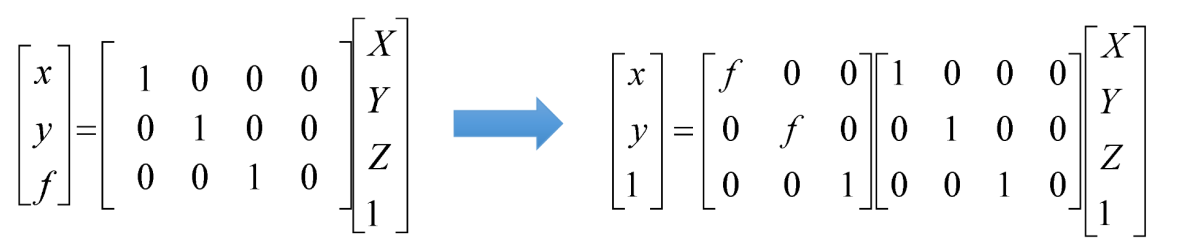
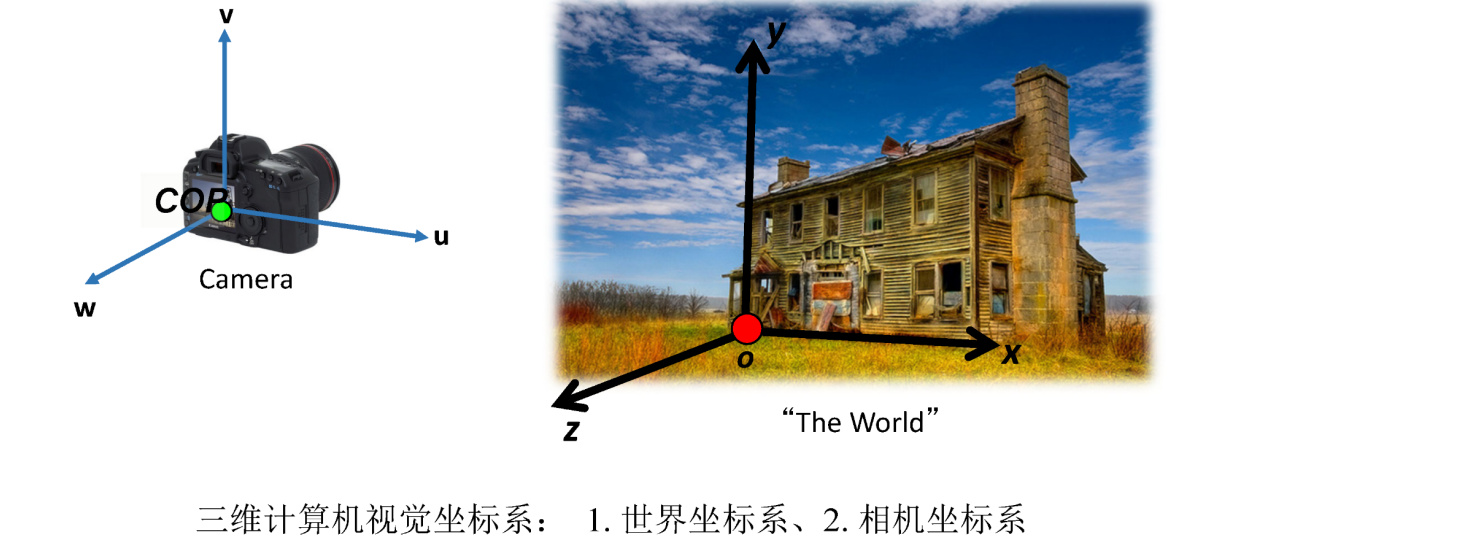
两个坐标系变化只有旋转、平移

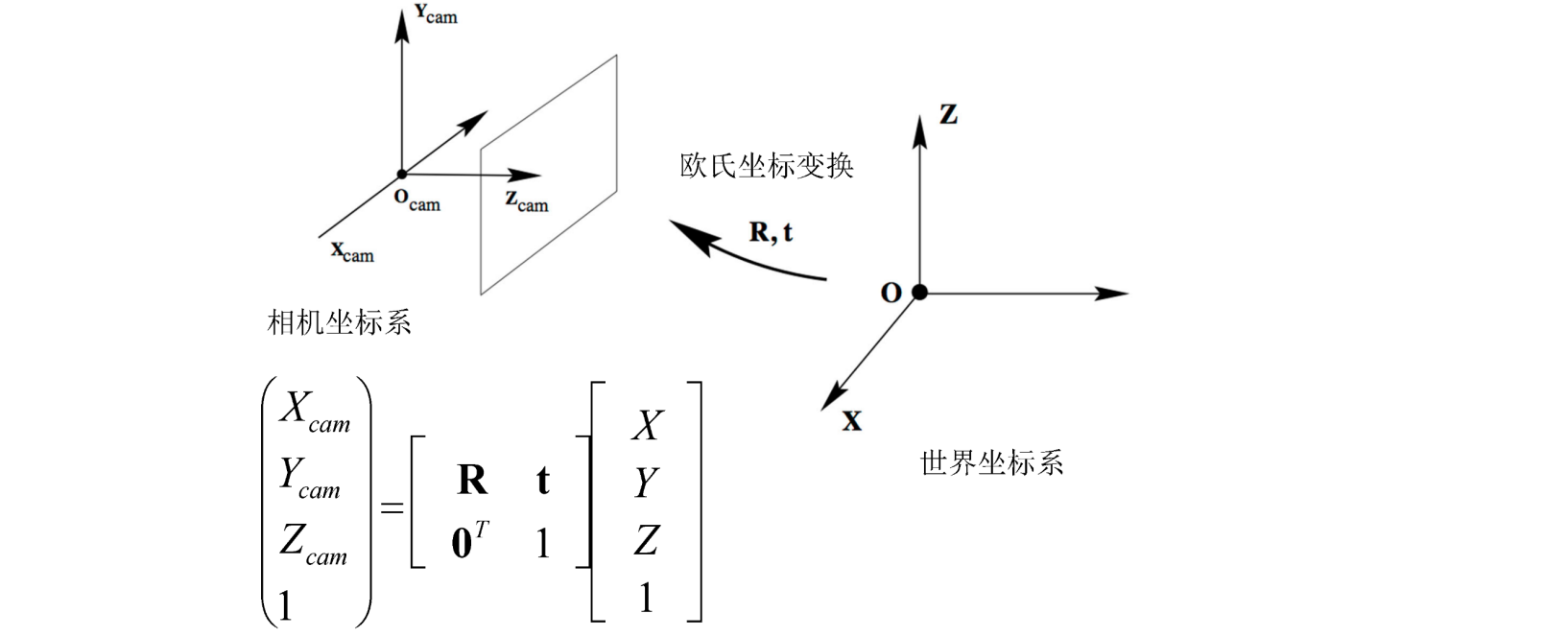
最后得到投影与真实坐标之间的关系

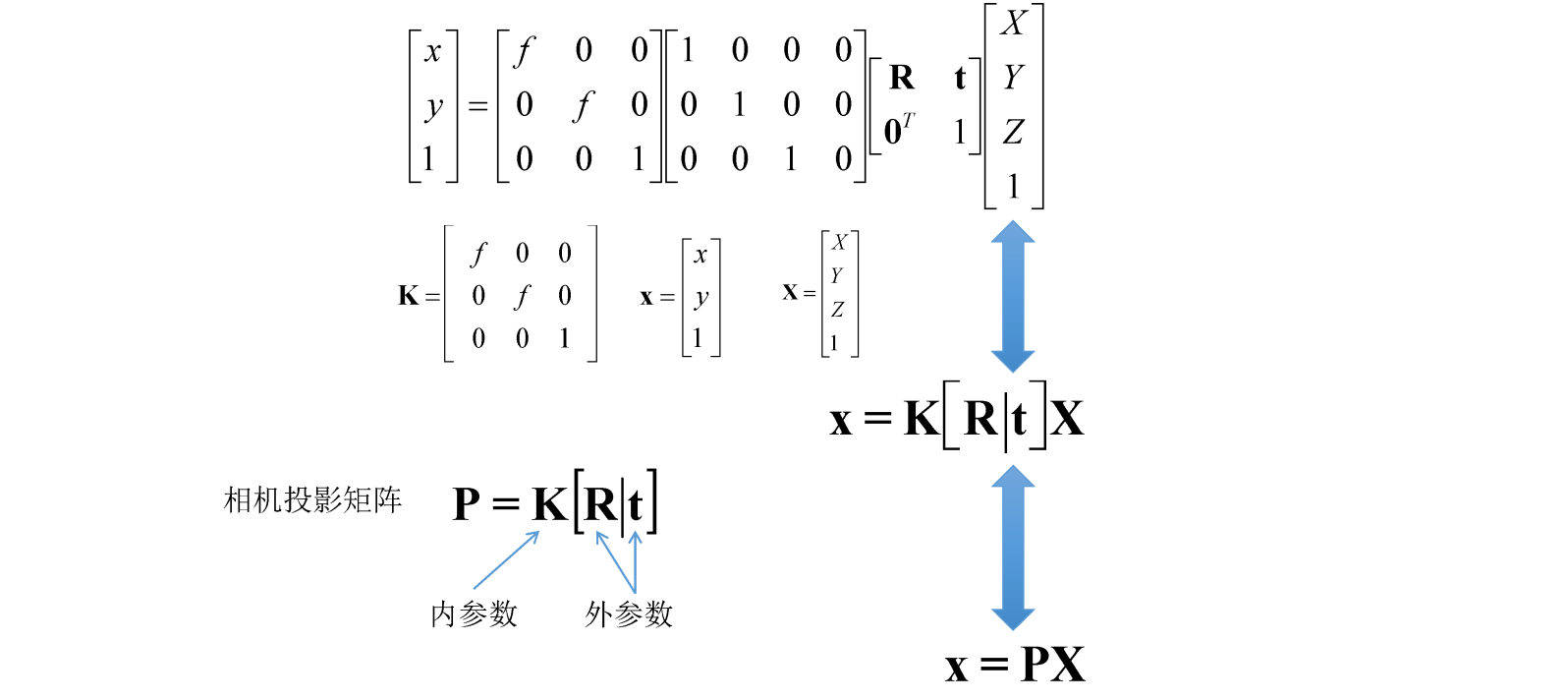
K为焦距的部分

R由于相机的姿态造成的旋转与平移（相对于世界坐标系而言）

公式非常重要！！！

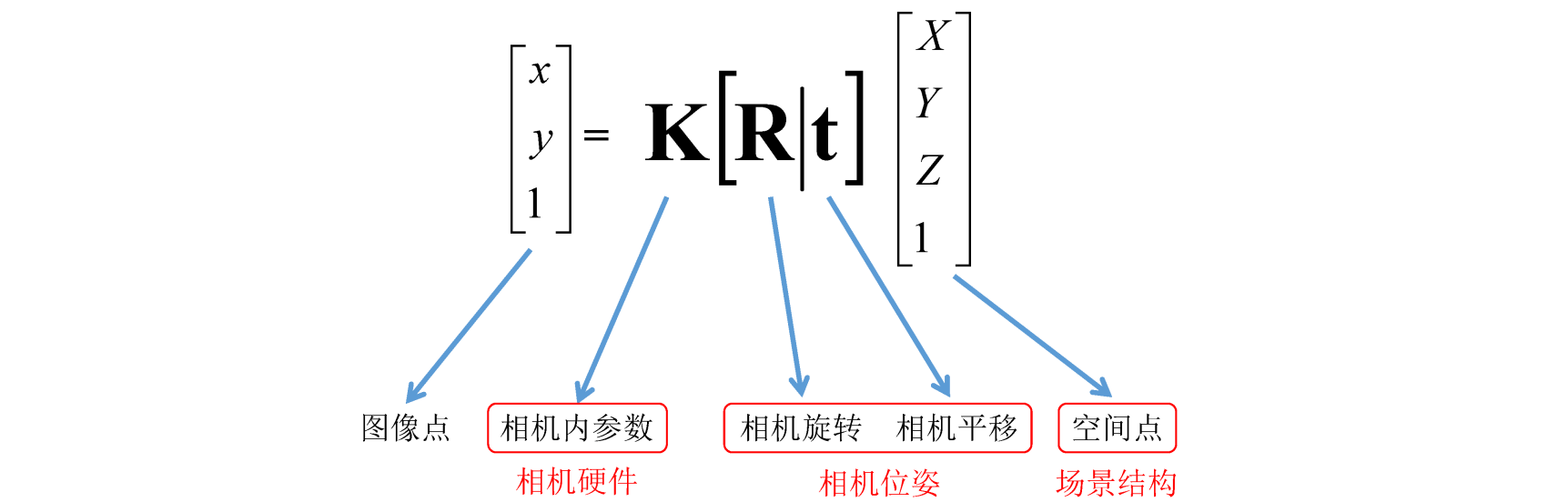
对于矩阵的维度