AtCoder Beginner Contest 431 vp补题

D dp

这题是0-1 背包dp：每个物品只能选一次（要么装头部，要么装身体），且存在 “头部总重量≤总重量的一半” 的容量约束。

struct it{int w,h,b;
};void solve()
{int n;cin>>n;vector<pii>a;int wsm=0,bsm=0;forr(i,1,n){int w,h,b;cin>>w>>h>>b;wsm+=w,bsm+=b;if(h>b)a.push_back({w,h-b});//贪心 h<b的一定放body上 选h>b的放head上}int hw=wsm/2;//头部容量约束vector<int>dp(hw+1,0);//dp[w]=头部重量w时最大价值dp[0]=bsm;for(auto [w,g]:a){reforr(i,1,hw){if(i<w)break;dp[i]=max(dp[i],dp[i-w]+g);}}int mx=0;forr(i,0,hw)mx=max(mx,dp[i]);cout<<mx<<endl;//一开始写的贪心 通不过sample3// vector<it>hm,bm;// int wsm=0,ans=0;// forr(i,1,n){//     int w,h,b;cin>>w>>h>>b;//     wsm+=w;//     if(h>b)hm.push_back({w,h,b});//     else ans+=b;// }// sort(hm.begin(),hm.end(),[&](it x,it y){//     return x.w==y.w?x.h>y.h:x.w<y.w;//以重量为大排序 可能价值大的重量也大 最后可能选不到 无法保证总价值最大// });// int hw=0,id=-1;// // for(auto [w,h,b]:hm)cout<<w<<' '<<h<<endl;cout<<endl;// forr(i,0,hm.size()-1){//     auto [w,h,b]=hm[i];//     if(2*(hw+w)>wsm){//         id=i;//         break;//     }//     hw+=w;//     ans+=h;// }// // cout<<id<<endl;// if(id!=-1){//     forr(i,id,hm.size()-1){//         auto [w,h,b]=hm[i];//         ans+=b;//     }   // }// cout<<ans<<endl;    
}

E 最短路

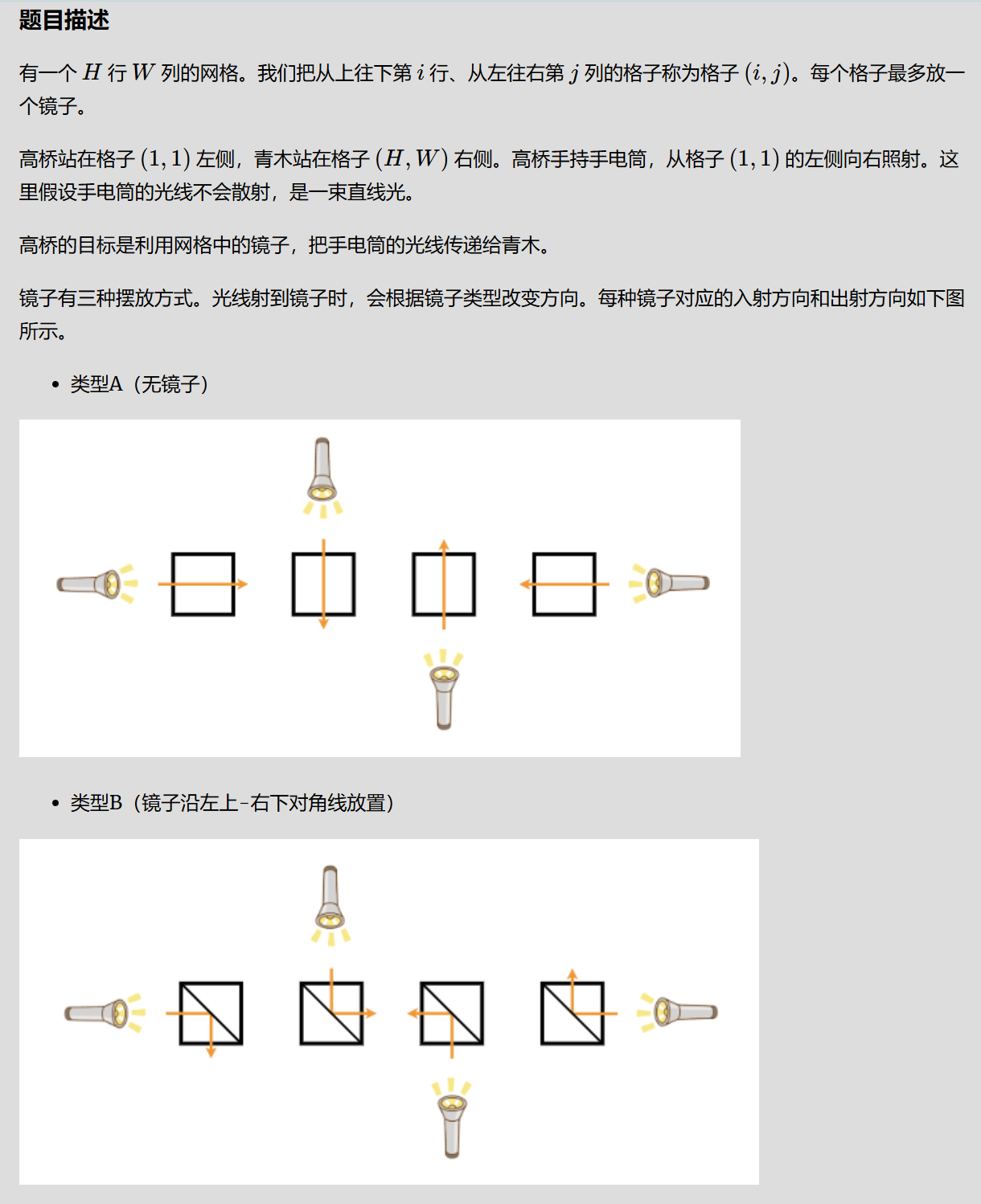
思路来源
大致思路是枚举每个位置的镜子类型，找最短路
一开始在纠结修改会不会对之后的状态有影响的问题

• 假设原始a[x][y]是 ‘A’，当我们尝试用 ‘B’ 时，代价 + 1，这只是 “这一次经过 (x,y) 时选择 B” 的情况
• 未来再次经过 (x,y) 时，仍然可以重新选择 A/B/C（因为允许 “任意修改镜子类型”，每次经过都可以独立选择）
• 而且如果有修改，所记录的一定是只修改到让修改次数最少的那一次

修改次数分析 来源
首先可以讨论证明如果某个单元格必须发生改变，那么这个单元格只会被经过一次：

• 如果某个单元格经过某次修改变成了 A 类型，那么不可能被垂直经过一次再水平经过一次，因为这样的路径交叉不如一开始就让光线在这个单元格内拐弯。
• 反之亦然，如果某个单元格经过某次修改变成了 B / C 类型，假设接下来该单元格被光线经过了两次，那么经过的肯定是该镜面的两侧，这样的路线交叉明显也不如一开始就建成另一种类型的反射镜面，能够直接让光线拐到原本经过两次才能到达的方向上。

经过上述讨论，既然控制了每个位置最多只会改变一次*（一步到位），那就可以放心地把修改产生的影响直接计入搜索状态，而不用担心会影响原本的网格图信息。

看到有位dalao用了01BFS 速学了一下

const int N=5e5+12,inf=1e18;
struct it{int x,y,d;
};
int ex[4]={0,0,1,-1};
int ey[4]={1,-1,0,0};
vector<int>dis[4][N];//记录最短路
string dr="ABC";
void dr_change(char c,int d,int &nx,int &ny,int &nd){int x=ex[d],y=ey[d];switch (c){case 'A':nx=x,ny=y;break;case 'B':nx=y,ny=x;break;default:nx=-y,ny=-x;break;}forr(i,0,3){if(nx==ex[i]&&ny==ey[i]){nd=i;break;}}
}
void solve()
{int h,w;cin>>h>>w;vector<string>a(h+1);forr(i,1,h){cin>>a[i];a[i]=' '+a[i];}forr(di,0,3){forr(i,1,h){dis[di][i].assign(w+2,inf);}}deque<it>q;q.push_front({1,1,0});//还是用标号代替方向简洁一点 若用方向向量会有负的dis[0][1][1]=0;int ans=inf;while (q.size()){// auto [x,y,drx,dry]=q.front();auto [x,y,d]=q.front();q.pop_front();for(auto ndr:dr){int ndis;if(a[x][y]==ndr)ndis=dis[d][x][y];else ndis=dis[d][x][y]+1;int ndx,ndy,nd;dr_change(ndr,d,ndx,ndy,nd);int nx=ndx+x,ny=ndy+y;//下一个位置if(nx==h&&ny==w+1&&ndx==0&&ndy==1)ans=min(ans,ndis);if(nx<1||ny<1||nx>h||ny>w)continue;if(dis[nd][nx][ny]>ndis){dis[nd][nx][ny]=ndis;if(a[x][y]==ndr)q.push_front({nx,ny,nd});else q.push_back({nx,ny,nd});}}}cout<<ans<<endl;
}

F 组合数学

思路来源
要求重排后$a_{i+1}\ge a_i-D$，那么$<a_i-D$的部分($pos$之前)必须在$a_i$前面，$a_i$放在不同$\ge a_i-D$的数之后就能产生不同序列，所以是dalao文章里说的可选位置有$i-pos+1$个
相同的数字作用相同，全都任意放在可选位置的话会形成相同数字的全排列，除掉去重就行

const int N=2e5+12,inf=1e18,mod=998244353;
int fac[N],ifac[N];
int qpow(int a,int b){int res=1;for(;b;(a*=a)%=mod,b>>=1)if(b&1)(res*=a)%=mod;return res;
}
int inv(int x){return qpow(x,mod-2)%mod;}
void init(int n){fac[0]=1;forr(i,1,n)(fac[i]=i*fac[i-1])%=mod;ifac[n]=inv(fac[n]);reforr(i,1,n-1)(ifac[i]=(i+1)*ifac[i+1])%=mod;
}void solve()
{int n,d;cin>>n>>d;init(n);vector<int>a(n+1);map<int,int>cnt;forr(i,1,n){cin>>a[i];cnt[a[i]]++;}sort(a.begin()+1,a.end());int ans=1;forr(i,1,n){int pos=lower_bound(a.begin()+1,a.end(),a[i]-d)-a.begin();int dis=i-pos+1;//可以插入的位置个数 //只看i前面的，因为往后面插也相当于后面的数往前面插 这部分在后面计算了(ans*=dis%mod)%=mod;}for(auto [x,c]:cnt){if(c>1)(ans*=ifac[c])%=mod;}cout<<ans<<endl;
}