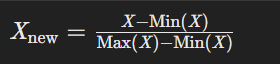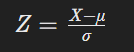1. 核心公式对比
| 标准化方法 | 计算公式 | 关键参数 |
|---|
| Min-Max标准化 | 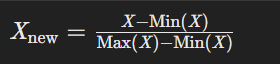
| 最小值、最大值 |
| Z-score标准化 | 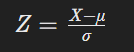
| 均值(μ)、标准差(σ) |
2. 核心区别
(1) 数据分布影响
| 维度 | Min-Max标准化 | Z-score标准化 |
|---|
| 输出范围 | 固定到 [0, 1] 或自定义范围(如[-1,1]) | 无固定范围(可能超出[-3,3]) |
| 极值敏感性 | 对异常值敏感(极大/小值直接影响分母) | 对异常值鲁棒性强 |
| 分布形状 | 保持原始分布形状 | 转换为均值为0、标准差1的分布 |
示例:
假设原始数据 [1, 2, 3, 100](100是异常值):
- Min-Max结果:
[0, 0.01, 0.02, 1](异常值导致其他数据被压缩接近0) - Z-score结果:
[-0.68, -0.66, -0.64, 1.98](异常值影响较小)
(2) 数学性质
| 性质 | Min-Max标准化 | Z-score标准化 |
|---|
| 均值 | 无固定均值 | 转换后均值=0 |
| 标准差 | 无固定标准差 | 转换后标准差=1 |
| 线性变换 | 是(等比缩放+平移) | 是(平移+缩放) |
3. 应用场景对比
| 场景 | 推荐方法 | 原因 |
|---|
| 图像处理(像素归一化) | Min-Max | 需固定到[0,1]或[0,255]范围 |
| 机器学习(SVM、KNN) | Min-Max | 基于距离的算法需要统一量纲 |
| 统计分析(假设检验) | Z-score | 便于比较不同分布的数据(如考试分数与身高) |
| 存在异常值的数据 | Z-score | 避免极值对标准化结果的扭曲 |
| 深度学习(神经网络输入) | 两者均可 | Min-Max更常见,但Z-score对ReLU激活函数更友好 |
5. 优缺点总结
| 方法 | 优点 | 缺点 |
|---|
| Min-Max | 结果直观,范围固定 | 受异常值影响大 |
| Z-score | 保留数据分布特性,兼容异常值 | 结果范围不固定,解释性稍弱 |
6. 如何选择?
- 选 Min-Max 如果:
- 需要严格限定范围(如RGB像素值)
- 数据分布均匀且无极端异常值
- 选 Z-score 如果:
- 数据存在潜在异常值
- 需要与其他数据集进行分布比较(如不同单位的指标)
特殊技巧:对异常值较多的数据,可先用IQR剔除异常值后再Min-Max标准化。